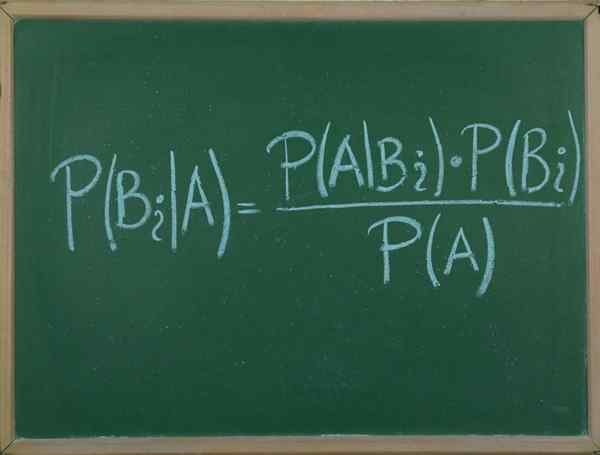Bayesov teorem
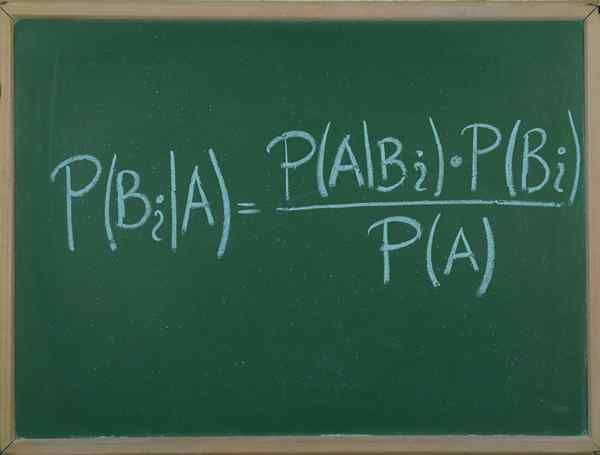
- 1002
- 36
- Don Nitzsche
Pojasnjujemo, kaj je Bayesov teorem, njegove aplikacije in uredimo vaje
Kaj je Bayesov teorem?
On Bayesov teorem To je postopek, ki nam omogoča, da izražamo pogojno verjetnost naključnega dogodka B kocke B v smislu verjetnosti porazdelitve dogodka B in verjetnosti porazdelitve samo do.
Ta teorem je zelo koristen, saj lahko zahvaljujoč temu povežemo verjetnost, da se dogodek A zgodi, vedoč, da se B dogaja, z verjetnostjo, da se zgodi nasprotno.
Bayesov teorem je bil srebrni predlog velečasnega Thomasa Bayesa, angleškega teologa iz osemnajstega stoletja, ki je bil tudi matematik. Bil je avtor več delovnih mest v teologiji, trenutno pa je znan po nekaj matematičnih pogodbah, med katerimi je Bayesov teorem že omenjen kot glavni rezultat.
Bayes se je s tem teoremom ukvarjal v delu z naslovom "esej o reševanju problema v nauku o možnostih" (esej za reševanje problema v doktrini možnosti), objavljenega leta 1763, in na katerem so velike študije razvijale študije s aplikacijami na različnih področjih znanja.
Pojasnilo
Prvič, za večje stiskanje tega izrek so potrebni nekateri osnovni pojmi teorije verjetnosti, zlasti teorem množenja za pogojno verjetnost, ki to določa
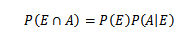
Za E in za poljubne dogodke vzorčnega prostora.
In definicijo particij, ki nam pove, da imamo1 ,Do2,…, Don Dogodki vzorčnega prostora, ti bodo tvorili particijo S, če bo aYo Medsebojno izključujejo in njihova zveza je.
Vam lahko služi: za kaj so številke? 8 glavnih uporabeČe ima to, naj bo to še en dogodek. Tako lahko vidimo B kot
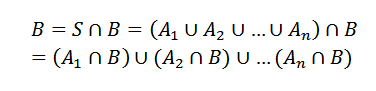
KjeYo Sekani z B so medsebojno izključujoči dogodki.
In posledično,
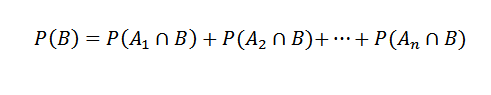
Nato uporaba teorema o množenju
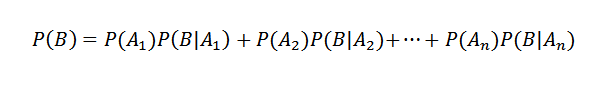
Po drugi strani je pogojna verjetnost AI B opredeljena
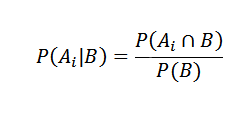
Če pravilno zamenjamo, to imamo za katero koli i
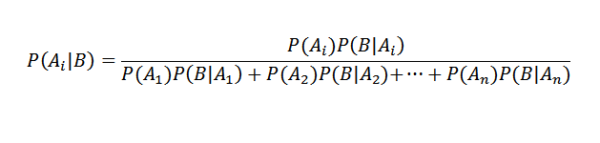
Bayesove teoremske aplikacije
Zahvaljujoč temu rezultatu so raziskovalne skupine in raznolike korporacije uspele izboljšati sisteme, ki temeljijo na znanju.
Študija bolezni
Na primer, v preučevanju bolezni lahko Bayesova teorema pomaga razbrati verjetnost, da bo bolezen našli v skupini ljudi z dano značilnostjo, pri čemer je za podatke v obeh globalnih stopnjah bolezni in prevlado omenjenih značilnosti v obeh Zdravi in bolni ljudje.
Razvoj programske opreme
Po drugi strani je v svetu visokih tehnologij vplivala na velika podjetja, ki so se zaradi tega rezultata razvila programska oprema, ki temelji na znanju ".
Kot dnevni primer imamo pomočnika Microsoft Office. Teorem Bayesa pomaga programski opremi pri oceni težav, ki jih uporabnik predstavlja, in določi, kakšen nasvet mora zagotoviti, in s tem lahko ponudite boljšo storitev v skladu z uporabnikovimi navadami.
Treba je opozoriti, da je bila ta formula do zadnjega časa prezrta, to je predvsem zato, ker je bil ta rezultat pred 200 leti razvita. Vendar pa so v našem času znanstveniki dosegli načine, kako ta rezultat uresničiti.
Rešene vaje
Vaja 1
Podjetje za mobilni telefon ima dva stroja A in B. 54% mobilnih telefonov izdeluje stroj A, ostalo pa s strojem B. Niso vsi mobilni telefoni v dobrem stanju.
Vam lahko služi: faktorizacijaDelež pokvarjenih mobilnih telefonov, ki jih je ustvaril A, je 0.2 in za b je 0.5. Kakšna je verjetnost, da je mobilni telefon omenjene tovarne pokvarjen? Kakšna je verjetnost, da, če vemo, da je mobilni telefon okvarjen, prihaja iz stroja do?
Rešitev
Tu imate eksperiment, ki se izvaja v dveh delih; V prvem delu se dogodki pojavijo:
Na: Mobilni telefon, ki ga je izdelal stroj a.
B: mobilni telefon, ki ga je izdelal stroj B.
Ker stroj A proizvede 54% mobilnih telefonov, ostalo pa proizvaja stroj B, mora stroj B proizvesti 46% mobilnih telefonov. Podane so možnosti teh dogodkov, in sicer:
P (a) = 0,54.
P (b) = 0,46.
Dogodki drugega dela eksperimenta so:
D: okvarjen mobilni telefon.
E: Ne -defektivna celica.
Kot je navedeno v izjavi, so verjetnosti teh dogodkov odvisne od rezultata, pridobljenega v prvem delu:
P (d | a) = 0.2.
P (d | b) = 0,5.
S temi vrednostmi lahko določite tudi verjetnost dodatkov teh dogodkov, to je:
P (e | a) = 1 - p (d | a)
= 1 - 0,2
= 0,8
in
P (e | b) = 1 - p (d | b)
= 1 - 0,5
= 0,5.
Zdaj je dogodek D mogoče zapisati na naslednji način:
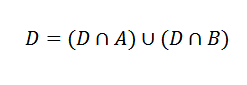 Ti dogodki so medsebojno izključujoči.
Ti dogodki so medsebojno izključujoči.
Uporaba teorema množenja za pogojno verjetnost je:
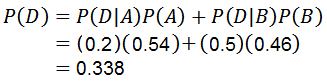
S katerim se odgovori na prvo vprašanje.
Zdaj moramo samo izračunati P (a | d), za katerega se uporablja Bayesov teorem:
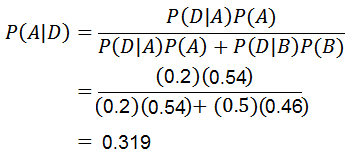
Zahvaljujoč Bayesovemu teoremu je mogoče potrditi, da je verjetnost, da je mobilni telefon izdelal stroj A, vedoč, da je mobilni telefon okvarjen, 0.319.
Vam lahko služi: icosagonoVaja 2
Tri škatle vsebujejo črno in črno kroglico. Sestava vsakega od njih je naslednja: U1 = 3b, 1n, u2 = 2b, 2n, u3 = 1b, 3n.
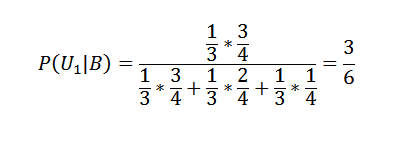
Iz njega izvlečemo naključno izbrano eno od škatel in naključna kroglica, ki se izkaže za belo. Kakšna je škatla z najverjetnejšo izbrano?
Rešitev
Preko U1, U2 in U3 bomo zastopali tudi izbrano polje.
Ti dogodki predstavljajo delitev S in preverjeno je, da je p (u1) = p (u2) = p (u3) = 1/3, ker je izbira polja naključna.
Če je B = izvlečena kroglica je bela, bomo imeli p (b | u1) = 3/4, p (b | u2) = 2/4, p (b | u3) = 1/4 .
Kar želimo pridobiti, je verjetnost, da je bila žoga odvzeta iz iu škatle, saj ve, da je ta žoga bela, torej p (ui | b), in videti, katera od treh vrednosti je bila najvišja vedeti, katera je najvišja od tega je večja verjetnost, da bo črpala belo kroglico.
Uporaba Bayesovega teorema na prvo od škatlic:
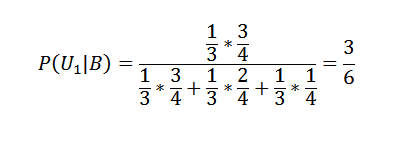
In za druga dva:
P (u2 | b) = 2/6 in p (u3 | b) = 1/6.
Nato je prva od škatlic tista, ki ima večjo verjetnost, da je bil izbran za ekstrakcijo bele kroglice.