Zgodovina, značilnosti inferencialne statistike, za kaj je, primeri

The Inferencialna statistika ali deduktivna statistika je tista, ki sklepa značilnosti populacije iz vzorcev, pridobljenih iz nje, z vrsto analiznih tehnik. S pridobljenimi informacijami se oblikujejo modeli, ki nato omogočajo napovedi o vedenju omenjene populacije.

Zato so inferencialne statistike postale najpomembnejša znanost, ki ponuja prehrano in instrumente, ki jih nešteto disciplin zahtevajo pri sprejemanju odločitev.

Fizika, kemija, biologija, inženiring in družboslovje, nenehno izkoriščajo ta orodja, ko ustvarjajo svoje modele ter oblikujejo in izvajajo eksperimente.

[TOC]

Kratka zgodovina inferencialne statistike

Statistični podatki so se pojavili v starih časih zaradi potrebe ljudi, da organizirajo stvari in optimizirajo vire. Pred izumom pisanja so bili izvedeni zapisi o številu ljudi in živine s simboli, ki so bili posneti v kamnu.

Kasneje so kitajski, babilonski in egipčanski vladarji pustili podatke o količini pridelkov in številu prebivalcev, zabeleženih na glinenih tablicah, stolpcih in spomenikih.

Rimsko cesarstvo

Ko je Rim izvajal svojo domeno v Sredozemlju, je bilo običajno, da oblasti izvajajo popise vsakih pet let. Pravzaprav beseda "statistična" izvira iz italijanske besede statista, Kaj pomeni izraziti.

Vzporedno so v Ameriki veliki predkolumbijski imperiji prinesli tudi podobne zapise.

Srednja leta

V srednjem veku so vlade v Evropi in Cerkev zabeležile last Zemlje. Potem so storili enako z rojstvom, krstimi, porokami in smrtjo.

Moderna starost

Angleški statistika John Graunt (1620-1674) je prvi napovedal na podlagi takšnih seznamov, na primer, koliko ljudi bi lahko umrlo zaradi nekaterih bolezni in ocenjenega deleža rojstev žensk in moških. Zato se upošteva oče demografije.

Sodobna starost

Pozneje je s teorijo o prihodnosti verjetnosti statistika prenehala biti zgolj zbirka organizacijskih tehnik in dosegla nepričakovano področje kot napovedna znanost.

Tako so bili sposobni strokovnjaki.

Značilnosti

Spodaj imamo najpomembnejše značilnosti te veje statistike:

- Inferencialna statistika Študij populacije, ki jo jemlje reprezentativni vzorec.

- Izbira vzorca se izvaja z različnimi postopki, pri čemer je najprimernejši tisti, ki sestavni deli naključno izberejo komponente. Tako ima kateri koli element populacije enako verjetnost, da bo izbran in z njim se izognemo neželenim pristranskosti.

Vam lahko služi: kako pretvoriti iz km/h a m/s? Rešene vaje

- Za organizacijo zbranih informacij uporablja opisne statistike.

- Na vzorcu se izračunajo statistične spremenljivke, ki služijo za oceno lastnosti populacije.

- Inferencialna ali deduktivna statistika uporablja teorijo verjetnosti za preučevanje naključnih dogodkov, to je tisti, ki nastajajo na srečo. Vsak dogodek je dodeljen določena verjetnost pojavljanja.

- Graditi hipoteze - postavitve - o parametrih populacije in jih primerjajo, da vedo, ali so pravilne ali ne, in izračuna tudi stopnjo zaupanja odziva, to je, da ponuja mero napake. Pokliče se prvi postopek Preskusi hipotez, Medtem ko je meja napake interval zaupanja.

Kaj je opisna statistika za? Prijave

Inferencialna statistika: bistvenega pomena pri sprejemanju odločitev in nadzoru kakovosti

Študij v celoti bi lahko prebivalstvo zahteval veliko sredstev v denarju, času in trudu. Zaželeno je vzeti reprezentativne vzorce, ki so veliko bolj obvladljivi, zbirajo podatke in ustvarite hipoteze ali predpostavke o vedenju vzorca.

Ko so vzpostavljene hipoteze in je njihova veljavnost kontrastna, se rezultati razširijo na populacijo in se uporabljajo za sprejemanje odločitev.

Prav tako pomagajo ustvariti modele te populacije, za prihodnje projekcije. Zato je inferencialna statistika zelo uporabna znanost za:

Sociologije in demografske študije

To so idealna polja za uporabo, saj veljajo statistične tehnike z idejo o vzpostavitvi različnih modelov človeškega vedenja. Nekaj, kar je a priori, je precej zapleteno, saj številne spremenljivke posredujejo.

V politiki se v času volitev veliko uporablja za poznavanje tendence volilnih skupin, na ta način pa stranke oblikujejo strategije.

Inženiring

Inferencialne statistične metode se pogosto uporabljajo pri inženirstvu, najpomembnejše aplikacije pa so na primer optimizacija nadzora kakovosti in procesov, ki izboljšajo čas pri izvajanju nalog, pa tudi pri preprečevanju poklicnih nesreč.

Gospodarstvo in poslovna uprava 

Z deduktivnimi metodami je mogoče izvesti projekcije o delovanju podjetja, pričakovani ravni prodaje in pomoči pri sprejemanju odločitev.

Na primer, vaše tehnike lahko uporabite za oceno reakcije kupcev na nov izdelek, ki se bliža lansiranju na trg.

Služi tudi za oceno, kakšne so spremembe v potrošniških navadah ljudi, glede na pomembne dogodke, kot je kovidna epidemija.

Primeri inferencialne statistike

Primer 1

Preprost deduktivni statistični problem je naslednji: učitelj matematike je zadolžen za 5 odsekov osnovne algebre na univerzi in se odloči, da bo uporabil povprečne zapise enega od svojih odsekov za oceno povprečja vseh vseh.

Vam lahko služi: Približno merjenje amorfnih številk: Primer in vadbaKljub temu, da je veliko populacijo mogoče preučiti s pomočjo reprezentativnega vzorca. Vir: Pixabay.

Druga možnost je, da vzamemo vzorec vsakega oddelka, preučimo njegove značilnosti in razširimo rezultate na vse odseke.

Primer 2

Vodja trgovine z oblačili za dame želi vedeti, koliko bo določena bluza prodala v poletni sezoni. Če želite to narediti, analizirajte prodajo oblačil v prvih dveh tednih sezone in tako določite trend.

Osnovni koncepti v inferencialni statistiki

Obstaja več ključnih konceptov, vključno s tistimi, ki izhajajo iz teorije verjetnosti, ki je potrebna za razumevanje vsega obsega teh tehnik. Nekateri kot populacija in vzorec smo že omenili v celotnem besedilu.

Dogodek

Dogodek ali dogodek je nekaj, kar se zgodi in ima lahko več rezultatov. Primer dogodka je lahko za zagon valute in obstajata dva možna rezultata: obraz ali pečat.

Vzorčni prostor

Je nabor vseh možnih rezultatov dogodka.

Populacija in vzorec

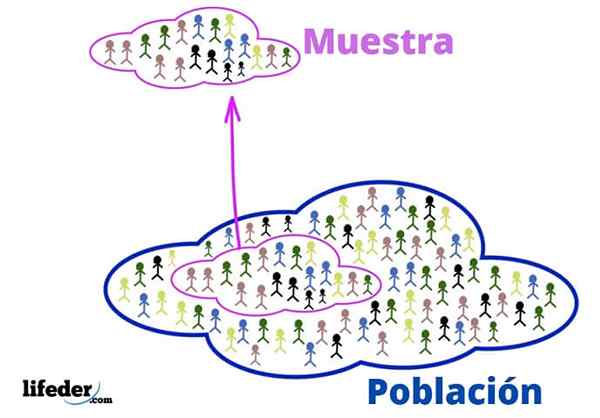Populacija in vzorec

Populacija je vesolje za študij. Ni nujno, da živijo ljudje ali bitja, saj lahko prebivalstvo v statistiki sestavljajo predmeti ali ideje.

Vzorec je vzorec podskupine populacije, ki ga iz njega skrbno izvlečejo, da je reprezentativen.

Vzorčenje

To je niz tehnik, skozi katere je izbran vzorec iz določene populacije. Vzorčenje je lahko naključno, če se za izbiro vzorca uporabljajo verjetnostne metode ali ne verjetno, če ima analitik lastno merilo izbire, glede na njihove izkušnje.

Statistične spremenljivke

Nabor vrednosti, ki imajo lahko značilnosti populacije. So razvrščeni na več načinov, na primer so lahko diskretni ali neprekinjeni. Tudi glede na svojo naravo so lahko kvalitativni ali kvantitativni.

Verjetnostne porazdelitve

Verjetnostne funkcije, ki opisujejo obnašanje velikega števila sistemov in situacij, ki jih opazimo v naravi. Najbolj znana sta Gaussova distribucija ali Gaussova in binomna porazdelitev.

Parametri in statistika 

Teorija ocene ugotavlja, da obstaja povezava med vrednostmi populacije in vrednostmi vzorca, odvzetega iz tega populacije. The parametri To so značilnosti prebivalstva, ki jih ne poznamo, vendar želimo oceniti: na primer povprečje in standardni odklon.

Svoje strani statistično so značilnosti vzorca, na primer njegov povprečni in standardni odklon.

Kot primer predpostavimo, da prebivalstvo sestavlja vse mlade, med 17 in 30 let skupnosti, in želi vedeti delež tistih, ki so trenutno v visokem šolstvu. To bi bil parameter prebivalstva, ki ga je treba določiti.

Vam lahko služi: linearna interpolacija

Za oceno je izbran naključni vzorec 50 mladih in izračuna se delež, ki študira na univerzi ali inštitutu za visoko šolstvo. Ta delež je statistika.

Če je študija izvedena, se ugotovi, da je 63 % od 50 mladih študij višje, to je populacija, narejena iz vzorca.

To je le primer, kaj lahko naredi inferencialna statistika. Znana je kot ocena, obstajajo pa tudi tehnike za napovedovanje statističnih spremenljivk in sprejemanje odločitev.

Statistična hipoteza

Gre za domnevo, ki je narejena glede vrednosti povprečja in standardnega odklona nekaterih značilnosti populacije. Če je populacija v celoti preučena, so to neznane vrednosti.

Preskusi hipotez

So predpostavke o parametrih prebivalstva veljavne? Če želite vedeti, je preverjeno, ali jih rezultati iz vzorca podpirajo ali ne, zato je treba oblikovati teste hipotez.

To so splošni koraki za izvedbo:

Korak 1

Določiti vrsto porazdelitve, ki naj bi se populacija upoštevala.

2. korak

Dve hipotezi, označeni kot h_tudi in h₁. Prva je ničelna hipoteza v katerem domnevamo, da ima parameter določeno vrednost. Drugi je Alternativna hipoteza kar je drugačna vrednost od ničelne hipoteze. Če je to zavrnjeno, je alternativna hipoteza sprejeta.

Korak 3

Vzpostavite sprejemljivo mejo za razliko med parametrom in statistiko. Redko bodo enaki, čeprav naj bi bili zelo blizu.

4. korak

Predlagajte merilo za sprejemanje ali zavrnitev ničelne hipoteze. Za to se uporablja testna statistika, ki je lahko povprečje. Če je povprečna vrednost v določenih mejah, je ničelna hipoteza sprejeta, sicer je zavrnjena.

5. korak

Kot zadnji korak je odločeno, ali je sprejeti ničelna hipoteza ali ne.

Teme, ki jih zanimajo

Podružnice statistike.

Statistične spremenljivke.

Populacija in vzorec.

Opisna statistika.

Reference

1. Berenson, m. 1985.Statistika za administracijo in gospodarstvo, koncepte in aplikacije. Interameriški uvodnik.
2. Canavos, g. 1988. Verjetnost in statistika: aplikacije in metode. McGraw Hill.
3. Devore, j. 2012. Verjetnost in statistika za inženirstvo in znanost. 8. Izdaja. Cengage učenje.
4. Zgodovina statistike. Okreval od: eumed.mreža.
5. Ibañez, str. 2010. Matematika II. Pristop kompetenc. Cengage učenje.
6. Levin, r. 1981. Statistika za skrbnike. Dvorana Prentice.
7. Walpole, r. 2007. Verjetnost in statistika za inženirstvo in znanost. Pearson.