Formule in enačbe napak vzorčenja, izračun, primeri
- 4397
- 545
- Dexter Koch
On Napaka vzorčenja tudi vzorčna napaka V statistiki je razlika med povprečno vrednostjo vzorca glede na povprečno vrednost celotne populacije. Za ponazoritev ideje si predstavljajmo, da je skupno prebivalstvo mesta milijon, od katerega želite njene povprečne čevlje, za katere se na naključnemu vzorcu vzame tisoč ljudi.
Povprečna velikost, ki izhaja iz vzorca. Ta razlika med povprečno vrednostjo vzorca in celotno populacijo je napaka vzorca.
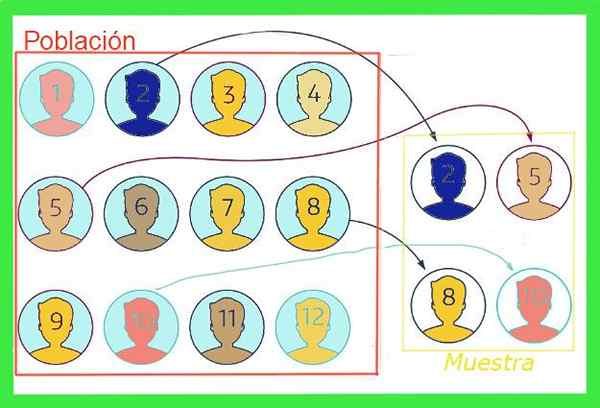
 Slika 1. Ker je vzorec podmnožica celotne populacije, ima povprečje vzorca stopnjo napake. Vir: f. Zapata.
Slika 1. Ker je vzorec podmnožica celotne populacije, ima povprečje vzorca stopnjo napake. Vir: f. Zapata. Na splošno povprečna vrednost celotne populacije ni znana, vendar obstajajo tehnike za zmanjšanje takšnih napak in formul za oceno Vzorčna stopnja napake to bo razstavljeno v tem članku.
[TOC]
Formule in enačbe
Vstavimo, da želite vedeti povprečno vrednost določene merljive funkcije x V populaciji velikosti N, ampak kako N Veliko število ni mogoče preučiti celotne populacije, zato nadaljujemo Aleatorski vzorec velikosti n<
Povprečna vrednost vzorca je označena z in povprečna vrednost celotne populacije označuje za grško pismo μ (bere Mu ali miu).
Recimo, da so vzeti m Skupni vzorci prebivalstva N, Vse enake velikosti n S povprečnimi vrednostmi
Te povprečne vrednosti ne bodo enake drug drugemu in bodo vse okoli povprečne vrednosti populacije μ. On Vzorčna stopnja napake E kaže na pričakovano ločitev povprečnih vrednosti glede na Povprečna vrednost populacije μ v določenem odstotku, imenovanem Raven zaupanja γ (Gama).
Vam lahko služi: aditiv inverznoOn Standardna stopnja napak ε vzorca velikosti n je:
ε = σ/√n
kje σ je standardni odklon (Kvadratni koren variance), ki se izračuna z naslednjo formulo:
σ = √ [(x -)2/(N - 1)]
Pomen Standardna stopnja napak ε je naslednje:
On srednja vrednost pridobljeno z vzorcem velikosti n se razume v intervalu ( - ε, + ε) z stopnja zaupanja 68,3%.
Kako izračunati napako vzorčenja
V prejšnjem razdelku je bila dana formula za iskanje Območje napak standardno vzorca N, kjer standardna beseda kaže, da gre za napako s 68 -odstotno samozavestjo.
To kaže, da če bi bili vzeti veliko vzorcev iste velikosti n, 68% jih bo dalo povprečne vrednosti v območju [ - ε, + ε].
Obstaja preprosto pravilo, imenovano Pravilo 68-95-99.7 ki nam omogoča, da najdemo rob vzorčna napaka e Za stopnje zaupanja 68%, 95% in 99,7% enostavno, saj je ta marža 1⋅ε, 2⋅ε in 3⋅ε oziroma.
Za raven zaupanja γ
Če on Raven zaupanja γ Ni nič od zgoraj navedenega, zato je napaka vzorčenja standardni odklon σ pomnožen s faktorjem Zγ, ki je pridobljen z naslednjim postopkom:
1.- Najprej raven pomembnosti α ki se izračuna iz Raven zaupanja γ Skozi naslednje razmerje: α = 1 - γ
Vam lahko služi: Bayesovi teorem2.- Potem morate izračunati vrednost 1 - α/2 = (1 + γ)/2, ki ustreza običajni frekvenci, nabrani med -∞ in Zγ, V normalni ali Gaussovi porazdelitvi je bil tipiziran f (z), katerega definicijo je mogoče videti na sliki 2.
3.- Enačba je rešena F (zγ) = 1 - α/2 Prek običajnih tabel za porazdelitev (nakopičene) F, o prek računalniške aplikacije, ki ima tipizirano inverzno Gaussovo funkcijo F-1.
V zadnjem primeru imate:
Zγ = g-1(1 - α/2).
4.- Končno se uporabi ta formula za napako vzorčenja s stopnjo zanesljivosti γ:
E = zγ⋅(σ/√n)
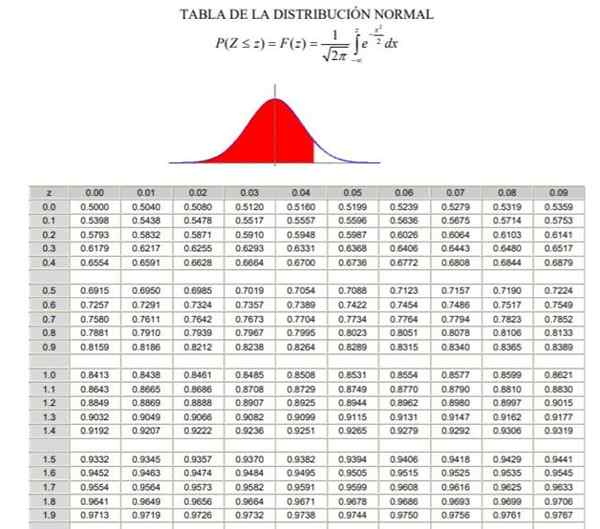 Slika 2. NORMALNA TABELA DISIČA. Vir: Wikimedia Commons.
Slika 2. NORMALNA TABELA DISIČA. Vir: Wikimedia Commons. Primeri
- Primer 1
Izračunajte Standardna stopnja napak Na povprečni teži vzorca 100 novorojenčkov. Izračun povprečne teže je bil = 3.100 kg s standardnim odklonom σ = 1.500 kg.
Rešitev
On Standardna stopnja napak je ε = σ/√n = (1500 kg)/√100 = 0,15 kg. Kar pomeni, da je s temi podatki mogoče sklepati, da je teža 68% novorojenčkov med 2.950 kg in 3.25 kg.
- Primer 2
Določiti meja vzorčne napake in in razpon teže 100 novorojenčkov z 95 -odstotno stopnjo zaupanja, če je povprečna teža 3.100 kg s standardnim odklonom σ = 1.500 kg.
Rešitev
Če Pravilo 68; 95; 99.7 → 1⋅ε; 2⋅ε; 3⋅ε, Imaš:
E = 2⋅ε = 2⋅0,15 kg = 0,30 kg
Z drugimi besedami, 95% novorojenčkov bo imelo pesos med 2800 kg in 3.400 kg.
- Primer 3
Določite obseg novorojenčkov iz primera 1 z 99,7 -odstotno maržo zaupanja.
Vam lahko služi: Rhomboid: značilnosti, kako odnesti obod in območjeRešitev
Napaka vzorca z 99,7% zaupanja je 3 σ/√n, To je za naš primer E = 3 *0,15 kg = 0,45 kg. Od tu je sklepano, da bo 99,7% novorojenčkov imelo pesos med 2.650 kg in 3.550 kg.
- Primer 4
Določite faktor Zγ Za stopnjo zanesljivosti 75%. Določite stopnjo napake vzorčenja s to stopnjo zanesljivosti za primer, postavljeno v primer 1.
Rešitev
On stopnja zaupanja je γ = 75% = 0,75, ki se nanaša na raven pomembnosti α skozi odnos γ= (1 - α), tako da je stopnja pomembnosti α = 1 - 0,75 = 0,25.
To pomeni, da je nakopičena normalna verjetnost med -∞ in Zγ je:
P (z ≤ Zγ ) = 1 - 0,125 = 0,875
Kaj ustreza vrednosti Zγ od 1.1503, kot je prikazano na sliki 3.
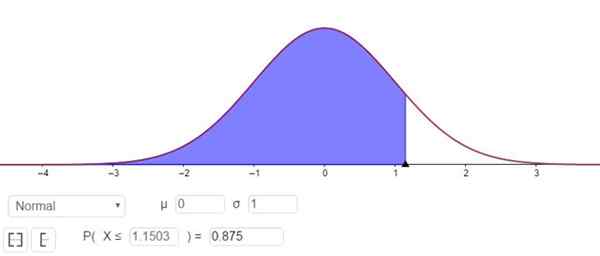 Slika 3. Določitev faktorja Zγ, ki ustreza 75 -odstotni stopnji zaupanja. Vir: f. Zapata skozi Geogebro.
Slika 3. Določitev faktorja Zγ, ki ustreza 75 -odstotni stopnji zaupanja. Vir: f. Zapata skozi Geogebro. Z drugimi besedami, napaka vzorčenja je E = zγ⋅(σ/√n)= 1.15⋅(σ/√n).
Ko se uporabi za primer 1, daje napako:
E = 1,15*0,15 kg = 0,17 kg
S 75 -odstotno stopnjo zaupanja.
- Vaja 5
Kakšna je raven zaupanja, če je zα/2 = 2.4 ?
Rešitev
P (z ≤ zα/2 ) = 1 - α/2
P (z ≤ 2.4) = 1 - α/2 = 0,9918 → α/2 = 1 - 0,9918 = 0,0082 → α = 0,0164
Raven pomembnosti je:
α = 0,0164 = 1,64%
In končno ostaja raven zaupanja:
1- α = 1 - 0,0164 = 100% - 1,64% = 98,36%
Reference
- Canavos, g. 1988. Verjetnost in statistika: aplikacije in metode. McGraw Hill.
- Devore, j. 2012. Verjetnost in statistika za inženirstvo in znanost. 8. Izdaja. Cengage.
- Levin, r. 1988. Statistika za skrbnike. 2. mesto. Izdaja. Dvorana Prentice.
- Sudman, s.1982. Vprašanja: Praktični vodnik za oblikovanje vprašalnika. San Francisco. Jossey Bass.
- Walpole, r. 2007. Verjetnost in statistika za inženirstvo in znanost. Pearson.
- Wonnacott, t.H. in r.J. Wonnacott. 1990. Uvodna statistika. 5. izd. Wiley
- Wikipedija. Vzorčna napaka. Pridobljeno iz: v.Wikipedija.com
- Wikipedija. Meja napak. Pridobljeno iz: v.Wikipedija.com
- « Zgodovina, značilnosti inferencialne statistike, za kaj je, primeri
- U -test od Manna - Whitney Kaj je in kadar velja, izvedba, primer »

