Opisna statistika Zgodovina, značilnosti, primeri, koncepti

The Opisna statistika To je veja statistike, ki obravnava zbiranje in organiziranje informacij o vedenju sistemov s številnimi elementi, splošno znano kot ime prebivalstvo.

Za to uporablja numerične in grafične tehnike, skozi katere predstavlja informacije, ne da bi napovedoval ali sklepal o populaciji, kjer pride.

Opisna statistika se šteje za organiziranje in predstavitev informacij priročno

[TOC]

Zgodovina

Stara leta

Statistika izvira iz človeške potrebe, da organizira potrebne informacije za svoje preživetje in dobro počutje, pa tudi za zagotavljanje dogodkov, ki vplivajo. Velike civilizacije antike so pustile evidence naseljencev, zbranih davkov, znesek pridelkov in velikost vojsk.

Na primer, med dolgim ​​vladanjem Ramses II (1279-1213 do.C) je naročil popis zemlje in prebivalcev v Egiptu, ki je do takrat imel približno 2 milijona prebivalcev.

Prav tako je Biblija, da je Mojzes izvedla popis, da bi vedela, koliko vojakov ima dvanajst plemen Izraela.

Tudi v starodavni Grčiji so bile narejene števila ljudi in virov. Rimljani, ki so bili znani po svoji visoki organizaciji, so občasno registrirali prebivalstvo in vsakih pet let pripravljali popise, vključno z ozemlji in viri.

Renesansa

Po upadu Rima so se pomembni statistični zapisi prestrašili, do prihoda renesanse, ko se statistika ponovno pojavi.

Kulminirala v sedemnajstem stoletju se je rodila teorija verjetnosti, rezultat naklona ljudi za igre na srečo, ki je statistiki zagotovila matematično strogost, ki je postala sama po sebi znanost.

Moderna starost

Nov impulz je prišel s teorijo napak in minimalnih kvadratov v devetnajstem stoletju, ki je sledil metodi korelacije med spremenljivkami, da bi kvantitativno ocenili razmerje med njimi.

Do konca, v dvajsetem stoletju se je statistika razširila na vsako vejo znanosti in inženiringa kot nepogrešljivo orodje pri reševanju problemov.

Značilnosti opisne statistike

Za opisne statistike je značilno:

- Organizirajte informacije, zbrane v podatkih in grafiki. Grafi so lahko raznoliki: histogrami, frekvenčni poligoni, diagrami v obliki torte, med drugim.

- Razdelite podatke v frekvenčnih območjih, da olajšajo njihovo upravljanje. Uporabite aritmetiko, da poiščete najbolj reprezentativne vrednosti podatkov s pomočjo ukrepov osrednje tendence, pa tudi analizirajte le.

- Določite obliko distribucij, njihovo simetrijo, če so osredotočene ali pristranske, in če so usmerjene ali bolje rečeno.

Vam lahko služi: implicitni derivati: kako so rešeni in rešeni vaje

Kaj je opisna statistika za?

Kadar koli je potrebno.

Nato omenimo nekaj primerov:

Ekonomija

Opisna statistika obravnava registracijo in organiziranje podatkov o populacijah in njihovi starosti, dohodku, naložbah, dobičku in odhodkih. Na ta način vlade in institucije načrtujejo izboljšave in ustrezno vlagajo.

S pomočjo vaše pomoči spremljajte nakupe, prodajo, donose in učinkovitost storitev. Zaradi tega so statistični podatki nepogrešljivi pri odločanju.

Fizika in mehanska

Fizika in mehanika uporabljajo statistiko za preučevanje neprekinjenih medijev, ki so sestavljeni iz velikega števila delcev, kot so atomi in molekule. Izkazalo se je, da vsakega od njih ni mogoče posebej spremljati.

Toda preučevanje globalnega vedenja sistema (na primer plinski del) z makroskopskega vidika je mogoče ugotoviti povprečja in določiti makroskopske spremenljivke, da bi spoznali njegove lastnosti. Primer tega je kinetična teorija plinov.

Zdravilo

To je bistveno orodje pri spremljanju bolezni, iz njegovega izvora in v času njenega razvoja, pa tudi učinkovitost zdravljenja.

Statistični podatki, ki opisujejo stopnje obolevnosti, zdravljenja, časov inkubacije ali razvoja bolezni, starosti, v kateri se običajno pojavlja, in podatki o slogu, so potrebne pri načrtovanju najučinkovitejših načinov zdravljenja.

Prehrana

Ena od številnih aplikacij opisne statistike je registrirati in naročiti podatke o porabi hrane v različnih populacijah: njihove količine, kakovosti in ki so najbolj porabljene, med drugimi drugimi opažanji, ki zanimajo strokovnjake.

Primeri opisne statistike

Spodaj bomo videli nekaj primerov, ki ponazarjajo, kako koristna so orodja opisne statistike, ki pomagajo pri sprejemanju odločitev:

Primer 1

Za izboljšanje šolskih jedilnic so potrebne informacije o uporabnikih. Vir: Wikimedia Commons.

Izobraževalni organi za institucionalne izboljšave državnega načrta. Recimo, da bodo uvedli nov sistem šolskih jedilnic.

Za to je treba imeti podatke o študentski populaciji, na primer število učencev na razred, starost, spol, višino, težo in socialno -ekonomsko stanje. Potem so te informacije predstavljene v obliki tabel in grafov.

Primer 2

Za spremljanje lokalne nogometne reprezentance in nove podpise, menedžerji nosijo število odigranih tekem, zmagajo, izenačene in izgubljene, pa tudi število golov, strelcev in kako jim je uspelo doseči: prosti strel, s polovice sodišča, kazni, kazni, kazni, kazni, kazni, kazni, kazni, kazni, kazni, kazni z levo nogo ali desno, med drugim.

Lahko vam služi: medsebojno izključujoči dogodki: lastnosti in primeri

Primer 3

Trgovina s sladoledom ima več okusov sladoleda in želi izboljšati svojo prodajo, zato lastniki izvedejo študijo, kjer štejejo število kupcev, jih ločijo v skupine po spolu in starostnem obdobju.

V tej raziskavi so na primer zabeleženi najljubši okus sladoleda in najbolje prodajna predstavitev. In z zbranimi podatki načrtujejo nakupe okusov in potrebne posode in dodatke za njihovo pripravo.

Osnovni koncepti opisne statistike

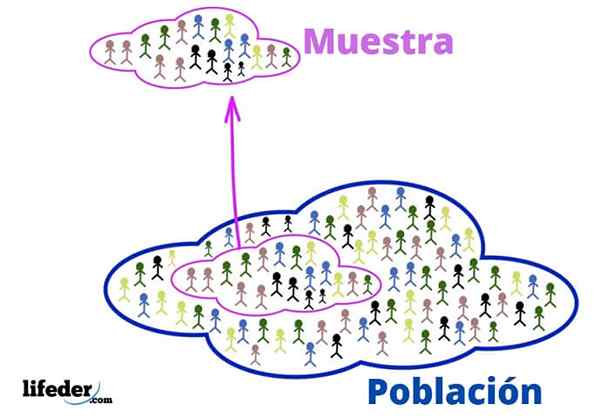Populacija in vzorec

Ti temeljni koncepti so potrebni za uporabo statističnih tehnik, poglejmo:

Prebivalstvo

V statističnem kontekstu se prebivalstvo nanaša na vesolje ali kolektiv, iz katerega prihajajo informacije.

Ne gre vedno za ljudi, saj so lahko nabori živali, rastlin ali predmetov, kot so avtomobili, atomi, molekule in celo dogodki in ideje.

Vzorec

Ko je populacija zelo velika, se iz njega izvleče reprezentativni vzorec in analizira, ne da bi izgubili ustrezne informacije.

Izbrati ga je mogoče naključno ali v skladu z nekaterimi merili, ki jih je predhodno vzpostavil analitik. Prednost je, da je podvrsta prebivalstva veliko bolj obvladljiv.

Spremenljivka

Se nanaša na niz vrednot, ki lahko sprejmejo določeno značilnost populacije. Študija lahko vsebuje različne spremenljivke, kot so starost, spol, teža, akademska raven, civilni status, dohodek, temperatura, barva, čas in še veliko več.

Spremenljivke so lahko različne narave, zato obstajajo merila za njihovo razvrščanje in njihovo najprimernejšo zdravljenje.

Kategorične spremenljivke in numerične spremenljivke

Glede na to, kako se merijo, so lahko spremenljivke:

-Kategorično

-Številčno

Kategorične spremenljivke, imenovane tudi kvalitativno, Predstavljajo lastnosti, kot je civilni status osebe, ki je lahko samska, poročena, razvezana ali vdova.

Po drugi strani do številčnih spremenljivk oz kvantitativno, Jih je mogoče izmeriti, kot so starost, čas, teža, dohodek in še več.

Grafika je zelo pomembna za predstavitev informacij, saj je na prvi pogled cenjen trend podatkov. Vir: Piqsels.

Diskretne in neprekinjene spremenljivke

Diskretne spremenljivke sprejmejo le diskretne vrednosti, kot pove že ime. Primeri jih je število otrok družine, koliko predmetov je v določenem poteku in količina avtomobilov na parkirišču.

Te spremenljivke ne sprejmejo vedno celotnih vrednosti, ker obstajajo tudi frakcije.

Po drugi strani neprekinjene spremenljivke priznavajo neskončne vrednosti v določenem območju, kot so teža osebe, pH krvi, čas telefonskega posvetovanja in premer nogometnih kroglic.

Vam lahko služi: simetrija

Ukrepi osrednje težnje

Dajte predstavo o splošnem trendu, ki ga sledijo podatki. Omenili bomo tri najbolj uporabljene centralne ukrepe:

-Polovica

-Mediana

-Moda

Polovica

Enakovredna povprečnim vrednostim. Izračuna se z dodajanjem vseh opazovanj in delitvijo med skupno število:

 Kjer x_Yo To je vsako opazovanje in n jih je skupno.

Moda

To je vrednost, ki se najbolj ponovi v naboru podatkov, najpogosteje, saj lahko v distribuciji obstaja več kot ena moda.

Mediana

Pri naročanju nabora podatkov je mediana osrednja vrednost vseh.

Ukrepi disperzije

Opozarjajo na spremenljivost podatkov in dajo predstavo o tem, kako daleč ali razpršeni so od osrednjih ukrepov. Najbolj uporabljeni so:

Domet

Je razlika med največjo vrednostjo x_M In najmanjši x_m nabora podatkov:

Domet = x_M - x_m

Odstopanje

Izmerite, kako daleč so podatki povprečne vrednosti. Za to je narejeno povprečje, vendar z razlikami med katero koli vrednostjo x_Yo in povprečje, na kvadrat, da se prepreči, da bi se medsebojno odpovedali. Običajno ga označuje grška črka σ na kvadrat ali s S²:

Standardni odklon

Varianta nima enakih enot kot podatki, zato je standardni odklon opredeljen kot kvadratni koren variance in je označen kot σ ali s:

Frekvenčne porazdelitve

Namesto če upoštevamo vsake podatke posamično, jih je bolje, da jih razvrstimo v območje, kar olajša delo, še posebej, če je veliko vrednosti. Na primer, pri delu z otroki šole jih je mogoče razvrstiti v starostne razpone: od 0 do 6 let, od 6 do 12 let in od 12 do 18 let.

Grafi

So odličen način za cenitev distribucije podatkov o pogledu in vsebujejo vse informacije, zbrane v tabelah in slikah, vendar veliko bolj dostopne.

Obstaja široko paleto: s palicami, linearnimi, krožnimi, stebli in listi, histogrami, frekvenčnimi poligoni in piktogrami. Primeri statističnih grafov so predstavljeni na sliki 3.

Teme, ki jih zanimajo

Podružnice statistike.

Statistične spremenljivke.

Populacija in vzorec.

Inferencialna statistika.

Reference

1. Faraldo, str. Statistika in metodologija raziskovanja. Okrevano od: eio.USC.je.
2. Fernández, s. 2002. Opisna statistika. 2. mesto. Izdaja. ESIC uvodnik. Obnovi se od: Google Books.
3. Zgodovina statistike. Okreval od: eumed.mreža.
4. Ibañez, str. 2010. Matematika II. Pristop kompetenc. Cengage učenje.
5. Monroy, s. 2008. Opisna statistika. 1. Izdaja. Nacionalni politehnični inštitut v Mehiki.
6. Formule vesolja. Opisna statistika. Okrevano od: univerzeformulas.com.