Redna spremenljivka

Kaj je redna spremenljivka?

Ordinatna spremenljivka je tista, ki ima vrednosti, ki jih je mogoče naročiti (ali označiti naročilo). Na primer, človekovo spremenljivko stara lahko razvrstimo med: visoko, povprečno in nizko.

Ordinalna lestvica poleg prepoznavanja, združevanja in razlikovanja študijskih enot kot nominalne spremenljivke opisuje tudi velikost in zato je značilna naročila; to pomeni, da je mogoče študijske enote vse bolj ali zmanjšuje po velikosti.

Ta lestvica govori o prvem, drugem, tretjem ali visokem, srednjem, basu; Vendar ukrep ni vzpostavljen med razredi. Na primer: spremenljivka kvalifikacije v testu zadovoljstva za zagotovljeno storitev je mogoče izmeriti v štirih kategorijah: nezadovoljni, ravnodušni, zadovoljni, zelo zadovoljni.

Naročeno ga je mogoče v skladu z manifestom, vendar ni znano, kako različno.

Naredna lestvica se nanaša na meritve, ki med zaporednimi meritvami naredijo samo "večje", "manjše" ali "enake" primerjave. Predstavlja klasifikacijo ali naročanje nabora opaženih vrednosti.

Koncept redne spremenljivke in značilnosti

Na redni lestvici se opazovanja postavljajo v relativni vrstni red glede na značilnost, ki se ocenjuje. To pomeni, da so kategorije podatkov razvrščene ali urejene glede na posebno značilnost, ki jo imajo.

Če uporabljamo številke, obseg teh predstavlja vrstni red obsega opazovanega atributa. Samo razmerja "večja od", "nižja od" in "enaka" imajo pomen na redni merilni lestvici.

Vam lahko služi: evklidska geometrija

Z matematičnega vidika in kot nazivne lestvice tudi zaporedne lestvice priznavajo izračun deleža, odstotkov in razlogov.

Osrednji ukrep tendence, ki najbolje razloži ordinalno spremenljivko, je mediana, ki je vrednost, ki se nahaja v središču nabora urejenih podatkov od najmanj do največjih.

Kadar so predmeti razvrščeni po značilnosti, je mogoče ugotoviti, kateri predmet ima bolj ali manj značilnosti v primerjavi z drugim; Vendar razlike ni mogoče količinsko ovrednotiti.

Na primer, trije predmeti, ki so bili naročeni kot "prvi", "drugi" in "tretji", ob upoštevanju katere koli značilnosti. Drugo mesto se od prvega razlikuje po znesku, ki ni nujno enak zneski, v katerem se razlikuje od tretjega mesta.

Primeri rednih spremenljivk

Nekaj ​​primerov rednih spremenljivk:

- Družbeni razred (A - visok; B - visoki mediji; C - mediji; D - nizko; E - zelo nizko).

- Kvalitativne šolske opombe (i - nezadostne; a - sprejemljivo; b - dobro; s - izjemno; e - odlično).

- Vojaške diplome (general, polkovnik, podpolkovnik, major, kapitan itd.).

- Stopnja šolanja (osnovna, srednja šola, strokovni tehnik, tehnolog, univerza itd.).

- Stopnja razvoja človeka (novorojenček, dojenček, otrok, mladi, odrasli, stari).

- Klasifikacija filmov (A - vse občinstvo; B - več kot 12 let; C - več kot 18 let; D - več kot 21 let).

- Zrelost sadja (zelena, barva, zrela, zelo zrela, gnilo).

- Stopnja zadovoljstva z zagotavljanjem javne službe. (Zelo zadovoljen; zadovoljen; ravnodušen; itd.).

Vam lahko služi: ne -združeni podatki: primeri in rešeni primeri in vaja

- Primeri pojasnili

Ocena učitelja s strani njegovih učencev

Študenti določenega tečaja lahko izpolnijo anketo za oceno pedagoške zmogljivosti učitelja, ki se meri z redno spremenljivko, katere lestvica je: 5 - odlična, 4 - dobro, 3 - povprečna, 2 - slabo, 1 - 1 - revni.

Vrednosti spremenljivke so naročene od večjega ali boljšega do manj ali slabše: odlično je boljše od dobrega, no, je boljše od povprečja itd. Vendar ni mogoče razlikovati velikosti razlik.

Je razlika med odličnim in dobrim? Ni mogoče potrditi.

Če uporabljamo številke, te ne kažejo na velikost. Na primer, ne bi smeli sklepati, da je dobra kvalifikacija (kvalifikacija 4) dvakrat višja od slabega (kvalifikacija 2). Lahko samo rečemo, da je dobra kvalifikacija boljša od slabe ocene, vendar je ni mogoče količinsko določiti, v kolikšni meri je boljše.

Stopnja sprejemanja obroka

Natečaj za degustacijo ocenjuje obroke v kuhinjskem tekmovanju skozi redno spremenljivko na ravni sprejemanja, izražene v: a - odlično, b - no, c - ni sprejemljivo. Uporaba urejenega merjenja od višje do najnižje je dokazana, vendar razlike med vrednostmi lestvice ni mogoče določiti.

Ker gre za tekmovanje, kako je odločen zmagovalec? Zdi se, da je najprimernejša uporaba mode za sprejemanje odločitve o zmagovalcu tekmovanja. Razumeti modo kot ime, ki je dana največji vrednosti (najpogostejši) štetja na ravni. Na primer, šteli so 5 a, 14 b, 10 c; Moda je B, ker je imela raven največje mnenja.

Vam lahko služi: logaritmična funkcija: lastnosti, primeri, vaje

Razlike z nazivno spremenljivko

Naslednja tabela prikazuje nekatere razlike in podobnosti med spremenljivkami, izmerjenimi v nominalnem in zaporednem obsegu:

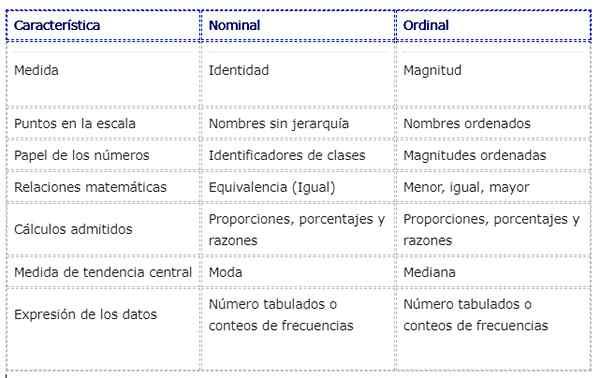
Reference

1. Freund, r.; Wilson, w.; Mohr, d. (2010). Statistične metode. Tretji ed. Academic Press-Ellevier Inc.
2. Kozarec, g.; Stanley, J. (devetnajst devetdeset šest). Statistične metode, ki se ne uporabljajo za družbene vede. Hispanoamerican Hall Hall s. Do.
3. Lepo.; Marchal, w.; Wathen, s. (2012). Statistični podatki, ki se uporabljajo za podjetja in gospodarstvo. Deseti izd. McGraw-Hill/Interamerican Editors S. Do.
4. Orlandoni, g. (2010). Statistične merilne lestvice. Revija Telos. Pridobljeno iz OJS.mesto.Edu.
5. Siegel, s.; Castellan, n. (1998). Neparametrična statistika, ki se uporablja za vede o vedenju. Četrti Ed. Uredništvo Trillas S. Do.
6. Wikipedija. (2019). Raven merjenja. Pridobljeno iz.Wikipedija.org.