Temeljni teorem aritmetične demonstracije, aplikacij, vaj

On Temeljni teorem aritmetike Navaja, da je mogoče vsako naravno število, večjo od 1.

Ne pozabite, da je glavna številka str To je tisti, ki priznava le kot pozitivne delitve in 1. Naslednje številke so bratranci: 2, 3, 5, 7, 11, 13 in tako naprej, saj obstajajo neskončni. Številka 1 se ne šteje za bratranca, ker ima en sam delitev.

Slika 1. Euclides (levo) je v svojih elementih knjig pokazal temeljni teorem aritmetike (350 a.C.), In prva popolna demonstracija je posledica Carl F. Gauss (1777-1855) (desno). Vir: Wikimedia Commons.

Njihove strani se imenujejo številke, ki ne izpolnjujejo zgoraj navedenega sestavljene številke, Kot 4, 6, 8, 9, 10, 12, 14 ... Vzemimo na primer številko 10 in takoj vidimo, da ga je mogoče razčleniti kot produkt 2 in 5:

10 = 2 × 5

Oba 2 in 5 sta res najpomembnejša številka. Teorem navaja, da je to mogoče za katero koli številko n:

Kjer p₁, str₂, str₃… P_r So glavne številke in k₁, k₂, k₃,... K_r So naravne številke. Tako da glavne številke delujejo kot opeke, iz katerih se z množenjem gradijo naravne številke.

[TOC]

Demonstracija temeljnega teorema aritmetike

Začne dokazati, da se lahko vsaka številka razgradi v glavnih dejavnikih. Biti naravna številka n> 1, bratranec ali spojina.

Na primer, če je n = 2, se lahko izrazi kot: 2 = 1 × 2, ki je bratranec. Na enak način nadaljujemo z naslednjimi številkami:

3 = 1 × 3

4 = 2 × 2

5 = 1 × 5

6 = 2 × 3

7 = 1 × 7

8 = 2 × 2 × 2

Nadaljujemo tako, razgradimo vse naravne številke, dokler ne dosežemo številke n -1. Poglejmo, ali lahko to storimo s številko, ki sledi: n.

Če je N bratranec, ga lahko razgradimo kot n = 1 × n, vendar predpostavimo, da je n sestavljen in ima delitelj d, logično manj kot n:

Vam lahko služi: opisna statistika: zgodovina, značilnosti, primeri, koncepti

1< d < n.

DA N/D = P₁, S P₁ Glavna številka, potem je n napisana kot:

n = str₁.d

Če je D bratranec, ni več za početi, če pa ni, obstaja številka n₂ ki je delitelj D in manj od tega: N₂ < d, por lo que d podrá escribirse como el producto de n₂ Za drugo številko bratranca P₂:

d = p₂ n₂

Da bi z zamenjavo v originalni številki N dal::

n = str₁ .str₂ .n₂

Zdaj predpostavimo n₂ Prav tako ni glavna številka in jo zapišemo kot izdelek glavne številke P₃, za svojega delilnika₃, takšen, da n₃ < n₂ < n₁ < n:

n₂ = p₃.n₃ → n = P₁ str₂ str₃.n₃

 Ta postopek ponovimo končno številokrat, dokler ne dobite:

n = str₁.str₂.str₃ … P_r

To pomeni, da je mogoče razčleniti vse celotne številke od 2 na število N, kot produkt glavnih številk.

Edinstvenost razgradnje pri glavnih dejavnikih

Preverimo zdaj, da je ta razgradnja, razen vrstnega reda dejavnikov, edinstven. Recimo, da lahko pišete na dva načina:

n = str₁.str₂.str₃ … P_r = q_1.q₂.q₃… Q_s  (z r ≤ s)

Seveda q₁, q₂, q₃… Tudi oni so glavne številke. Kot str₁ Razdelite na (q_1.q₂.q₃… Q_s) Nato str₁ Je enak kateri koli "q", ne glede na to Katero, torej lahko rečemo, da P₁ = q₁. Delimo n med P₁ In dobimo:

str₂.str₃ … P_r =_.q₂.q₃… Q_s

Ponovimo postopek, da vse razdelimo med P_r, Potem dobimo:

1 = q_R+1… Q_s

Vendar ni mogoče priti do Q_R+1… Q_s = 1 Ko r < s, solo si r = s. Aunque al admitir que r = s, también se admite que los “p” y los “q” son los mismos. Por lo tanto la descomposición es única.

Prijave

Kot smo že povedali, glavne številke predstavljajo, če želite, atomi števil, njihove osnovne komponente. Torej ima temeljni teorem aritmetike številne aplikacije, najbolj očitne: z velikimi številkami lahko lažje sodelujemo, če jih izrazimo kot izdelek manjših številk.

Vam lahko služi: cele številke

Na enak način najdemo največji skupni večkratnik (m.c.m.) in največji skupni delitelj (m.C.D.), Postopek, ki nam pomaga, da lažje naredimo vsote ulomkov, poiščemo korenine velikega števila ali delujemo z radikali.

Poleg tega so glavne številke izjemno enigmatične. Vzorec še ni prepoznan v njih in ni mogoče vedeti, kaj bo naslednje. Največje do trenutkov so našli računalniki in jih je 24. 24.862.048 števke, Čeprav se nove številke vsakič pojavljajo manj pogosto.

Primo številke v naravi

Cicadas, Cycaked ali Chicharras, ki živijo na severovzhodu ZDA, se pojavijo v 13 ali 17 letih ciklov. Oba sta glavne številke.

Na ta način se Chicharras izogibajo sovpadanju s plenilci ali konkurenti, ki imajo druge rojstne obdobje, niti različne sorte Chicharra ne tekmujejo med seboj, saj v istem letu ne sovpadajo.

Slika 2. Magicirana Cicada del Este iz Združenih držav Amerike se pojavi vsakih 13 ali 17 let. Vir: Pxfuel.

Primo številke in spletni nakupi

Primo številke se uporabljajo v kriptografiji za ohranitev podrobnosti kreditnih kartic, ko kupujete spletne nakupe. Na ta način podatki, ki jih kupec prispe natančno v trgovino.

Kot? Podatki o karticah so kodirani v številki N, ki jih je mogoče izraziti kot produkt glavnih številk. Te glavne številke so ključne, ki razkrivajo podatke, vendar jih javnosti niso znani, lahko jih dekodirajo le na spletu.

Razgradnja številke v dejavnike je lahka naloga, če so številke majhne (če se vaje rešijo), vendar se v tem primeru uporabljajo kot ključne številke 100 števk, kar z množenjem daje veliko večje številke, katere podrobna razgradnja pomeni a Ogromno delo.

Vam lahko služi: natančna ocena

Rešene vaje

- Vaja 1

Razgradite 1029 na glavne dejavnike.

Rešitev

1029 je deljiv s 3. Znano je, ker je z dodajanjem številk vsota večkratna od 3: 1+0+2+9 = 12. Ker vrstni red dejavnikov ne spremeni izdelka, lahko začnemo tam:

1029 3

343

1029 = 3 × 343

Na drugi strani 343 = 7³, tako:

1029 = 3 × 7³ = 3 × 7 × 7 × 7

In ker sta oba 3 in 7 glavna številka, je to razgradnja 1029.

- Vaja 2

Faktor TrinomAl x² + 42x + 432.

Rešitev

Trinomial je napisan v obliki (x+a). (x+b) in najti moramo vrednosti A in B, tako da:

A+B = 42; do.B = 432

Številka 432 se razgradi na glavne faktorje in od tam ga izbere Tanteo, ustrezna kombinacija dejstev, dodanih v 42.

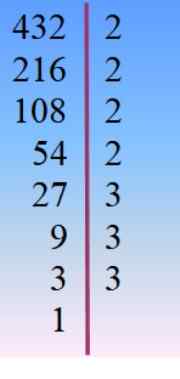
432 = 2⁴ × 3³ = 23³× 2³ = 2⁴× 3² × 3 =…

Od tu obstaja več možnosti za pisanje 432:

432 = 16 × 27 = 24 × 18 = 54 × 8 = 6 × 72… .

In vse je mogoče najti s kombiniranjem izdelkov med glavnimi dejavniki, vendar za rešitev predlagane vaje je edina ustrezna kombinacija: 432 = 24 × 18 od 24 + 18 = 42, nato:

x² + 42x + 432 = (x + 24). (x +18)

Reference

1. Baldor, a. 1986. Praktična teoretična aritmetika. Uredniško kulturno podjetje ameriških besedil s.Do.
2. BBC svet. Skriti kodeks narave. Pridobljeno iz: BBC.com.
3. Iz Leona, Manuel.Številke Primo: internetni skrbniki. Obnovi se od: blogi.20 minut.je.
4. Ne. Teorija številk I: Temeljni teorem aritmetike. Pridobljeno iz: Theoriadenemeros.Wikidot.com.
5. Wikipedija. Temeljni teorem aritmetike. Okrevano od: je.Wikipedija.org.