Teorem o obstoju in demonstraciji edinstvenosti, primeri in vaj

On Obstoj in teorem o edinstvenosti Vzpostavi potrebne in zadostne pogoje za diferencialno enačbo prvega reda z danim začetnim pogojem, da ima rešitev in da je tudi ta rešitev edina. 

Vendar teorem ne daje nobene tehnike ali navedbe, kako najti takšno rešitev. Teorem o obstoju in edinstvenosti se razširi tudi na diferencialne enačbe višjega reda z začetnimi pogoji, kar je znano kot Cauchy problem.

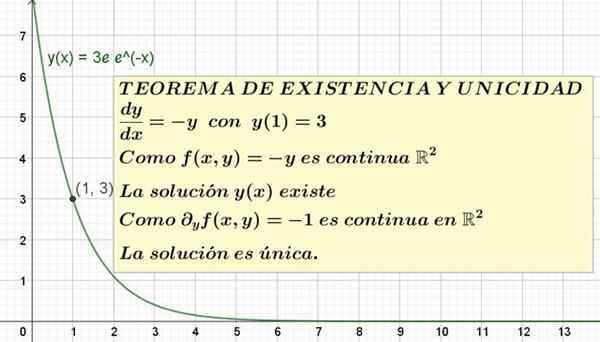
Slika 1. Prikazana je diferencialna enačba z začetnim stanjem in njegovo rešitev. Teorem o obstoju in edinstvenosti zagotavlja, da gre za edino možno rešitev.

Uradna izjava teorema obstoja in edinstvenosti je naslednja:

"Za diferencialno enačbo in '(x) = f (x, y) z začetnim stanjem in (a) = b,  obstaja Vsaj ena raztopina v pravokotnem območju ravnine Xy vsebuje točko (A, b), Ja f (x, y) V tej regiji je neprekinjeno. In če delni derivat F iz spoštovanja do in: G = ∂f/ ∂y V istem pravokotnem območju je neprekinjen, zato je rešitev edinstvena v okolju točke (A, b) vsebina v območju kontinuitete F in g."

Uporabnost tega teorema je najprej vedeti, kakšna so območja ravnine XY, v kateri je lahko rešitev, in tudi vedeti, ali je najdena rešitev edina možna ali če obstajajo druge. 

Upoštevajte, da v primeru, da je stanje edinstvenega.

[TOC]

Demonstracija teorema o obstoju in edinstvenosti

Slika 2. Charlesu Émile Picard (1856-1941) Eden prvih demonstracij teorema obstoja in edinstvenosti je akreditiran. Vir: Wikimedia Commons.

Za to teorem sta znani dve možni demonstraciji, ena od njih je demonstracija Charlesa Émile Picard (1856-1941), drugi pa Giuseppe Peano (1858-1932), ki temelji na delih Augustina Louisa Cauchyja (1789-1857 ).

Vam lahko služi: sočasni vektorji: značilnosti, primeri in vaje

Treba je opozoriti, da so pri demonstraciji tega teorema sodelovali najsvetlejši matematični um devetnajstega stoletja, zato je lahko intuit, da nobeden od njih ni preprost.

Če želite uradno pokazati teorem, je treba najprej vzpostaviti vrsto naprednejših matematičnih konceptov, kot so lipschitz funkcije, banaški prostori, karateodory in še več teorema obstoja, ki se izognejo namenu članka.

Velik del diferencialnih enačb, ki se ukvarjajo s fiziko, se ukvarjajo z neprekinjenimi funkcijami v zanimivih regijah, zato se bomo omejili na prikaz načina uporabe teorema v preprostih enačbah.

Primeri

- Primer 1

Razmislite o naslednji diferencialni enačbi z začetnim pogojem:

in '(x) = - y; z in (1) = 3

Ali obstaja rešitev za to težavo? Ali je to edina možna rešitev?

Odgovori

Najprej se oceni obstoj raztopine diferencialne enačbe in da izpolnjuje tudi začetni pogoj. 

V tem primeru f (x, y) = - y Pogoj obstoja je potrebno vedeti, ali  f (x, y) V ravninski regiji je neprekinjen Xy vsebuje koordinatno točko x = 1, y = 3.

Ampak f (x, y) = -y Je povezana funkcija, ki je neprekinjeno v domeni realnih številk in obstaja v celotnem obsegu realnih številk.

Zato je sklenjeno, da je f (x, y) v r neprekinjen², Torej teorem zagotavlja obstoj vsaj ene rešitve.

Če to veste, je čas, da ocenimo, ali je rešitev edinstvena ali nasprotno, več kot ena. Za to je treba izračunati delni derivat F Glede spremenljivke in:

∂f/∂y = ∂ (-y)/∂y = -1

Tako G (x, y) = -1 ki je stalna funkcija, ki je definirana tudi za vse r² In tam je tudi neprekinjeno. Iz tega sledi, da teorem obstoja in edinstvenosti zagotavlja, da ima ta problem začetne vrednosti edinstveno rešitev, čeprav nam ne pove, kaj je.

Vam lahko služi: konveksni poligon: definicija, elementi, lastnosti, primeri

- Primer 2

Upoštevajte naslednjo navadno diferencialno enačbo najprej z začetnim pogojem:

in '(x) = 2√y; in (0) = 0.

Ali obstaja rešitev in (x) za to težavo? Če je tako, ugotovite, ali obstaja eden ali več kot eden.

Odgovor

Upoštevamo funkcijo f (x, y) = 2√y. Funkcija F je opredeljen samo za y≥0, No, vemo, da negativni številki nima pravega korena. Poleg tega f (x, y) Je neprekinjeno v zgornjem semiplanu R²  vključno z osi x, torej Zagotavlja za obstoj in edinstvenost Vsaj ena rešitev v tej regiji.

Zdaj je začetni pogoj x = 0, y = 0 na robu regije raztopine. Nato vzamemo delni derivat F (x, y) glede na Y:

∂f/∂y = 1/√Y

V tem primeru funkcija ni definirana za y = 0, natančno tam, kjer je začetni pogoj.

Kaj nam pove teorem? Pove nam, da čeprav vemo, da obstaja vsaj ena rešitev zgornja semiplana osi x, vključno z osi x, ker stanje edinstvenosti ni izpolnjeno, ni zagotovila, da obstaja ena sama rešitev.

To pomeni, da lahko v območju kontinuitete F (x, y) obstaja ena ali več ene rešitve. In kot vedno nam teorem ne pove, kaj bi lahko bilo.

Rešene vaje

- Vaja 1

Rešite problem Cauchyja iz primera 1:

in '(x) = - y; z in (1) = 3. 

Poiščite funkcijo y (x), ki izpolnjuje diferencialno enačbo in začetni pogoj.

Rešitev

V primeru 1 je bilo ugotovljeno, da ima ta problem rešitev in je tudi edinstven. Za iskanje rešitve je prva stvar, ki jo je treba opaziti, da gre za prvo -stopinjsko diferencialno enačbo ločljivih spremenljivk, ki je napisana na naslednji način:

Vam lahko služi: koeficient variacije: za kaj je, izračun, primeri, vaje

dy /dx = - in → dy = -y dx

Razdelimo se med in v obeh članih, da ločimo spremenljivke, ki jih imamo:

dy/y = - dx

Uporablja se nedoločen integral v obeh članih:

∫ (1/y) dy = - ∫dx

Reševanje nedoločenih integralov je:

ln (y) = -x + c

Kadar je C konstanta integracije, ki jo določa začetni pogoj:

ln (3) = -1 + c, torej C = 1 + ln (3)

Zamenjava vrednosti C in reorganizacije je:

ln (y) - ln (3) = -x + 1

Uporaba naslednje lastnosti logaritmov:

Razlika v logaritmih je količni logaritem

Prejšnji izraz je mogoče napisati tako:

ln (y/3) = 1 - x

Eksponentna funkcija se uporablja z obema članoma za pridobitev:

Y / 3 = e^{(1 - x)}

Ki je enakovredno:

 y = 3e e^-x

To je edinstvena rešitev enačbe in '= -y z y (1) = 3. Graf te rešitve je prikazan na sliki 1.

- Vaja 2

Poiščite dve rešitvi problema, sprožene v primeru 2:

in '(x) = 2√ (y); in (0) = 0.

Rešitev

Je tudi enačba ločenih spremenljivk, ki je napisana različno:

Dy / √ (y) = 2 dx

Jemanje nedoločenega integrala v obeh članih ostaja:

2 √ (y) = 2 x + c

Kot je znano y≥0 V regiji raztopine imamo:

y = (x + c)² 

Ker pa je treba izpolnjevati začetni pogoj x = 0, y = 0, potem je konstanta C enaka nič in naslednja rešitev ostaja:

in (x) = x².

Toda ta rešitev ni edinstvena, funkcija y (x) = 0 je tudi rešitev, ki je bila sprožena. Teorem o obstoju in edinstvenosti, ki se uporablja za to težavo v primeru 2, je že napovedal, da lahko obstaja več kot ena rešitev.

Reference

1. Coddington, Earl A.; Levinson, Norman (1955), Teorija navadnih diferencialnih enačb, New York: McGraw-Hill.
2. Enciklopedija matematike. Cauchy-Lipschitz izrek. Obnovljeno od: enciklopediaofmath.org
3. Lindelöf, Južni L'A Uporaba Methode des A približkov Naslednosti Aux Équations Différentielles Ordinaires du Premier Ordre; Compttes Rendus Hebdomadaires des Séance de l'Anc acadequie des Sciences. Vol. 116, 1894, str. 454-457. Okrevano od: Gallic.Bnf.fr.
4. Wikipedija. Picardovo metodo zaporednih pristopov. Okrevano od: je.Wikipedija.com
5. Wikipedija. Picard-lindelöf izrek. Okrevano od: je.Wikipedija.com.
6. Zill, d.1986. Osnovne diferencialne enačbe z aplikacijami.Dvorana Prentice.