Opredelitev hiperbolične paraboloide, lastnosti in primeri

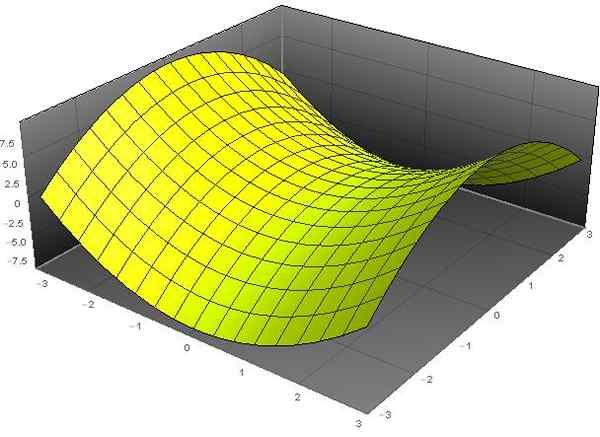
A hiperbolični paraboloid To je površina, katere splošna enačba v kartezijanskih koordinatah (x, y, z) izpolnjuje naslednjo enačbo:

(za)² - (in/b)² - Z = 0.

"Paraboloidna" poimenovanje izhaja iz dejstva, da je spremenljivka Z odvisna od kvadratov spremenljivk x in y. Medtem ko je pridevnik "hiperboličen" posledica dejstva, da ima enačba hiperbole fiksne vrednosti z. Oblika te površine je podobna obliki konjskega jahalnega stola.

Slika 1. Hiperbolični paraboloid z = x² - in². Vir: f. Zapata skozi Wolfram Mathematica.

[TOC]

Opis hiperboličnega paraboloida

Za razumevanje narave hiperboličnega paraboloida bo narejena naslednja analiza:

1.- Poseben primer bo vzet a = 1, b = 1, to pomeni, da kartezijanska enačba paraboloida ostane kot z = x² - in².

2.- Veljajo za vzporedne ravnine z zx ravnino, to je y = ctte.

3.- Z y = ctte je z = x² - C, ki predstavlja prispodobe z vejami navzgor in vrhovnimi.

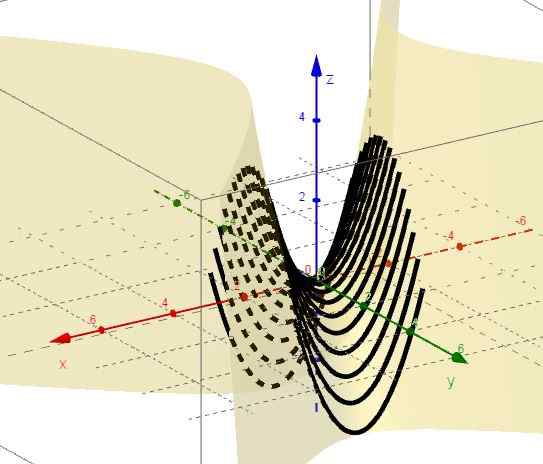Slika 2. Družina krivulj z = x² - C. Vir: f. Zapata skozi Geogebro.

4.- Z x = ctte je z = c - y², ki predstavlja prispodobe z vejami navzdol in vrhom nad ravnino xy.

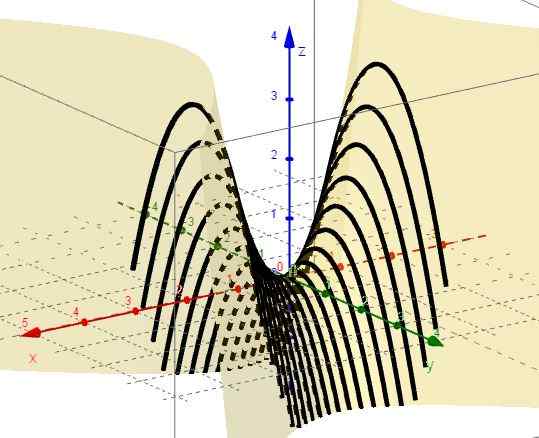Slika 3. Družina krivulj z = c - in². Vir: f. Zapata skozi Geogebro.

5.- Z z = ctte je c = x² - in², ki predstavljajo hiperbole v ravninah vzporedni z ravnino xy. Ko je C = 0, obstajata dve vrstici (A +45 ° in -45 ° glede na osi X), ki sta prestrežena pri izvoru na ravnini XY.

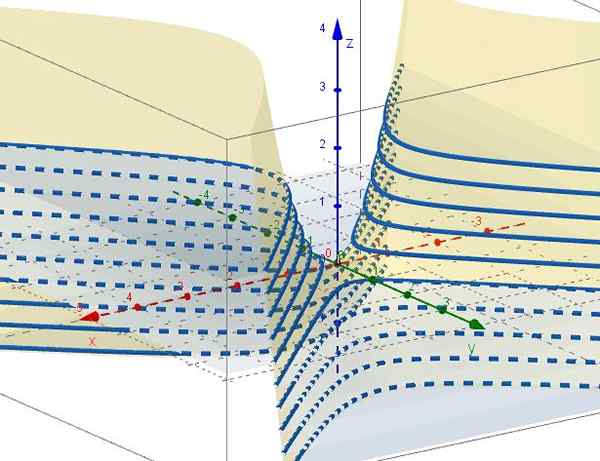Slika 4. Družina krivulj x² - in² = C. Vir: f. Zapata skozi geogebra ..

Lastnosti hiperboličnega paraboloida

1.- Štiri različne točke v tridimenzionalnem prostoru definirajo enega in samo hiperboličnega paraboloida.

Lahko vam služi: omejitve lastnosti (s primeri)

2.- Hiperbolični paraboloid je a dvojno regulirano površino. To pomeni, da kljub temu, da je ukrivljena površina, za vsako točko hiperboličnega paraboloida dve različni črti popolnoma prehajata na hiperbolični paraboloid. Druga površina, ki ni ravnina in je dvojno urejena, je Revolucija hiperboloid.

Prav druga lastnost hiperboličnega paraboloida je omogočila široko uporabo njega v arhitekturi, saj je površina mogoče ustvariti iz žarkov ali ravnih strun.

Druga lastnost hiperboličnega paraboloida omogoča alternativno opredelitev le -te: To je površina, ki jo lahko ustvari ravno mobilna črta, vzporedno s fiksno ravnino, in razreže dve fiksni liniji, ki služita kot vodnik. Naslednja slika pojasnjuje to nadomestno opredelitev hiperboličnega paraboloida:

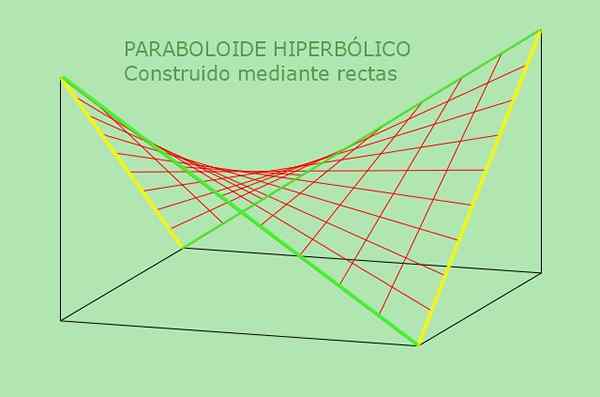Slika 5. Hiperbolični paraboloid je dvojno regulirana površina. Vir: f. Zapata.

Rešeni primeri

- Primer 1

Dokažite, da enačba: Z = xy, ustreza hiperboličnemu paraboloidu.

Rešitev

Preobrazba bo uporabljena v spremenljivkah x in y, ki ustrezajo vrtenju kartezijanskih osi glede na osi z +45. Stare koordinate X in Y se v skladu z naslednjimi odnosi spremenijo v novi X 'E in':

x = x ' - y'

y = x ' + in'

Medtem ko koordinata Z ostaja enaka, to je z = z '.

Z zamenjavo v enačbi z = x in imamo:

z '= (x' - y ') (x' + y ')

Pri uporabi opaznega izdelka razlike za vsoto, ki je enak razliki kvadratov, je:

Z '= x'² - in²

ki jasno ustreza definiciji, ki je bila prvotno dana hiperboličnega paraboloida.

Prestrezanje ravnin vzporedno z osi xy s hiperboličnim paraboloidom z = x in določite enakostranične hiperbole, ki imajo asimptote ravnine x = 0 e y = 0.

Vam lahko služi: Miletus tak teorem

- Primer 2

Določite parametre do in b hiperboličnega paraboloida, ki poteka skozi točke A (0, 0, 0); B (1, 1, 5/9); C (-2, 1, 32/9) in D (2, -1, 32/9).

Rešitev

Po njegovih lastnostih štiri točke v tridimenzionalnem prostoru določajo en sam hiperbolični paraboloid. Splošna enačba je:

Z = (x/a)² - (in/b)²

Nadomestimo dane vrednosti:

Za točko A imate 0 = (0/a)² - (0/b)², enačba, ki je izpolnjena ne glede na vrednosti parametrov A in B.

Zamenjava točke B dobimo:

5/9 = 1/a² - 1 b²

Medtem ko za točko C ostaja:

32/9 = 4/a² - 1 b²

Končno za točko D dobimo:

32/9 = 4/a² - 1 b²

Ki je enak prejšnji enačbi. Skratka, sistem enačb je treba rešiti:

5/9 = 1/a² - 1 b²

32/9 = 4/a² - 1 b²

Odštevanje druge enačbe prvega je dobimo:

27/9 = 3/a² kar to pomeni² = 1.

Podobno se odšteje druga enačba štirikotnika prvega in pridobi:

(32-20)/9 = 4/a² - 4/a² -1 b² + 4/b²

To je poenostavljeno kot:

12/9 = 3/b² ⇒ b² = 9/4.

Skratka, hiperbolični paraboloid, ki poteka skozi točke A, B, C in D, ima kartezijansko enačbo, ki jo daje:

Z = x² - (4/9) in²

- Primer 3

Glede na lastnosti hiperboličnega paraboloida, dve črti, ki sta v njej popolnoma vsebovani za vsako točko. Za primer z = x^2 - y^2 Poiščite enačbo obeh vrstic, ki prehajata skozi točko P (0, 1, -1), ki očitno pripada hiperboličnemu paraboloidu, tako da vse točke teh vrstic pripadajo tudi enako.

Rešitev

Z izjemnim izdelkom razlike v kvadratih lahko enačbo hiperboličnega paraboloida zapišemo na naslednji način:

Vam lahko služi: štirikolesni: elementi, lastnosti, klasifikacija, primeri

(x + y) (x - y) = c z (1/c)

Kjer je C konstanta nič.

Enačba x + y = c z in enačba x - y = 1/c ustrezata dvema ravninama z običajnimi vektorji n= y m=. Vektorski izdelek m x n = Smer linijskega presečišča obeh ravnin nam daje. Potem ima ena od vrstic, ki prehaja skozi točko P in pripada hiperboličnemu paraboloidu, parametrična enačba:

= + t

Za določitev c nadomestimo točko P v enačbi x + y = c z, pridobimo:

C = -1

Podobno, vendar glede na enačbe (x - y = k z) in (x + y = 1/k) imate parametrično enačbo vrstice:

= + s s k = 1.

Skratka, dve vrstici:

= + t y = + s

So popolnoma vsebovani v hiperboličnem paraboloidu z = x² - in² skozi točko (0, 1, -1).

Kot ček predpostavimo t = 1 Kaj nam daje točko (1,2, -3) v prvi vrstici. Preveriti morate, ali je tudi na paraboloidu z = x² - in²:

-3 = 1² - 2² = 1 - 4 = -3

Ki potrjuje, da dejansko pripada površini hiperboličnega paraboloida.

Hiperbolični paraboloid v arhitekturi

Slika 6. Oceanographic of Valencia (Španija).Vir: Wikimedia Commons.

Hiperbolični paraboloid so v arhitekturi uporabili veliki avantgardni arhitekti, med katerimi so imena španskega arhitekta Antonija Gauda (1852-1926) in še posebej španska tudi španska félix Candela (1910-1997) zelo posebej posebej posebej.

Spodaj je nekaj del, ki temeljijo na hiperboličnem paraboloidu:

-Kapela mesta Cuernavaca (Mehika) Dela arhitekta Félixa Candela.

-Oceanographic v Valenciji (Španija), tudi Félix Candela.

Reference

1. Enciklopedija matematike. Vladala površina. Obnovljeno od: enciklopediaofmath.org
2. Llera Rubén. Hiperbolični paraboloid. Okrevano od: Rubenllera.WordPress.com
3. Weisstein, Eric W. "Hiperbolični paraboloid.”Iz spletnega vira MathWorld-A Wolfram. Okreval od: Mathworld.Wolfram.com
4. Wikipedija. Paraboloid. Pridobljeno iz: v.Wikipedija.com
5. Wikipedija. Paraboloid. Okrevano od: je.Wikipedija.com
6. Wikipedija. Vladala površina. Pridobljeno iz: v.Wikipedija.com