Lamyjev teorem
- 2666
- 840
- Lee Farrell

Lamyjev teorem ugotovi, da ko je togo telo v ravnovesju in ob delovanju treh sil (sil, ki so v isti ravnini), se njihove delovne linije strinjajo na isti točki.
Teorem je sklepal francoski fizik in verski. Široko se uporablja za iskanje vrednosti kota, akcijske linije sile ali za oblikovanje trikotnika sil.
Pojasnilo
Teorem določa, da morajo biti sile za izpolnjevanje stanja ravnotežja koplanare; to pomeni, da je vsota sil, ki se izvajajo na točki.
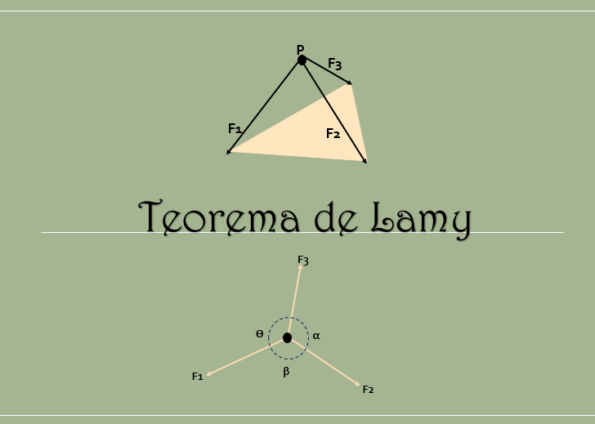
Poleg tega se, kot je razvidno iz naslednje slike, izpolnjeno, da se s podaljšanjem linij teh treh sil strinjajo na isti točki.
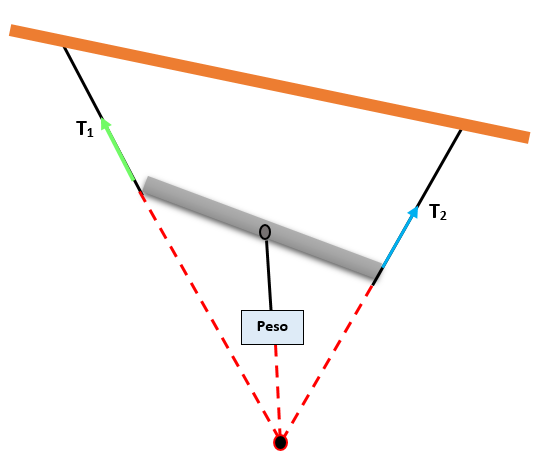
Če torej tri sile, ki so v isti ravnini in sočasni, bo velikost vsake sile sorazmerna z naročjem nasprotnega kota, ki jo tvorita druga dve sili.
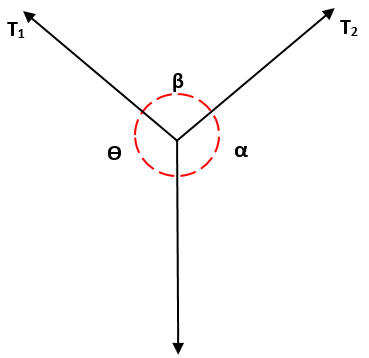
To mora T1, ki se začne od dojke α, je enak razmerja T2 / β, kar je posledično enako razmerju T3 / ɵ, to je:
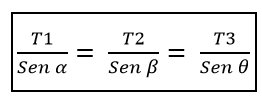
Od tam sledi, da morajo biti moduli teh treh sil enaki, če so koti, ki tvorijo vsak par sil, enaki 120 °.
Obstaja možnost, da je eden od zornih kotov obljuden (merite med 900 in 1800). V tem primeru bo dojka tega kota enaka krosu dodatnega kota (v svojem paru meri 1800).
Vam lahko služi: zakoni eksponentovVaja rešena
Obstaja sistem, ki ga tvorita dva bloka J in K, ki visijo na več strunah, ki tvorijo kote glede na vodoravno, kot je prikazano na sliki. Sistem je v ravnovesju in blok J tehta 240 n. Določite težo bloka k.
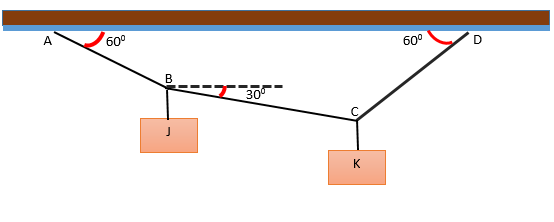
Rešitev
Po načelu delovanja in reakcije bodo napetosti, ki se izvajajo v blokih 1 in 2.
Zdaj je za vsak blok zgrajen prosti karoserijski diagram in tako določite kote, ki tvorijo sistem.
Znano je, da ima vrv, ki gre na A do B, kot 300 , tako da je kot, ki dopolnjuje, enak 600 . Tako dosežete 900.
Po drugi strani, kjer se nahaja točka A, je kot 600 Glede na vodoravno; Kot med navpično in tDo Bo = 1800 - 600 - 900 = 300.
Tako se pridobi, da je kot med AB in BC = (300 + 900 + 300) in (600 + 900 + 60) = 1500 in 2100. Ko se pridruži, je preverjeno, da je skupni kot 3600.
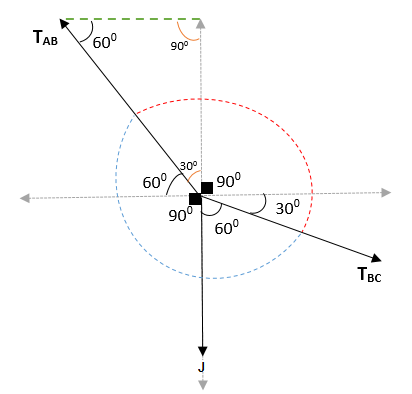
Če uporabite Lamyjev teorem, morate:
TPr/ greh 1500 = PDo/ greh 1500
TPr = PDo
TPr = 240n.
V točki C, kjer je blok, je kot med vodoravno in vrvjo BC 30 je 300, Torej je dopolnilni kot enak 600.
Po drugi strani je kot 600 na CD točki; Kot med navpično in tC Bo = 1800 - 900 - 600 = 300.
Vam lahko služi: Coplanares Točke: enačba, primer in rešene vajeTako se pridobi, da je kot v bloku k = (300 + 600)
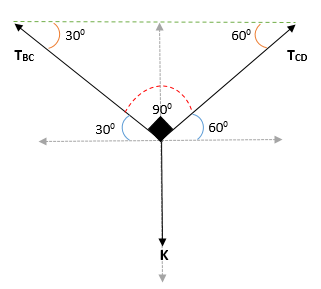
Uporaba Lamyjevega teorema v točki C:
TPr/ greh 1500 = B / Sin 900
Q = tBC * Sen 900 / greh 1500
Q = 240 N * 1/0.5
Q = 480 n.
Reference
- Ferdinand P. Pivo, npr. R. (2013). Mehanika za inženirje, statična. McGraw-Hill Interamerican.
- Francisco Español, J. C. (2015). Rešeni problemi linearne algebre. Paraninfo Editions, s.Do.
- Graham, J. (2005). Moč in gibanje. Houchton Mifflin Harcourt.
- Harpe, str. d. (2000). Teme v teoriji geometrijske skupine. University of Chicago Press.
- Str. A tpler y, g. M. (2005). Fizika za znanost in tehnologijo. Zvezek I. Barcelona: Vrnite te.Do.

