Teleskopsko poletje, kako je rešena in rešena vaje

The povzetek Teleskopska Je veja operacij s številčnimi serijami. Nagovori povzetke elementov od začetne vrednosti do „n“ izrazov, katerih argument je posledica katerega koli od naslednjih vzorcev:

(F_x - F_x+1); F_x+1  - F_x)

Kjer je njen povzetek izraz opredeljen na naslednji način: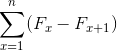

Tudi:

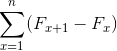
Vir: Pixabay.com

Predstavljajo vsoto elementov, ki so pri razvoju podvrženi odpovedi nasprotnih izrazov. Povzroči naslednjo enakost za teleskopske povzetke:

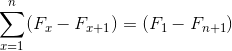
Njeno ime izhaja iz odnosa z videzom klasičnega teleskopa, ki bi ga bilo mogoče zložiti in namestiti, kar bistveno spremeni njegovo dimenzijo. Podobno lahko teleskopska povzetka, ki so po njihovi naravi neskončna, povzamemo v poenostavljenem izrazu:

F₁ - F_N+1

[TOC]

Demonstracija

Pri razvijanju vsote izrazov je odprava dejavnikov povsem očitna. Kjer se bodo za vsak primer pojavili nasprotni elementi v naslednji iteraciji.

Prvi primer bo vzet kot primer (f_x - F_x+1), ker postopek deluje homologno (f_x+1-F_x).

Razvoj prvih 3 vrednosti 1, 2, 3 Opazimo težnjo poenostavitve

X₁     (F₁ - F₁₊₁) = F₁ - F₂

X₂     (F₂ - F₂₊₁) = F₂ - F₃

X₃     (F₃ - F₃₊₁) = F₃ - F₄

Kjer z izražanjem vsote opisanih elementov:

X₁ + X₂ + X₃ = F₁ - F₂ + F₂ - F₃ + F₃ - F₄

Opazimo, da so izrazi f₂ in f₃ Opisani so s svojimi nasprotji, zaradi česar je njihova poenostavitev neizogibna. Na enak način je opaziti, da so izrazi f₁ in f₄ ostati.

Če je bila vsota narejena od x = 1 do x = 3, to pomeni, da element F₄ ustreza generičnemu izrazu F_N+1.

Tako dokazuje enakost:

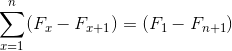
Kako je rešeno?

Namen teleskopskih povzetkov je olajšati delo, tako da ni treba razviti neskončne količine izrazov ali poenostaviti nekaj predolge verige.

Vam lahko služi: Trachtenberg metoda: kaj je, primeri

Za reševanje bo potrebno le za oceno izrazov F₁ in f_N+1. Te preproste nadomestitve predstavljajo končni rezultat vsote.

Celovitost izrazov ne bo izražena, saj postane potrebna za demonstracijo rezultata, ne pa tudi za običajni postopek izračuna.

Pomembno je, da opazite konvergenco numerične serije. Včasih argument vsote ne bo izražen na teleskopski način. V teh primerih je izvajanje alternativnih metod faktorizacije zelo pogosto.

Karakteristična faktorizacijska metoda v teleskopskih povzetkih je preprosta ulomka. To se zgodi, ko se originalni del razpade v vsoto več ulomkov, kjer je mogoče opaziti teleskopski vzorec (F_x - F_x+1) ali (f_x+1  - F_x).

Razgradnjo v preprostih ulomkih

Za preverjanje konvergence številčnih serij je zelo pogosto preoblikovati racionalne izraze z metodo preprostih frakcij. Cilj je modelirati argument do oblike teleskopskega seštevanja.

Na primer, naslednja enakost predstavlja razgradnjo v preprostih frakcijah:

Pri razvoju numeričnih serij in uporabi ustreznih lastnosti je izraz, ki ga izraz traja na naslednji način:

Kjer je mogoče videti teleskopsko obliko (f_x - F_x+1).

Postopek je precej intuitiven in je sestavljen iz iskanja vrednosti števca, ki brez prekinitve enakosti omogočajo ločevanje izdelkov, ki so v imenovalcu. Enačbe, ki nastanejo pri določanju teh vrednosti.

Ta postopek opazimo korak za korakom pri razvoju vaje 2.

Vam lahko služi: 6 zabavnih matematičnih ugank za otroke

Zgodovina

Precej negotovo je, da lahko opredelimo zgodovinski trenutek, v katerem so bile predstavljene teleskopske povzetke. Vendar se njegovo izvajanje začne vidno v sedemnajstem stoletju, v numeričnih serijah, ki sta jih izvedla Leibniz in Huygens.

Oba matematika, ko raziskujeta povzetke trikotnih številk, začneta opažati trende v konvergenci nekaterih serij zaporednih elementov. Še bolj zanimiv pa je začetek modeliranja teh izrazov, v elementih, ki se ne zgodijo nujno.

Pravzaprav se izraz, ki se je prej uporabljal za sklicevanje na preproste frakcije:

Predstavil ga je Huygens in takoj poklical Leibnizovo pozornost. Kdo bi sčasoma lahko opazoval konvergenco do vrednosti 2. Ne da bi to vedel, je implementiral teleskopsko povzetek.

Vaje

Vaja 1

Določite, kateri izraz se konvergira naslednja vsota:

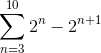
Ko se vsota razvije ročno, opazimo naslednji vzorec:

(2³ - 2⁴) + (2⁴ - 2⁵) + (2⁵ - 2⁶)… (2¹⁰ - 2^enajst)

Kjer so dejavniki od 2⁴ do 2¹⁰ Predstavljajo pozitivne in negativne dele, kar kaže na njihovo odpoved. Potem bodo edini dejavniki, ki ne bodo poenostavljeni, prvi "2³"In zadnji" 2^enajst".

Na ta način se pri izvajanju teleskopskih meril povzetka dobi:

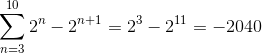
Vaja 2

Preoblikujte argument v teleskopsko vsoto tipa in določite konvergenco serije:

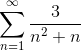
Kot je navedeno v izjavi, bo prva stvar razgradnja v preprostih ulomkih, da bi ponovno premislili argument in ga izrazili v teleskopski obliki.

2 ulomka, katerih imenovalca sta "N" in "N+1", je treba najti, kjer mora spodnja metoda doseči vrednosti štetja, ki ustrezajo enakosti.

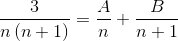
Vrednosti A in B so definirane. Izdelana je prva vsota frakcij.

Vam lahko služi: 60 delitev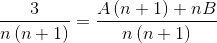

Nato so poenostavljeni imenovalci in vzpostavi se linearna enačba.

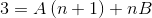
V naslednjem koraku deluje izraz desne, dokler vzorec, primerljiv s "3" na levi strani.

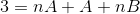
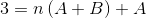
Za določitev enačb, ki jih je treba uporabiti, je treba primerjati rezultate obeh strani enakosti. To pomeni, da na levi strani ne opazimo nobenih spremenljivih n vrednosti, na ta način bo A +B moralo biti enak nič.

A + b = 0; A = -b

Po drugi strani bo morala biti konstantna vrednost enaka konstantni vrednosti 3.

A = 3

Zato.

A = 3 in b = -3

Že definirane vrednosti števca za preproste frakcije, vsota se premisli.

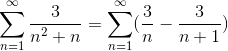
Kjer je bila že dosežena splošna oblika teleskopskega povzetka. Razvita je teleskopska serija.

Kjer se bo z delitvijo z zelo velikim številom rezultat približal vedno več, in opazovanje konvergence serije na vrednost 3.

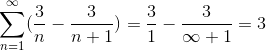
Te vrste serij ni bilo mogoče z drugimi besedami rešiti, zaradi neskončne količine iteracij, ki opredeljujejo težavo. Vendar ta metoda skupaj z mnogimi drugimi uokvirja vejo preučevanja numeričnih serij, katere cilj je določiti vrednosti konvergence ali določiti razhajanje teh serij.

Reference

1. Neskončni lekcije za izračun. Manuel Franco, Manuel Franco Nicolás, Francisco Martínez González, Roque Molina Legaz. Uredi, 1994.
2. Celovit izračun: nasledstvo in niz funkcij. Antonio Rivera Figueroa. Uredniška skupina Patria, 21. oktobra. 2014.
3. Tečaj v računu in resnični analizi. Sudhir r. Ghorpade, Balmohan V. Limaye. Springer Science & Business Media, 5. junij. 2006.
4. Neskončna serija. TOMLINSON FORT. Clarendon Press, 1930.
5. Elementi teorije neskončnih procesij. Lloyd Leroy Smail. McGraw-Hill Book Company, Incorpan, 1923.