Matematika

Vsota zgodovine Riemanna, formul in lastnosti, vaje

Vsota zgodovine Riemanna, formul in lastnosti, vaje

The Riemann vsota To je ime, ki prejme približni izračun določenega integrala s pomočjo diskretne vsote s končnim številom izrazov. Skupna aplikacija je pristop območja funkcij v grafiki.

Nemški matematik Georg Friedrich Bernhard Riemann (1826-1866) je prvič ponudil strogo opredelitev integracije funkcije v določenem intervalu. Napovedal je v članku, objavljenem leta 1854. 

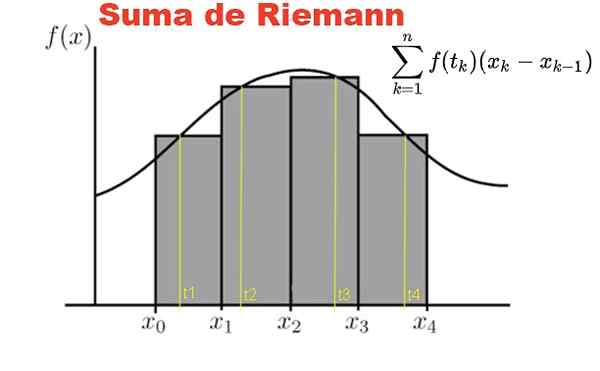
Slika 1. Riemannova vsota je opredeljena na funkciji F in particiji v intervalu [x0, x1]. Vir: Fanny Zapata.

Riemannova vsota je opredeljena na funkciji y = f (x), pri čemer X pripada zaprtemu intervalu [a, b]. V tem intervalu je narejena particija p n elementov:

P = x0= a, x1, x2,…, Xn= B

To pomeni, da je interval razdeljen na naslednji način:

 Tukaj tk je med xK-1 in xk:

xK-1 ≤ tk ≤ xk

Slika 1 prikazuje vsoto Riemanna funkcije F v intervalu [x0, x4] Na delitvi štirih podtemej, sivih pravokotnikov.

Vsota predstavlja skupno površino pravokotnikov in rezultat te vsote je številčno pristopi k območju pod krivuljo F, med abscisami x = x0 y x = x4.

Seveda se pristop k območju pod krivuljo močno izboljša do te mere, da je številka n predelnih del je večje.  Na ta način se vsota konvergira na območje pod krivuljo, ko je številka n predelne stene se nagibajo k neskončnosti.

[TOC]

Formule in lastnosti

Riemannova vsota F (x) Funkcija na particiji:

Vam lahko služi: Rhomboid: značilnosti, kako odnesti obod in območje

P = x0= a, x1, x2,…, Xn= B

Definiran v intervalu [a, b], daje ga:

S (p, f) = ∑K = 1n f (tk) (xk - xK-1) 

Kjer tk Je vrednost v intervalu [xk, xK-1]. V vsoti Riemanna se običajno uporabljajo redni intervali širine Δx = (b - a)/n, kjer sta A in B najmanjše in največje vrednosti abscisa, n pa število pododdelkov.

V tem primeru Riemannova prava vsota je:

Sd (f, n) = [f (a+Δx)+f (a+2Δx)+…+f (a+(n-1) Δx)+f (b)]*Δx

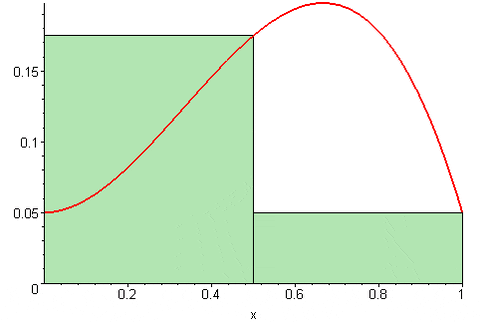Slika 2. Riemannova prava vsota. Vir: Wikimedia Commons. 09Glasgow09 [CC BY-SA (https: // creativeCommons.Org/licence/by-sa/3.0)].

Medtem ko Riemannova leva vsota Je izražen kot:

Da (f, n) = [f (a)+f (a+Δx)+…+f (a+(n-1) Δx)]*Δx

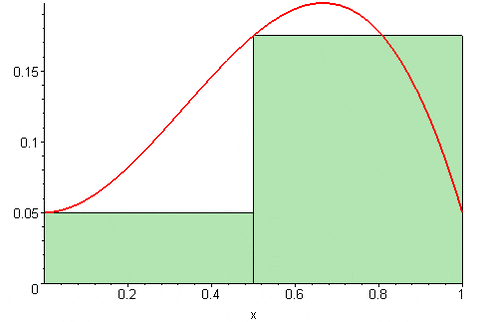Slika 3. Vsota Riemanna. Vir: Wikimedia Commons. 09Glasgow09 [CC BY-SA (https: // creativeCommons.Org/licence/by-sa/3.0)]

Končno Riemann Central Sum je:

Sc (f, n) = [f (a+Δx/2)+f (a+3Δx/2)+…+f (b- Δx/2)]*Δx

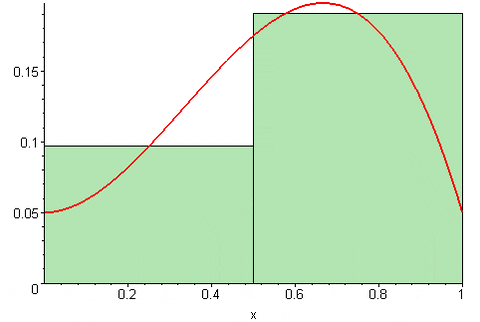Slika 4. Vmesna vsota Riemanna. Vir: Wikimedia Commons. 09Glasgow09 [CC BY-SA (https: // creativeCommons.Org/licence/by-sa/3.0)]

Odvisno od tega, kje se nahaja točka Tk V intervalu [xk, xK-1] Riemannova vsota lahko precenjuje ali podcenjuje natančno vrednost območja pod krivuljo funkcije y = f (x) (x). To pomeni, da se pravokotniki lahko odlikujejo od krivulje ali so nekoliko pod to.

Območje pod krivuljo

Glavna lastnost vsote Riemanna in katere postane njegov pomen, je, da če se število pododdelkov nagiba k neskončnosti, se rezultat vsote zbliža v definirani integral funkcije:

Prejšnji izraz ustreza definiciji Riemannovega integrala in velja, da je funkcija F neprekinjena in mehka. Za bolj določene funkcije obstajajo druge opredelitve integrala (integral de Stieldjes in Integral de Lebesgue).

Lahko vam služi: standardna ocena napaka: kako se izračuna, primeri, vaje

Rešene vaje

- Vaja 1

Izračunajte vrednost integra, definiranega med A = -2 do B = +2 funkcije:

f (x) = x2

Izkoristite vsoto Riemanna. Če želite to narediti, poiščite vsoto za redne particije intervala [a, b] in nato vzemite matematično mejo za primer, da se število particij shrani v neskončnost. 

Rešitev

To so koraki, ki jih je treba slediti:

-Prvič, interval predenja je opredeljen kot: 

Δx = (b - a)/n. 

-Potem je vsota Riemanna na desni strani, ki ustreza funkciji f (x), taka:

-Zdaj jih nadomestimo a = -2 in b =+2, tako da je interval ali korak Δx = 4/n. To pomeni, da je vsota Riemanna za funkcijo f (x) = x2 je:

-Potem je razvit kvadratni binomial: 

[-2 +(4i/n)]2 = 4 - (16 i /n) + (4 /n)2 Yo2

-In potem ga skrbno zamenjamo v znesku:

-Naslednji korak je, da ločite povzetke in odstranite konstantne količine kot skupni dejavnik vsake vsote. Je treba upoštevati, da je indeks jaz, torej številke in izrazi n Se štejejo za stalne:

-Vsak vsota se oceni, saj za vsakega od njih obstajajo ustrezni izrazi. Na primer, prvi od povzetkov da n:

Drugi je:

 In tretja je:

 -Če nadomestimo rezultate povzetkov v vsoti Riemanna, je končno pridobljeno:

S (f, n) = 16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n2

-Končno morate izračunati integral::

= limN➝∞ [16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n2] =

= 16 -(64/2) + (64/3) = 16/3 = 5.333

Bralec lahko preveri, ali je to natančen rezultat, ki ga je mogoče dobiti z reševanjem nedoločenega integrala in ocenjevanjem meja integracije s pravilom Barrow.

Vam lahko služi: kako pretvoriti iz km/h a m/s? Rešene vaje

- Vaja 2

Določite približno območje pod funkcijo: 

f (x) = (1/√ (2π) e(-x2/2)

Med x = -1 in x =+1, z uporabo osrednje vsote Riemanna z 10 particijami. Primerjajte z natančnim rezultatom in ocenite odstotno razliko.

Rešitev

Korak ali povečanje med dvema zaporednima diskretnima vrednostima je:

Δx = (1 - (-1)/10 = 0,2

Tako da je particija, na kateri so definirani pravokotniki, taka:

P = -1,0; -0,8; -0,6; -0,4; -0,2; 0,0; 0,2; 0,4; 0,6; 0,8; 1.0

Toda kot želite, bo funkcija F (x) ocenjena v srednjih točkah podintralov, torej v naboru:

T = -0,9; -0,7; -0,5; -0,3; -0,1; 0,1; 0,3; 0,5; 0,7; 0,9.

Riemannova vsota (osrednja) je taka:

S = F (-0,9)*0,2 +F (-0,7)*0,2 +F (-0,5)*0,2 +… +f (0,7)*0,2 +f (0,9)*0.2

Ker je funkcija F simetrična, je mogoče zmanjšati vsoto na samo 5 izrazov in rezultat se pomnoži z dvema:

S = 2*0,2*F (0,1)+ F (0,3)+ F (0,5)+ F (0,7)+ F (0,9)

S = 2*0,2*0,397+ 0,381+ 0,352+ 0,312+ 0,266 = 0,683

Funkcija, navedena v tem primeru, ni nič drugega kot dobro znan Gauss Bell (normalizirana, s povprečjem, ki je enaka nič in standardni odklon). Znano je, da je območje pod krivuljo v intervalu [-1,1] za to funkcijo 0,6827.

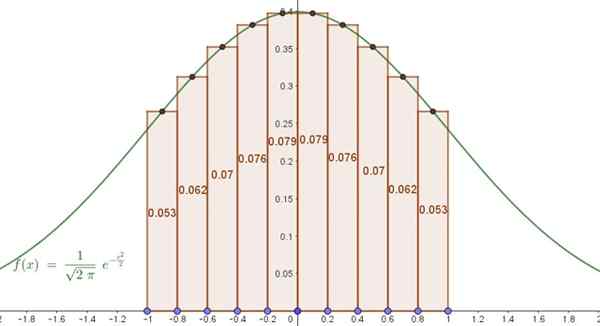Slika 5. Območje pod približnim zvoncem Gauss s pomočjo vsote Riemanna. Vir: f. Zapata.

To pomeni, da približna rešitev s samo 10 izrazi sovpada z natančno rešitvijo do treh decimalk. Odstotna napaka med približnim integralom in natančno je 0,07%.

Reference

  1. Casteleiro, J. M., & Gómez-Alvarez, R. Str. (2002). Celovit izračun (ilustrirano ed.). Madrid: uredništvo ESIC.
  2. Uničen. Zgodovina koncepta integrala. Obnovi se od: skladišče.Uničen.je
  3. UIS. Riemann vsota. Okrevano od: matematika.UIS.Edu.co
  4. Wikipedija. Riemann vsota. Okrevano od: je.Wikipedija.com
  5. Wikipedija. Integracija Riemanna. Okrevano od: je.Wikipedija.com