Vrste, aplikacije, primeri stožčastih odsekov

The Konični odseki So krivulje, ki jih dobimo s prestrezanjem letala s stožcem. Obstaja več načinov za to; Na primer, če se ravnina prenaša pravokotno na osno os stožca, dobimo obod.

Malo nagibanje ravnine glede na osno os stožca dobimo elipse, krivulja, ki je zaprta, če pa jo nagibamo, dobimo še bolj parabolo ali hiperbola, kot je razvidno iz animacije slike 1.

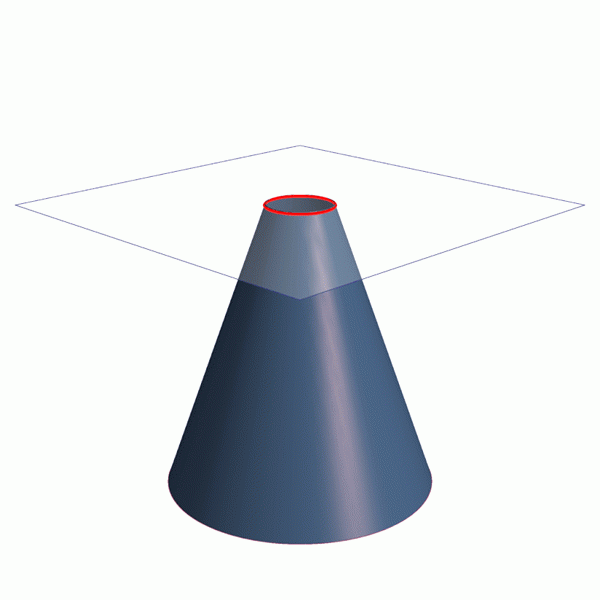Animacija, ki prikazuje, kako pridobiti štiri stožčaste odseke: obod, prispodoba in hiperbola elipse. Vir: Wikimedia Commons. Vrstice / cc0

Konični odseki so del narave in sveta okoli nas. Inženiring, arhitektura in astronomija so pomembne veje znanja, ki uporabljajo konike.

[TOC]

Pogoji za stožčaste odseke

Konični odseki so opredeljeni kot geometrijska mesta, ki izpolnjujejo naslednje pogoje:

Prispodoba

Geometrijsko mesto vseh točk leži v enako oddaljeni ravnini do fiksne točke osredotočenost F in naravnana črta, imenovana, imenovana direktiva.

Elipsa

Ravninska točka pripada elipsi, če se vsota razdalj med to točko in dvema drugim fiksnim točkam imenuje Focos in se nahaja na glavna os elipse ostaja konstantna.

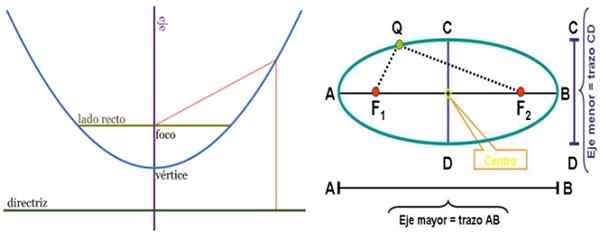Prispodoba na levi in ​​elipsi desno, z ustreznimi elementi. Žarišča so točke s številnimi aplikacijami. Vir: Wikimedia Commons.

Obod

To je geometrijsko mesto vseh točk, ki vzdržujejo enako razdaljo do druge točke, imenovane Centro. Ta razdalja je radio oboda.

Vam lahko služi: evklidska razdalja: koncept, formula, izračun, primer

Hiperbola

Nabor točk v ravnini, tako da je razlika med njeno razdaljo do dveh določenih točk, imenovanih Focos, To je konstantno.

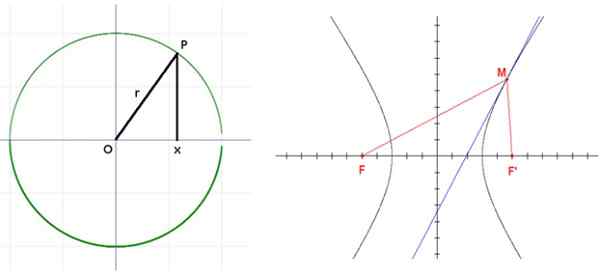Hiperbola z žarišči f in f. Vir: Wikimedia Commons.

Prijave

Poglejmo nekaj aplikacij za stožčaste odseke:

Prispodobe  

-Ko se objekt sproži, ima usmeritev, ki sledi.

-Prispodobe imajo opazne inženirske aplikacije, na primer v suspendiranih mostovih, kabli pohitijo v obliki prispodobe.

-Tudi prispodobe so dobre za izdelavo reflektorjev in teleskopov. To je zahvaljujoč zanimivi lasti: pri postavljanju svetilke v osredotočenost površine paraboličnega prečnega odseka bo svetloba v vzporednih žarkih potovala do osi prispodobe.

-Če se svetleči žarki vzporedno z osi simetrije približajo parabolični površini, jih koncentrira v fokusu, okoliščina, ki se uporablja za izdelavo reflektorskih teleskopov, kot je teleskop Hale de Monte Palomar.

Elipse

-Planeti sončnega sistema se premikajo po eliptičnih usmeritvah, precej blizu oboda v primeru večjih planetov, vključenih zemljišč. Sonce ni v središču, ampak v enem od osvetlitev.

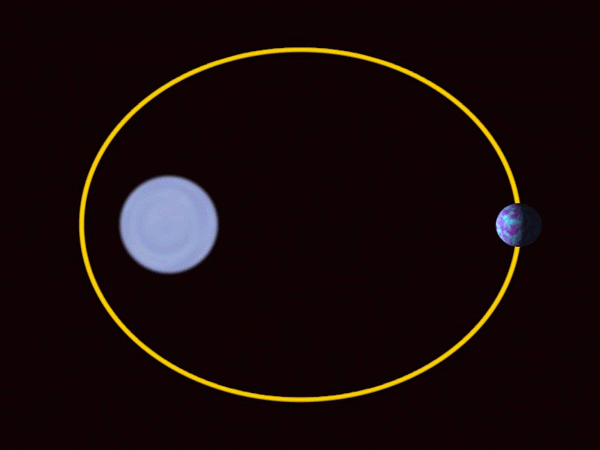Planeti sončnega sistema se premikajo v eliptičnih orbitah s soncem v enem od osvetlitev. Vir: Wikimedia Commons.

-Elipsa se v arhitekturi pogosto uporablja kot dekorativni in oblikovalski element.

-Z namestitvijo reflektorja v eno od osvetlitve elipse se svetloba odraža proti drugemu fokusu. Enako se zgodi z zvokom. Zato v dvorani v obliki Ellipse, ki tiho govorijo, da se nahajajo v enem fokusu.

Lahko vam služi: hepagonska prizma

-Ta ista lastnost ima presenetljivo aplikacijo na področju medicine. Izračuni ledvic lahko uničijo zvok. Ultrazvočni valovi velike intenzivnosti nastajajo v eni od žarišč eliptične kadi, polne vode, pacient pa se nahaja v drugem fokusu. Zvočni valovi vplivajo in razmišljajo v izračunu, s svojo energijo.

Hiperbole

-Nekateri kometi v osončju sledijo hiperboličnim usmeritvam, vedno s soncem v eni od žarišč.

-Hyperbolas Focus so zelo zanimivi tudi za preučevanje pojavov refleksije valov. Na primer, z usmerjanjem svetlobnega žarka v žarišče paraboličnega ogledala se odraža v drugem fokusu, zelo uporabna lastnost za gradbene teleskope, saj se lahko svetloba osredotoči na parabolično ogledalo in se preusmeri na drugo bolj primerno mesto Po oblikovanju.

-Hladilni stolpi jedrskih rastlin imajo silhueto v obliki hiperbole.

-Pred pojavom GPS so hiperbole uporabili v navigaciji za iskanje čolnov. Ladje, ki jih nosijo signale, ki so jih hkrati izdali postaje radia in B, in računalnik je bil odgovoren za registracijo razlik v času prihoda signalov, da bi jih spremenili v razlike v razdaljah razdalj. Na ta način se ladja nahaja v veji hiperbole.

Postopek se ponovi z dvema postajama drugimi radijskimi C in D, ki ladjo postavi v vejo Še ena hiperbola. Dokončni položaj čolna je presečišče obeh hiperbole.

Lahko vam služi: Graščanje funkcije: Kako jo prepoznati, primeri, vaje

Obobov

-Prihod kolesa je spremenil potek zgodovine.

-Krožno gibanje je zelo pogosto, veliko kosov se vrti tako, da ustvarja različne učinke, od mlinov do ventilatorjev.

-Čeprav so usmeritve glavnih planetov eliptične, so krožne usmeritve v mnogih primerih dobri pristopi.

-Circunferences so pogosti elementi v arhitekturi, oblikovanju, inženiringu in gradnji. Seznam krožnih ali diskovnih oblik je neskončen: kovanci, CD -je, ure in še več.

Primeri

Potem sta v ravnini dva konika, krog in elipsa.

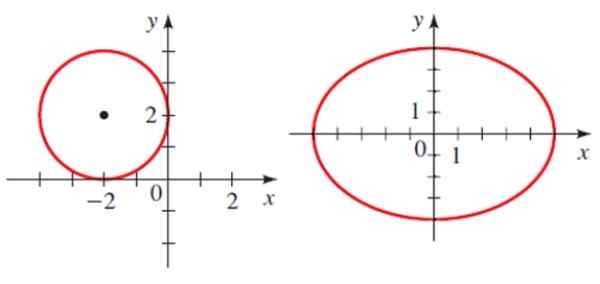Primeri stožčastih odsekov: krog in elipsa. Vir: Stewart, J. Prekalenkulacija.

Vsak ima analitično enačbo:

Obod

(X-h)² + (Y-k)² = R²

Kjer sta H in K koordinata centra in je R radio. Za obod, prikazan na sliki, je enačba:

(x+2)² + (Y-2)² = 4

Elipsa

Elipse enačba, katere središče je koordinatna točka (H, K):

[(X-H)² /do² ]+ [(y-k)² /b² ] = 1

Kjer sta a in b pol -pila elipse. Za prikazano elipso je središče v točki 0,0, največji pol -njun je enak in manjši polži je 4. Zato je njegova enačba:

(x² /25)+ (in² / 16) = 1

Reference

1. Hoffman, J. Izbira vprašanj matematike. Zvezek 2.
2. Jiménez, r. 2008. Algebra. Dvorana Prentice.
3. Stewart, J. 2006. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.
4. Wikipedija. Konični odsek. Okrevano od: je.Wikipedija.org.
5. Zill, d. 1984. Algebra in trigonometrija. McGraw Hill.