Tukey test v tem, kar je, mojster, vaja rešena

The Tukey test To je metoda, ki želi primerjati posamezna povprečna vrednost iz analize variance več vzorcev pod.

Test, ki ga je leta 1949 predstavil John.W. Tukey, omogoča ugotovitev, ali so pridobljeni rezultati bistveno različni ali ne. Znan je tudi kot Tukey pošteno pomemben test razlike (Tukeyjev HSD test za svojo kratico v angleščini).

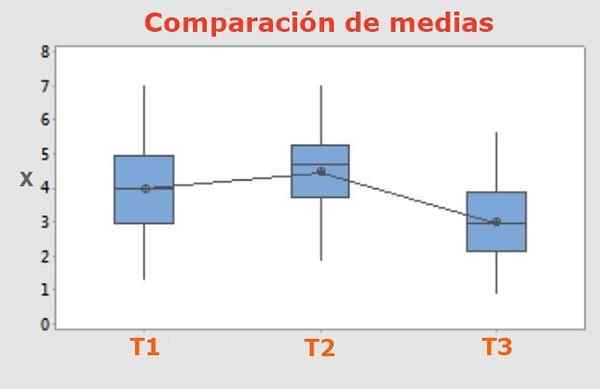
Slika 1. Tukey test omogoča ugotovitev, ali imajo razlike v rezultatu med tremi ali več različnimi tretmaji, ki se uporabljajo za tri ali več skupin enakih značilnosti, pomembne in pošteno različne povprečne vrednosti.

V poskusih, kjer primerja med tremi ali več različnimi zdravljenji, ki se uporabljajo za isto število vzorcev, je treba ugotoviti, ali so rezultati bistveno različni ali ne.

Rečeno je, da je poskus uravnotežen, ko je velikost vseh statističnih vzorcev enaka pri vsakem zdravljenju. Ko je velikost vzorčenja za vsako zdravljenje drugačna, potem obstaja ne uravnotežen eksperiment.

Včasih ni dovolj z analizo variance (ANOVA), da bi vedeli, ali v primerjavi različnih načinov zdravljenja (ali poskusov), uporabljenih za več vzorcev izpolnjuje alternativno hipotezo (HA: "vsaj eno od zdravljenja je drugačno").

Tukey test ni edinstven, obstaja veliko več dokazov za primerjavo vzorčnih sredstev, vendar je to eden najbolj znanih in uporabljenih.

[TOC]

Primerjalna in Tukey tabela

Pri uporabi tega testa se izračuna vrednost W imenovan Tukey primerjalnik katere definicija je naslednja:

W = Q √ (MSE /R)

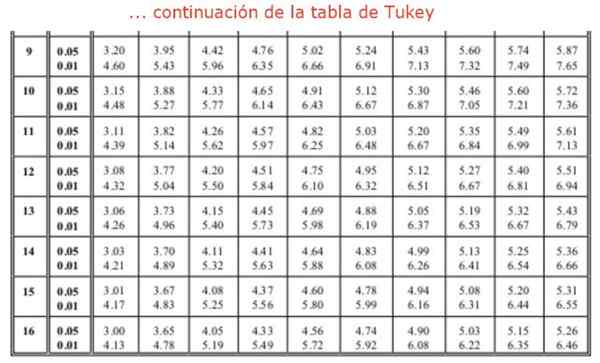
Kjer je faktor q Dobimo iz tabele (Tukey Tabela), ki je sestavljena iz vrst vrednosti q Za različno število zdravljenja ali poskusov. Stolpci označujejo vrednost faktorja q Za različne stopnje svobode. Običajno imajo razpoložljive tabele relativna sredstva 0.05 in 0.01.

Vam lahko služi: do vrstice: formula in enačbe, zastopanost, primeri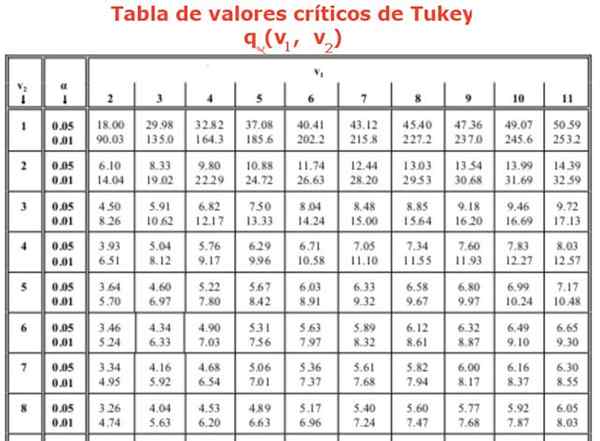

V tej formuli se znotraj kvadratnega korena pojavi faktor MSE (povprečni kvadrat napake), deljen z r, kar kaže na število ponovitev. MSE je število, ki ga običajno dobimo z analizo odstopanj (ANOVA).

Ko razlika med dvema povprečnimi vrednostmi presega vrednost W (Tukey primerjalnik), potem je ugotovljeno, da gre za različna povprečja, če pa je razlika manjša od Tukeyjevega števila, potem gre za dva vzorca s statistično enake povprečne vrednosti.

Številka W je znana tudi kot HSD številka (pošteno pomembna razlika).

To samo številko primerjalnika je mogoče uporabiti, če je število vzorcev, ki se uporabljajo za preskus vsakega zdravljenja.

Neuravnoteženi poskusi

Kadar je iz nekega razloga velikost vzorcev pri vsaki obdelavi drugačna, da se primerja, potem se zgoraj opisani postopek nekoliko razlikuje in je znan kot Test Tukey-Kramer.

Zdaj je pridobljena številka W Primerjava za vsak par tretmajev Jaz, j:

w (i, j) = q √ (½ mse /(ri +rj))

V tej formuli je faktor, ki ga dobimo iz Tukey tabele. Omenjeni dejavnik, ki je odvisen od števila zdravljenja in stopnje svobode napak. r_Yo To je število ponovitev pri zdravljenju I, medtem ko je r_J To je število ponovitev v zdravljenju z J.

Primer

Rejnik zajcev želi narediti zanesljivo statistično študijo, ki kaže na to, katera od štirih blagovnih znamk živilskih živil je najučinkovitejša. Za študijo tvori štiri skupine s šestimi meseci in pol zajce, ki so do takrat imele enake prehranske razmere.

Od eksperimenta do prve skupine se imenuje A1, ker se bo hranil s hrano blagovne znamke 1, podobno kot v skupini A2, A3 in A4. Zabeležena je miza, kjer se zabeleži povečanje telesne mase (v kilogramih) vsakega vzorca po mesecu hrane z različnimi blagovnimi znamkami hrane, pri čemer dobite naslednje rezultate: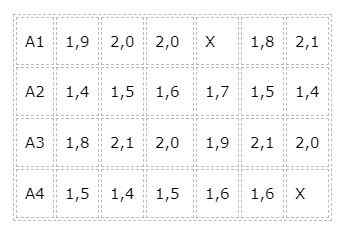Čeprav se je začelo z uravnoteženim eksperimentom, v smislu, da je bilo število zajcev, na katere bi bilo zdravljenje, enako, poskus ni bilo mogoče končati na ta način.

Vam lahko služi: negativna homotecia

Razlogi so bili v tem, da so se v skupinah A1 in A4 smrti pojavile zaradi vzrokov, ki jih ni mogoče pripisati hrani, saj je bila ena od zajcev sekana žuželka, v drugem primeru pa je bila smrt zagotovo vzrok prirojene napake. Tako da so skupine neuravnotežene in potem je treba uporabiti test Tukey-Kramer.

Vaja rešena

Da ne bi preveč razširili izračunov, bo primer uravnoteženega eksperimenta sprejet kot rešena vaja. Kot podatki bodo vzeti naslednje:

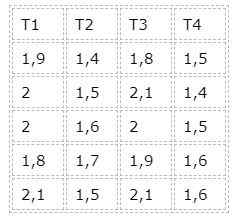
V tem primeru obstajajo štiri skupine, ki ustrezajo štirim različnim načinom zdravljenja. Vendar opažamo, da imajo vse skupine enako število podatkov, zato je potem uravnotežen primer.

Za izvedbo analize ANOVA je orodje, ki je vključeno v preglednico Libreoffice. Druge preglednice, kot so Excel Imajo to orodje za vključeno analizo podatkov. Spodaj je povzetek tabele, ki je nastala po analizi variance (ANOVA):

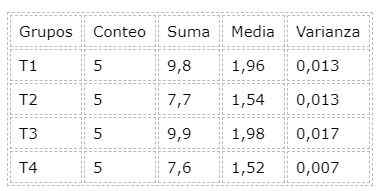
Iz analize variance obstaja tudi vrednost p, ki je na primer 2,24e-6 precej pod 0.05 stopnje pomembnosti, kar neposredno vodi do zavračanja ničelne hipoteze: vsa zdravljenja so enaka. 

To je, med zdravljenjem imajo nekatere različne povprečne vrednosti, vendar morate s statističnim vidikom vedeti, kaj so pomembni in pošteno različni (HSD).

Če želite najti tudi številko W ali kot je znana številka HSD, potrebujemo povprečni kvadrat napake MSE. Iz analize ANOVA je ugotovljeno, da je vsota kvadratov znotraj skupin SS = 0,2; In število stopenj svobode znotraj skupin je df = 16 S temi podatki lahko najdemo MSE:

Vam lahko služi: papomudas

MSE = SS/DF = 0,2/16 = 0,0125

Prav tako je treba najti faktor q Tukeyja, z uporabo tabele. Iščemo v stolpcu 4, ki ustreza štirim skupinam ali zdravljenjem za primerjavo in vrstico 16, saj je analiza ANOVA pokazala 16 stopinj svobode znotraj skupin. To nas vodi do vrednosti q, ki je enaka: Q = 4,33 kar ustreza 0,05 pomembnosti ali 95% zanesljivosti. Končno najdemo vrednost za "pošteno pomembne razlike":

W = hsd = Q √ (MSE /R) = 4,33 √ (0,0125 /5) = 0,2165

Če želite vedeti, kaj so pošteno različne skupine ali zdravljenje, morate vedeti povprečje vsakega zdravljenja:

Prav tako je treba vedeti razlike med povprečnimi vrednostmi parov zdravljenja, ki so prikazane v naslednji tabeli:

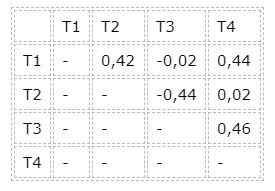T3 in T1 skupini ter skupinam T2 in T4 sta enakih rezultatov. Torej so pošteno različne skupine skupine T1 in T2 ali T3 in T4, saj razlika v njihovih povprečnih vrednostih presega vrednost HSM v Tukeyjevem testu.

Ugotovljeno je, da sta najboljši tretmaji v smislu maksimiranja rezultata T1 ali T3, ki sta ravnodušni s statističnega vidika. Če želite izbirati med T1 in T3, je treba iskati druge dejavnike zunaj predstavljene analize. Na primer cena, razpoložljivost itd.

Reference

1. Cochran William in Cox Gertrude. 1974. Eksperimentalni modeli. Trillas. Mehika. Tretji ponatis. 661p.
2. Snedecor, g.W. In Cochran, w.G. 1980. Statistične metode. Sedmi izd. Iowa, Iowa State University Press. 507p.
3. Jeklo, r.G.D. In Torrie, J.H. 1980. Načela in postopki statistike: biometrični pristop (2. izd.). McGraw-Hill, New York. 629p.
4. Tukey, J. W. 1949. Posameznik, ki primerja sredstva pri analizi variance. Biometrics, 5: 99-114.
5. Wikipedija. Tukeyev test. Pridobljeno iz: v.Wikipedija.com