Formule za določanje koeficientov, izračun, razlaga, primeri

On Koeficient določanja To je številka med 0 in 1, ki predstavlja del točk (x, y), ki sledijo prilagoditveni črti z regresijo nabora podatkov z dvema spremenljivkama.

Znan je tudi kot Prilagoditvena dobrota in ga označuje R². Če ga želite izračunati, se količnik vzame med odstopanjem podatkov ŷi, ocenjenih z regresijskim modelom, in odstopanjem podatkov YI, ki ustreza vsakemu Xi podatkov.

R² = Sŷ / sy

Slika 1. Koeficient korelacije za štiri podatkovne pare. Vir: f. Zapata.

Če je 100% podatkov na regresijski funkcijski liniji, bo koeficient določanja 1.

Nasprotno, če za nabor podatkov in določeno funkcijo prilagoditve, R koeficient r² Izkazalo se je, da je enak 0.5, potem lahko rečemo, da je prilagoditev zadovoljiva ali dobra pri 50%. 

Podobno, ko regresijski model vrže vrednosti r² manj kot 0.5, to kaže, da se izbrana funkcija prilagoditve ne prilagaja zadovoljivo na podatke, zato je potrebna za iskanje druge funkcije prilagoditve.

In kdaj kovariance ali korelacijski koeficient Se nagiba na nič, potem spremenljivke x in y iz podatkov nista povezana in zato r² bo tudi na nič.

[TOC]

Kako izračunati koeficient določanja?

V prejšnjem razdelku je bilo rečeno, da se koeficient določanja izračuna z iskanjem količnika med odstopanjem:

-Ocenjeno z regresijsko funkcijo spremenljivke in 

-Spremenljivka Yi, ki ustreza vsaki od spremenljivke XI. 

V matematični obliki ostaja tako:

R² = Sŷ / sy

Iz te formule izhaja, da r² predstavlja delež variance, razloženo z regresijskim modelom. Lahko pa izračunamo r² Skozi naslednjo formulo, popolnoma enakovredno prejšnji:

R² = 1 - (sε / sy)

Kadar Sε predstavlja odstopanje odpadkov εi = ŷi - yi, medtem ko je SY varianta nabora podatkov podatkov podatkov. Za določitev ŷi se uporablja regresijska funkcija, kar pomeni potrditev, da je ŷi = f (xi).

Lahko vam služi: frakcija, enakovredna 3/5 (rešitev in razlaga)

Varianta nabora podatkov Yi, pri čemer se I od 1 do N izračuna na ta način:

Sy = [σ (yi -)² ) / (N-1)]

In nato nadaljujte na podoben način za Sŷ ali za Sε.

Ilustrativni primer

S prikazom podrobnosti o načinu izračuna Koeficient določanja Vzeli bomo naslednji niz štirih parov podatkov: 

(X, y): (1, 1); (23); (3, 6) in (4, 7).

Za ta nabor podatkov je predlagana linearna regresijska prilagoditev, pridobljena z metodo kvadratnih minimalnih:

f (x) = 2.1 x - 1 

Pri uporabi te funkcije nastavitve dobimo vrstnike:

(X, ŷ): (1, 1.1); (23.2); (3, 5.3) in (4, 7.4).

Nato izračunamo aritmetično srednjo vrednost za x in y:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Variance Sy

Sy = [(1 - 4.25)² + (3. 4.25)² + (6 - 4.25)² +.. ... .(7 - 4.25)²] / (4-1) =

= [-3.25)²+ (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.583

Variance sŷ

Sŷ = [(1.1 - 4.25)² + (3.2 - 4.25)² + (5.3. 4.25)² +.. ... .(7.4 - 4.25)²] / (4-1) =

= [-3.25)² + (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.35

Koeficient določitve r²

R² = Sŷ / sy = 7.35/7.58 = 0.97

Interpretacija

Izkazalo se je, da je koeficient določitve za ilustrativni primer, obravnavan v prejšnjem segmentu.98. To pomeni, da je linearna nastavitev s funkcijo:

 f (x) = 2.1x - 1

98% je zanesljivo razložiti podatke, s katerimi je bil pridobljen z najmanjšo kvadratno metodo. 

Poleg koeficienta določanja obstaja tudi Linearni koeficient korelacije ali tudi znan kot Pearsonov koeficient. Ta koeficient, označen kot r, Izračuna se z naslednjim razmerjem:

R = sxy / (sx sy)

Tukaj števec predstavlja kovarianco med spremenljivkami x in y, imenovalec pa je produkt standardnega odklona za spremenljivo x in standardni odklon za spremenljivko in.

Pearsonov koeficient lahko vzame vrednosti med -1 in +1. Ko se ta koeficient nagiba k +1, obstaja neposredna linearna korelacija med x in y. Če se namesto tega nagiba k -1, obstaja linearna korelacija, ko pa X raste in se zmanjša. Končno je blizu 0 Med obema spremenljivkama ni povezave.

Vam lahko služi: razvrščeni podatki: primeri in rešeni vaja

Treba je opozoriti, da koeficient določanja sovpada s kvadratom Pearsonovega koeficienta, le če je bil prvi izračunan na podlagi linearne nastavitve, vendar ta enakost ni veljavna za druge ne -linearne prilagoditve.

Primeri

- Primer 1

Skupina srednješolcev namerava določiti empirični zakon za obdobje nihala kot funkcijo njegove dolžine. Da bi dosegli ta cilj, naredijo vrsto meritev, v katerih merijo čas nihanja nihanja za različne dolžine in pridobijo naslednje vrednosti:

Dolžina (m)	Obdobje
0,1	0,6
0,4	1.31
0,7	1,78
1	1,93
1.3	2.19
1.6	2.66
1.9	2.77
3	3.62

Zahteva se, da naredi graf disperzije podatkov in z regresijo linearno prilagoditev. Poleg tega pokažite regresijsko enačbo in njegov koeficient določanja.

Rešitev

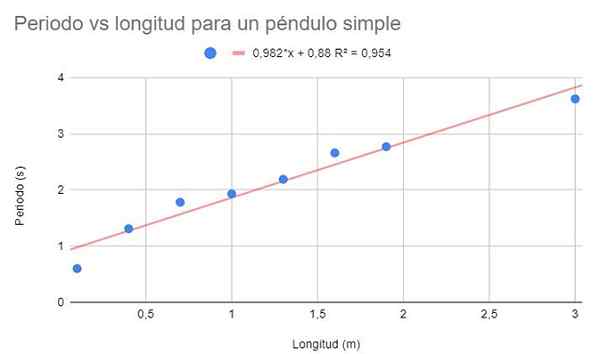Slika 2. Grafična rešitev vaje 1. Vir: f. Zapata.

Opazimo lahko dokaj visok koeficient določanja (95%), zato bi lahko mislili, da je linearna prilagoditev optimalna. Če pa točke opazimo skupaj, se zdi, da imajo nagnjenost k ukrivitvi. Ta podrobnost ni predvidena v linearnem modelu.

- Primer 2

Za iste podatke iz primera 1 naredite tabelo za disperzijo podatkov. Ob tej priložnosti se za razliko od primera 1 zahteva, da se s potencialno funkcijo prilagodi regresijsko prilagoditev.

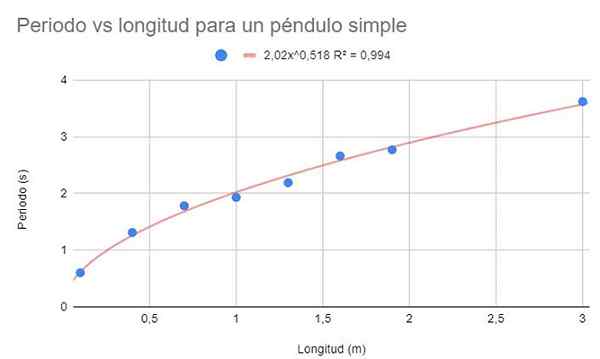Slika 3. Grafična rešitev vadbe 2. Vir: f. Zapata.

Prikažite tudi funkcijo prilagajanja in njegov R -determinacijski koeficient².

Rešitev

Potencialna funkcija je oblike f (x) = sekira^B, kjer sta A in B konstantna, ki sta določena z minimalno kvadratno metodo.

Prejšnja slika prikazuje potencialno funkcijo in njene parametre ter koeficient določanja z zelo visoko vrednostjo 99%. Upoštevajte, da podatki sledijo ukrivljenosti linije trenda.

Vam lahko služi: načelo aditiva

- Primer 3

Z enakimi podatki iz primera 1 in primera 2 naredite drugo -stopinjsko prilagoditev polinoma. Prikažite graf, nastavitveni polinom in koeficient določanja r² dopisnik.

Rešitev

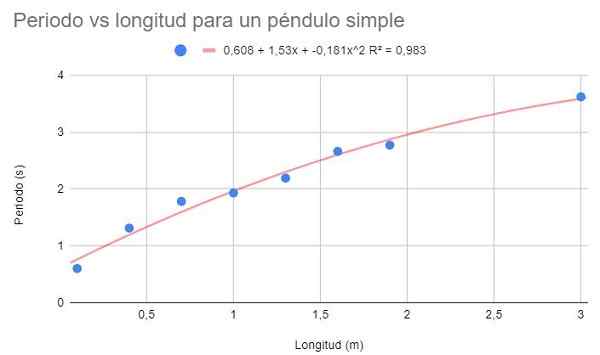Slika 4. Grafična vaja 3 graf. Vir: f. Zapata.

S pomočjo polinoma druge stopnje je mogoče opaziti trend, ki se dobro prilega ukrivljenosti podatkov. Prav tako je koeficient določanja nad linearno nastavitev in pod potencialno nastavitev.

Primerjava prilagoditve

Od treh prikazanih prilagoditev je ena z višjim koeficientom določanja potencialne prilagoditve (primer 2).

Potencialna prilagoditev sovpada s fizično teorijo nihala, ki, kot je znano gravitacije.

Ta vrsta potencialne prilagoditve ne le najvišji koeficient določanja, ampak konstanta eksponenta in sorazmernosti sovpada s fizičnim modelom. 

Zaključki

-Regresijska prilagoditev določa parametre funkcije, katerih cilj je razložiti podatke z minimalno kvadratno metodo. Ta metoda je sestavljena iz zmanjšanja vsote kvadratne razlike med vrednostjo in prilagoditvijo ter vrednostjo YI za podatke XI vrednosti podatkov. Na ta način se določijo parametri funkcije prilagoditve.

-Kot smo videli, je najpogostejša funkcija prilagoditve črta, vendar ni edina, saj so prilagoditve lahko tudi polinomne, potencialne, eksponentne, logaritme in druge. 

-Vsekakor je koeficient določanja odvisen od podatkov in vrste prilagoditve in je kaže na dobroto uporabljene prilagoditve.

-Končno koeficient določanja kaže na odstotek skupne spremenljivosti med vrednostjo in podatki glede na vrednost ŷ vrednost prilagoditve za x.

Reference

1. González c. Splošna statistika. Okreval od: Tarwi.La Molina.Edu.pe
2. IAC. Aragonski inštitut za zdravstvene vede. Pridobljeno iz: ICS-Aragon.com
3. Salazar c. in Castillo s. Načela osnovne statistike. (2018). Pridobljeno iz: dspace.Uce.Edu.Ec
4. Superprof. Koeficient določanja. Okrevano od: Superprof.je
5. USAC. Priročnik za opisne statistike. (2011). Iztegnjeno od: statistike.inženiring.USAC.Edu.Gt.
6. Wikipedija. Koeficient določanja. Okrevano od: je.Wikipedija.com.