Kvadratna prizma

Pojasnjujemo, kaj je štirikolesna prizma, njegove značilnosti, obraze, vrhove, robove, kako izračunati količino, primere in vaje razrešene

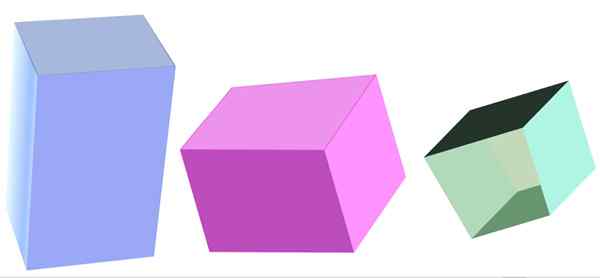
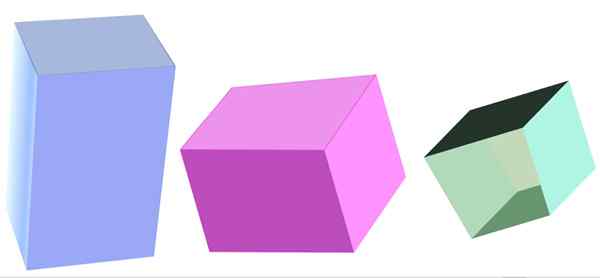Različne vrste štirikolesne prizme. Vir: f. Zapata

Kaj je štirikotna prizma?

On Kvadratna prizma Gre za tridimenzionalno geometrijsko figuro družine Polyhedros. Sestavljen je iz dveh enakih in vzporednih obrazov, z obliko štirikotnika kot baze in štirimi paralelogrami na straneh, za skupno šest obrazov.

Obstaja več meril za njihovo razvrščanje, saj obstaja veliko možnosti za obliko obrazov in naklona. Na primer obstajajo Naravne domače prizme in Nagnjene štirikolesne prizme.

V prvem primeru so stranice pravokotne na podlago, nato pa so pravokotniki ali kvadratki. V drugem primeru so stranski obrazi nagnjeni glede na osnovo, zato jih ne morejo biti pravokotniki ali kvadratni.

Poleg tega je lahko štirikolesna prizma redna ali nepravilna, odvisno od baze je reden ali nepravilen štirikolesnik. Redni štirikolesnik je kvadrat, katerega štiri strani in njegovi štirje koti merijo isto .

Primer posebne domače prizme je paralelipiped, katerih baze so paralelogrami. Oblike škatel in opeke so navdihnjene s štirikolesnimi prizmami, zato so dobri primeri uporabe te geometrijske figure v praktičnih aplikacijah.

Značilnosti štirikolesne prizme

Med najpomembnejšimi značilnostmi štirikolesne prizme so naslednje:

• Njihovi obrazi imajo poligonsko obliko.
• Skupaj ima 6 obrazov (2 baze in 4 strani), 12 robov ali robov in 8 vrhov (vogalov).
• Stranske obraze so lahko oblikovane kot: kvadrat, pravokotnik, paralelogram, rombo ali romboid.
• Njene stranice so lahko ravne (oblikujejo 90 ° kot z osnovami) ali nagnjene (na notranji strani je kot manj kot 90 °).
• Bočni obrazi ravnih prizm so lahko samo kvadratni ali pravokotniki.
• Baze prizme prejmejo tudi ime smernice.
• Če je osnova redna štirikolesnica, je tudi kvadratna prizma redna tudi. Ker je ravna figura redna, če imajo vse njegove strani enak ukrep, je edina možnost, da so baze kvadratne.
• Ko je osnova prizme kateri koli drug štirikolesnik, ki se razlikuje od kvadrata, potem se prizma šteje za nepravilno.
• Navadna štirikolesna prizma je mogoče registrirati v jeklenki.

Vam lahko služi: inferencialna statistika: zgodovina, značilnosti, za kaj je, primeri

Elementi štirikolesne prizme

Pet elementov štirikolesne prizme je skupno vsem prizmom:

• Baze, sestavljata dva enaka in vzporedna kvadrilatela.
• Stranski obrazi, so štirje paralelogrami, ki mejijo na številko.
• Točke ali vogali, skupne točke, ki imajo tri sosednje strani prizme.
• Robovi ali robovi, skupni segment, ki imata dva sosednja obraza.
• Višina: To je dolžina pravokotnega segmenta s konci v osnovah. Ko je prizma ravna, višina sovpada z mero stranskih robov.
• Neposredni odsek, območje presečišča med prizmo in ravnino, ki tvori 90 ° s stranskimi robovi.

Naslednja slika prikazuje vsak od teh elementov za ravno štirikolesno prizmo:

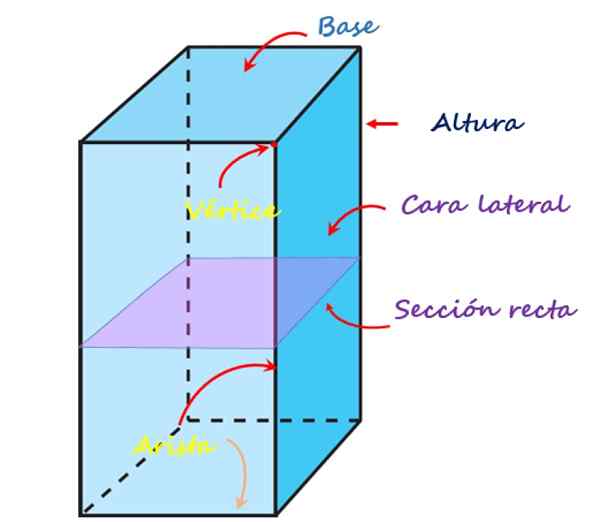Elementi štirikolesne prizme. Vir: f. Zapata

Obrazi, vrhovi in ​​robovi

Zelo pomembno za preučevanje štirikolesne prizme so obrazi, vrhovi in ​​robovi:

Obraze

Obrazi prizme naredijo skupno 6: dve enaki podlagi v obliki štirikolesnikov in 4 stranskih strani ali obrazov v obliki paralelograma.

Točke

So vogali figure, točka, kjer prihajajo trije sosednji obrazi.

Robovi

So presečilni segmenti med prizmo obrazi. Robovi so razvrščeni kot:

• Osnovni robovi, Skupni segmenti med bazami in stranskimi obrazi.
• Stranski robovi, Kot že ime pove, so skupni segmenti med stranskimi obrazi.

Zgornja slika prikazuje dve vrsti robov, označenih z različnimi barvnimi puščicami. Število robov n_Do lahko določimo z Eulerjev teorem poliedrosov, ki se nanašajo na število robov na obraze n_C in vrhovi n_V:

Vam lahko služi: matematične funkcije

N_Do = N_C + N_V −2

Za štirikotno prizmo n_C = 6 in n_V = 8, torej:

N_Do = 6 + 8 −2 = 12

Zato je število robov ali robov štirikolesne prizme 12.

Kako izračunati prostornino štirikolesne prizme?

Obseg prizme se razume kot del prostora, ki ga zaklene, in se meri v kubičnih enotah, ki so lahko kubični metri, kubični centimetri, kubični ali drugi primerni, pod pogojem.

Zvezek V je vedno pozitiven znesek, v primeru vsake štirikolesne prizme pa ga daje izdelek med osnovo osnove do_b in višina H:

V = a_b × H

Yo) Redni štirikolesni volumen

Ker so baze kvadratne in kvadrat kvadrata je njegova stran ℓ kvadrat:

Do_b = ℓ²

Nato je glasnost prizme, katere višina je "H":

V = ℓ² × H

Ii) Nepravilen volumen štirikolesne prizme

Odvisno je od oblike osnove in višine "H" prizme:

1.- Pravokotna osnovna prizma

Območje strani pravokotnika "A" in "B" je:

Do_b = A × B

Torej je glasnost:

V = a × b × h

2.- Romboidna osnovna prizma

Območje Rhombusa je pol produkt njegovih diagonalov "D" in "D":

In glasnost je:

3.- Osnovna prizma v obliki romboida

Osnovno območje v obliki romboida je produkt njegove baze "B" in njegove relativne višine "h_r"Na to osnovo, ki je pravokotni segment, ki sega od te osnove do vzporedne strani.

Do_b = B × H_r

Zato je glasnost prizme s to bazo:

Vam lahko služi: kakšen je obseg statistike? (S primeri)

V = b × h_r × H

4.- Trapezna osnovna prizma

Ker je območje trapezoida pol -mesto vzporednih strani "A" in "B", pomnoženo s svojo višino "C":

Volumen trapezoidne prizme je:

5.- Trapezoidna osnovna prizma

Področje simetričnega trapezoida je pol -produkt njegovih diagonalov D ​​in D, zato:

V tem primeru je obseg prizme:

Vaja rešena

Trapezalna osnovna štirikotna prizma ima prostornino 648 cm³. Vzporedne strani trapezoida merijo A = 10 cm in B = 5 cm, višina trapeza pa je c = 6 cm. S temi podatki poiščite višino prizme.

Rešitev

Ker imajo dimenzije baze, lahko vaše območje enostavno izračunate:

In formule:

V = a_b × H

"H" je očiščen, višina prizme, saj je znan njen glasnost:

H = v/ a_b = 648 cm³ / 45 cm² = 14.4 cm

Primeri

Pravokotna prizma ali kocka

Šest obrazov te ravne prizme je kvadratnih ali pravokotnih. Škatle so primeri pravokotnih prizmov, oblike, ki se uporablja tudi v številnih predmeti in konstrukcijah, kot so stavbe.

Kocka

Kocka je običajna štirikotna prizma, katere šest strani so oblikovane kot kvadrat, na primer kocka ali dobro znana Rubikova igra kocka.

Kocka je del skupine platonskih trdnih snovi, geometrijske figure, ki izpolnjujejo dva pogoja. Prva je, da je vsak obraz navaden poligon, drugi pa je, da ima vsaka točka skupno enako število obrazov.

Kocka izpolnjuje oba pogoja, saj imajo njihovi obrazi kvadratno obliko, ki je navaden poligon. In v vsakem od osmih vrhov kocke tri obraze istega konverge.

Preostale platonske trdne snovi so tetraedron, oktaedron, dodekaedro in ikosaedro.