Do linijske formule in enačb, zastopanja, primeri

The nerešena vrstica To je tangenta kota θ, da se ta črta tvori z vodoravno osi, ki se s konvencijo meri v nasprotni smeri do rok ure. Nagib katere koli črte je vedno konstanten in zato je ena najpomembnejših lastnosti.

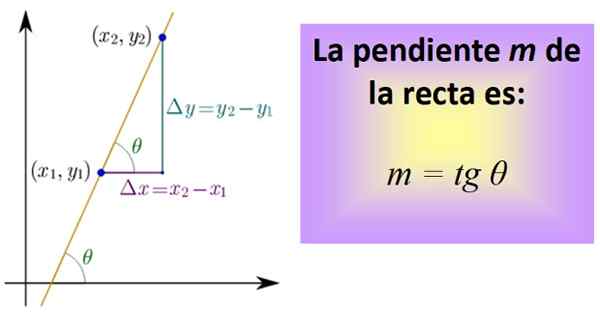
Če ga želite izračunati, morate vedeti dve točki črte, katerih koordinate so (x x₁,in₁) in (x₂,in₂). Med obema točkama je narisan segment, ki spada v črto, nato pa segmenti, ki predstavljajo razdaljo med x, narišejo₁ in x₂, in med in₁ in in₂, Kot na spodnji številki.

Slika 1. Nagib črte je tangenta kota θ. Vir: Wikimedia Commons.

Trije segmenti sestavljajo pravi trikotnik, katerega noge so: Δx = x₂ - x₁  in Δy = in₂ - in₁. Ustrezajo horizontalnemu premiku in drugemu navpičnemu.

Zdaj je definiran količnik, imenovan tangent kota θ in skrajšano tg θ, kar je ravno naklon m vrstice:

m = tg θ = Δy / Δx

Upoštevajte, da za črto ta kot ostaja konstanten, ne glede na točke, ki so bile potrebne za izračun njegove tangente. Vsekakor nam ta vrednost ponuja merilo, kako naklonjena je črta.

Skozi koordinate izbranih točk ostaja formula naklona:

M = (y - y₁ ) / (X₂ - x₁)

[TOC]

Grafični prikaz

Spodaj imamo več situacij, v katerih je koncept naklona pomemben. Njegova vrednost je mogoče enostavno izračunati z merjenjem ustreznega navpičnega in vodoravnega premika, nato pa na začetku navedeno količnik.

To nam daje predstavo o pobočju ali upadu neke strukture, kot so klančina, streha ali cesta:

Vam lahko služi: naključno vzorčenje: metodologija, prednosti, slabosti, primeri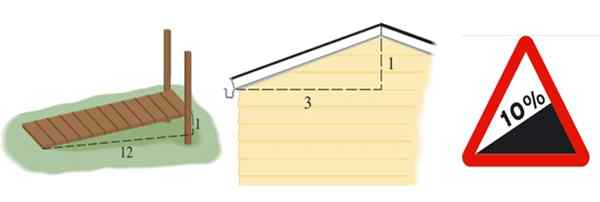 Slika 2. Od leve proti desni pobočje rampe, strehe in pobočja ceste, slednja pa v odstotkih. Vir: Stewart, J. Precáculculo in Wikimedia Commons (desna slika).

Nagib rampe, prikazane na sliki 2 na levi strani, je m = 1/12, streha je m = 1/3 in cesta je izražena v odstotkih. 10 -odstotni odstotek pomeni, da na vsakih 100 metrov, ki napredujejo vodoravno, zaslužijo 10 metrov visoko:

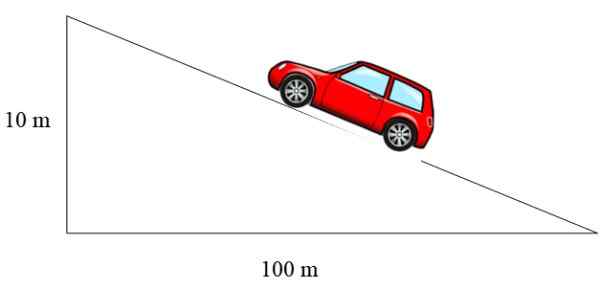Slika 3. Vozilo se dvigne skozi pobočje, katerega pobočje je 10%. Vir: f. Zapata.

V tem primeru je naklon 10/100 = 0.1, ki je izražen kot odstotek, je 10%.

Vrste pobočja

Nagib črte je lahko pozitiven, negativen ali ničen. Na primer, črta, prikazana na sliki 1, ima pozitiven naklon. Takoj cenimo, ker vidimo, da je črta "dvignjena", če jo vidimo od leve proti desni.

Če se črta spusti od leve proti desni. In ko je črta vodoravna, je njen naklon ničen.

Končno za navpične črte naklon ni definiran.

Grafični prikaz vsake vrste je spodaj:

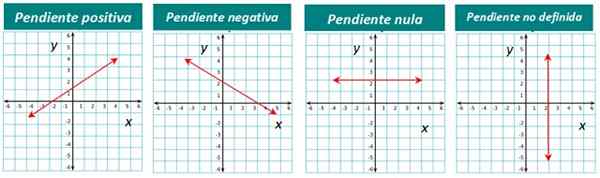Slika 4. Vrstice glede na pobočje. Vir: f. Zapata.

Kako se naklon izračuna črta?

Izračun naklona je zelo preprost, preprosto morate najti navpično premik in vodoravno premik, nato.

Ko imate risbo črte v kartezijanski ravnini, ti premiki izbirajo katero koli dve točki črte P₁ In p₂, Določitev njihovih koordinat in uporaba definicije, podane na začetku:

Vam lahko služi: kaj predstavlja dolžino premika šesterokotnika

M = (y - y₁ ) / (X₂ - x₁ )

Ker je vrednost pobočja neodvisna od izbire P₁ In p₂ , Izbrali bomo točko P koordinat (x, y), ki spada v črto, katerih koordinate niso znane, in druga točka P₁ katerih koordinate so: (x₁,in₁).

Pobočje je:

M = (y - y₁) / (x - x₁)

Lahko razčistimo in:

in - in₁ = m (x - x₁)

Zdaj predpostavimo, da je točka p₁ To je presečišče črte z navpično osi koordinat (0, b). Nadomestitev tega v prejšnji enačbi:

in - b = m (x - 0) → y = mx + b

Ta izraz je znan kot enačba črte v obliki V teku - križišče, Ker je črta nedvoumno določena, ko sta znana naklon in križišče z navpično osi.

Če poznate samo naklon, ni dovolj za karakterizacijo črte na ravnini, saj bi lahko Infinite Straight imel enak naklon, kar pomeni, da so vzporedni, vendar pojdite skozi druge točke.

Rešene vaje

- Vaja 1

Poiščite naklon črte, prikazane na naslednji sliki:

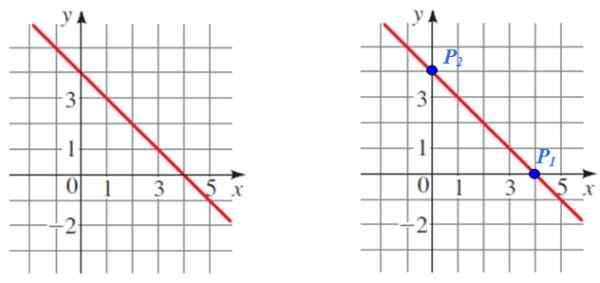Slika 5. Skozi graf črte sta izbrani dve točki za izračun njegovega naklona. Vir: f. Zapata.

Rešitev

Str₁ In p₂ Gre za dve točki, ki sta enostavna za prebrano.

Koordinate vsake točke so:

Str₁ (4.0) in P₂ (0,4)

Z zamenjavo enačbe naklona:

M = (4 - 0) / (0 - 4) = 4 / ( - 4) = -1

Nagib je negativen, kar je bilo pričakovati po opazovanju grafike.

Vam lahko služi: kompleksne številke: lastnosti, primeri, operacije

- Vaja 2

Poiščite enačbo vrstice, ki poteka skozi točko (1, -6) in je vzporedna s črto y = 2x - 3.

Rešitev

Nagib iskane črte mora biti enak kot pri y = 2x - 3, saj so vzporedni. Za to vrstico je naklon M = 2, zato je tisti, ki ga iščemo, obrazec:

in - in₁ = 2 (x - x₁)

Zdaj nadomestimo točko, skozi katero prehaja naša črta: x₁ = 1 in₁ = -6.

in - (-6) = 2 (x - 1)

Zato y = 2x - 2 - 6 → y = 2x - 8

Primeri

Dve količini sta lahko povezana tako, da je vaš graf ravno črta. V tem primeru se reče, da imajo zneski linearno odvisnost in naklon črte je mogoče razlagati kot razlog za spremembo ene spremenljivke v drugo.

Primer 1

Recimo, da je bazen napolnjen z vodo oceniti konstantno v času. Seveda več časa mineva, več vode je shranjena. No, hitrost, ki ji je bazen zapolnjen, je natančno naklon črte, ki povezuje glasnost do časa:

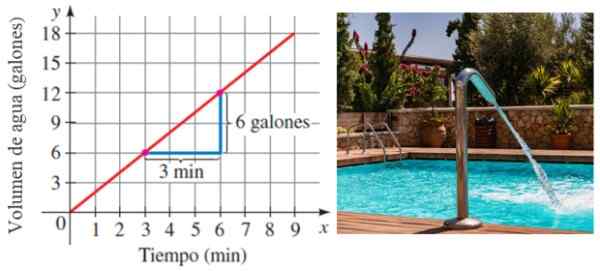Slika 6. Naklon kot razlog za spremembe. Vir: Stewart, J./Pxfuel.

V tem primeru je bazen napolnjen s hitrostjo 6/3 litrov na minuto ali 2 litra/minuto.

Primer 2

Ko se mobilni telefon premakne v ravni črti s konstantno hitrostjo, je naklon grafa položaja odvisen od časa, ni nič drugega kot omenjena hitrost. Graf prikazuje mobilni telefon s pozitivno hitrostjo, kar pomeni, da se oddalji od izvora.

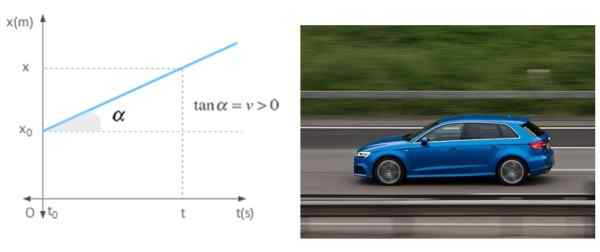Slika 7. Nagib grafa v primerjavi s časom je hitrost mobilnega telefona v enakomernem pravokotnem gibanju. Vir: Wikimedia Commons/Pixabay.

Reference

1. Alvarez, J. Pobočje ceste. Okreval od: geogebra.je.
2. Carena, m. 2019. Priročnik za matematiko prednavdljivosti. Nacionalna univerza na obali.
3. Hoffman, J. Izbira vprašanj matematike. Zvezek 4.
4. Jiménez, r. 2008. Algebra. Dvorana Prentice.
5. Stewart, J. 2006. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.
6. Zill, d. 1984. Algebra in trigonometrija. McGraw Hill.