Značilne primere, primeri, vaje

The praštevila, Imenujejo se tudi absolutni bratranci, so tista naravna številka, ki jih je med seboj samo debelo in 1. V tej kategoriji številke, kot so: 2, 3, 5, 7, 11, 13, 17, 19, 23 in še veliko več prihajajo v to kategorijo.

Po drugi strani je sestavljena številka deljiva sama po sebi, za 1 in vsaj še eno številko. Imamo na primer 12, kar je deljivo za 1, 2, 4, 6 in 12. Po konvenciji 1 ni vključen na seznam primerov ali v spojine.

Slika 1. Nekaj ​​glavnih številk. Vir: Wikimedia Commons.

Poznavanje glavnih številk izhaja iz oddaljenih časov; Stari Egipčani so z njimi že obvladali in so bili zagotovo znani že veliko prej.

Te številke so zelo pomembne, saj lahko vsako naravno število predstavlja produkt osnovnih številk, saj je ta edinstvena predstavitev, razen po vrstnem redu dejavnikov.

To dejstvo je v celoti vzpostavljeno v teoremu, imenovanem Temeljni teorem aritmetike, ki navaja, da so številke, ki niso bratranci, nujno sestavljene iz številk, ki so.

[TOC]

Značilnosti glavnih številk

Pod glavnih značilnostih glavnih številk:

-So neskončni, saj je vedno mogoče najti veliko prvo številko.

-Če je prva številka str se ne deli natančno na drugo številko do, Nato se reče str in do Med seboj so bratranci. Ko se to zgodi, je edini skupni delitelj 1 1.

Ni potrebno do Biti absolutni bratranec. Na primer, 5 je bratranec, in čeprav 12 ni, sta obe številki bratranca med seboj, saj imata oba skupni delitelj na 1.

-Ko je glavna številka str Razdelite moč številke n, Deli tudi a n. Razmislite o 100, kar je moč 10, natančneje 10². Zgodi se, da dva delita 100 in 10.

-Vse glavne številke so nenavadne, razen 2, zato je njihova zadnja številka 1, 3, 7 ali 9. 5 ni vključeno, ker čeprav je čuden in bratranec, nikoli ni končna številka druge prvotne številke. Pravzaprav so vse številke, ki se končajo v 5.

Vam lahko služi: centralna simetrija: lastnosti, primeri in vaje

-Ja str Je bratranec in delitelj izdelka dveh številk do.b, tako str deli enega od njih. Na primer, prvo številko 3 deli izdelek 9 x 11 = 99, saj je 3 delitelj 9.

Kako vedeti, ali je številka bratranec

The Prvinskost To je ime kakovosti biti bratranec. No, francosko matematiko Fermatov mali izrek, To pravi:

"Glede na sestrično naravno številko str in katero koli naravno številko do večji od 0, se to izpolni do^str - do Je večkratnik str, dokler str biti bratranec ".

To lahko potrdimo z majhnimi številkami, na primer P = 4, Da že vemo, da ni bratranec in a = 6:

6⁴ - 6 = 1296 - 6 = 1290

Številka 1290 ni ravno deljiva med 4, zato 4 ni glavna številka.

Naredimo test zdaj s p = 5, ki je bratranec in a = 6:

6⁵ - 6 = 7766 - 6 = 7760

7760 je deljiv med 5, saj je poljubno število, ki se konča pri 0 ali 5. V resnici 7760/5 = 1554. Ker je Fermatov mali teorem izpolnjen, lahko zagotovimo, da je 5 glavna številka.

Test skozi teorem je učinkovit in neposreden z majhnimi številkami, v katerem je operacija enostavno izvesti, a kaj storiti, če nas prosijo, da ugotovimo prvotnost velikega števila?

V tem primeru je številka zaporedno razdeljena med vse manjše številke, dokler ni natančna delitev ali da je količnik manjši od delitve.

Če je katera koli delitev natančna, to pomeni, da je številka sestavljena in če je količnik manjši od delitve, to pomeni, da je številka bratranca. V praksi ga bomo izvedli v letu Rešeni 2.

Načine, kako najti prvo številko

Obstajajo neskončne primere in ni edinstvene formule, ki bi jih določila. Vendar pa opazovanje nekaterih glavnih številk, kot je ta:

Vam lahko služi: NULL kot: definicija in značilnosti, primeri, vaje

3, 7, 31, 127 ..

Opazimo, da so v obliki 2ⁿ - 1, z n = 2, 3, 5, 7, 9 ... Zagotavljamo vam:

2² - 1 = 4 - 1 = 3; 2³ - 1 = 8 - 1 = 7; 2⁵ - 1 = 32 - 1 = 31; 2⁷ - 1 = 128 - 1 = 127

Vendar tega na splošno ne moremo zagotovitiⁿ - 1 Bodite bratranec, ker obstajajo nekatere vrednosti n za katero ne deluje, na primer na 4:

2⁴ - 1 = 16 - 1 = 15

In številka 15 ni bratranec, saj se konča v 5. Vendar pa je ena največjih primerov, ki jih poznamo z računalniškimi izračuni, v obrazcu 2ⁿ - 1 z:

N = 57.885.161

The Formula Mersenne nam zagotavlja, da 2^str - 1 je vedno bratranec, dokler str Bodi tudi bratranec. Na primer, 31 je bratranec, zato je gotovo, da 2³¹ - 1 je tudi:

2³¹ - 1 = 2.147.483.647

Vendar pa formula omogoča določitev le nekaj glavnih številk, ne pa vse.

Eulerjeva formula

Naslednji polinom omogoča iskanje primerov, dokler je N med 0 in 39:

P (n) = n² + N + 41

Kasneje je v razdelku Rešene vaje primer njegove uporabe.

Pregled Eratostenes

Eratóstenes je bil fizika in matematična do starodavne Grčije, ki je živela v tretjem stoletju.C. Izdelal je grafično metodo iskanja najpomembnejših številk, ki jih lahko v praksi uresničimo z majhnimi številkami, imenujemo se zaslon Eratóstenes (zaslon je kot cedilo).

-Številke so postavljene v tabelo, kot je prikazano v animaciji.

-Potem so celo številke označene, razen 2, za katero vemo, da sta bratranec. Vsi drugi so večkratni in zato niso bratranci.

-Označeni so tudi večkratniki 3, 5, 7 in 11, razen vseh, ker vemo, da so bratranci.

-Večkratniki 4, 6, 8, 9 in 10 so že označeni, ker so spojine in so zato večkratni navedeni bratranci.

Vam lahko služi: Zgodovina trigonometrije iz njegovega izvora

-Končno so preostale številke neoznačene.

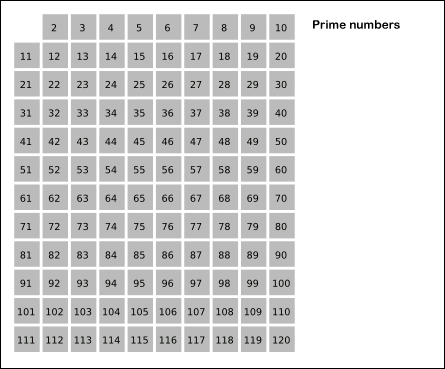Slika 2. Eratostenes presejalna animacija. Vir: Wikimedia Commons.

Vaje

- Vaja 1

Uporaba eulerjevega polinoma za primere poiščite 3 številke, večje od 100.

Rešitev

To je polinom, ki ga je Euler predlagal, da bi našel primere, ki delujejo za n vrednosti med 0 in 39.

P (n) = n² + N + 41

Preko tanteo izberemo vrednost N, na primer n = 8:

P (8) = 8² + 8 + 41 = 113

Ker n = 8 ustvari prvotno številko, večjo od 100, potem ocenimo polinom za n = 9 in n = 10:

P (9) = 9² + 9 + 41 = 131

P (10) = 10² + 10 + 41 = 151

- Vaja 2

Ugotovite, ali so naslednje številke bratranci:

a) 13

b) 191

Rešitev

13 je dovolj majhno, da lahko uporabi Fermatov mali izrek in pomoč kalkulatorja.

Uporabljamo A = 2 tako, da številke niso prevelike, čeprav jih je mogoče uporabiti tudi A = 3, 4 ali 5:

2¹³ - 2 = 8190

8190 je deljiv med 2, saj je celo, zato je 13 bratranca. Bralec ga lahko potrdi tako, da opravi isti test z a = 3.

Rešitev b

191 je zelo velik za preizkus izrek in skupni kalkulator, vendar lahko delimo med vsako prvo številko. Izpustimo, da se razdelimo na 2, ker 191 sploh ni in delitev ne bo natančna ali razmerje manj kot 2.

Poskusili smo razdeliti do 3:

191/3 = 63.666…

In ne daje natančno, niti količnik ni manjši od delitve (63,666 ... je večji od 3)

Še naprej preizkušamo 191 s strani Cousins ​​5, 7, 11, 13 in natančna delitev ni dosežena niti razmerje manj kot delitelj. Dokler se ne deli med 17:

191/17 = 11, 2352 ..

Ker ni natančen in 11.2352 ... je manj kot 17, številka 191 je bratranec.

Reference

1. Baldor, a. 1986. Aritmetika. Codex izdaje in distribucije.
2. Prieto, c. Primo številke. Pridobljeno z: strani.Matem.Ne.mx.
3. Lastnosti glavnih številk. Okreval od: mae.Ufl.Edu.
4. SmartIck. Primo številke: kako jih najti s sito eratostenov. Okrevano od: SmartIck.je.
5. Wikipedija. praštevilo. Okrevano od: je.Wikipedija.org.