Lastnosti zapletenih številk, primeri, operacije

The zapletene številke So številčni niz, ki pokriva realne številke in vse korenine polinomov, vključno s celo koreninami negativnih številk. Te korenine ne obstajajo v naboru resničnih števil, toda v zapletenih številkah je rešitev.

Kompleksna številka je sestavljena iz resničnega dela in drugega, imenovanega "namišljena". Pravi del se imenuje do, Na primer in namišljeni del Ib, z do in b resnične številke in "mi je všeč Namišljena enota. Na ta način je v obliki zapletene številke:

Z = a + ib

Slika 1.- Binomski prikaz zapletene številke v smislu resničnega dela in namišljenega dela. Vir: Pixabay.

Primeri zapletenih števil so 2 - 3i, -πi, 1 + (1/2) i. Toda preden delujemo z njimi, poglejmo, od kod izvira namišljena enota Yo, Glede na to kvadratno enačbo:

x² - 10x + 34 = 0

V katerem je a = 1, b = -10 in c = 34.

Ko se za določitev rešitve uporabi formula topila, najdemo naslednje:

Kako določiti vrednost √-36? Ni resničnega števila, da je kvadrat negativni znesek. Potem je sklenjeno, da ta enačba nima resničnih rešitev.

Vendar lahko to napišemo:

√-36 = √-6² = √6² (-1) = 6√-1

Če določimo določeno vrednost x takšno, da:

x² = -1

Tako:

x = ± √-1

In prejšnja enačba bi imela rešitev. Zato je bila namišljena enota opredeljena kot:

I = √-1

In tako:

√-36 = 6i

Številni matematiki antike so delali na reševanju podobnih težav, pri čemer so poudarili renesančni Girolamo Cardano (1501-1576), Nicolo Fontana (1501-1557) in Raffaele Bomballi (1526-1572).

Leta kasneje René Descartes (1596-1650), imenovan "namišljen" za količine, kot je √-36 primera. Zaradi tega je √-1 znan kot Namišljena enota.

[TOC]

Lastnosti zapletenih številk

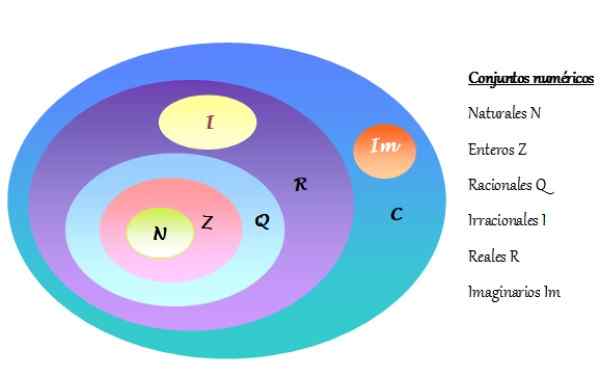
-Nabor zapletenih številk je označen kot C in vključuje realne številke r in namišljene številke IM. Numerični sklopi so predstavljeni v Vennovem diagramu, kot je prikazano na naslednji sliki:

Vam lahko služi: rešene faktorizacijske vaje Slika 2. Vennov diagram numeričnih sklopov. Vir: f. Zapata.

-Vsaka zapletena številka je sestavljena iz enega resničnega dela in drugega namišljenega dela.

-Ko je namišljeni del zapletene številke 0, je to čisto resnično število.

-Če je resnični del zapletene številke 0, potem je številka čista namišljena.

-Dve zapleteni številki sta enaki, če sta njun resnični del in namišljeni del enak.

-S kompleksnimi številkami se izvajajo znane operacije vsot, odštevanje, množenje, izdelek in opolnomočenje, kar ima za posledico drugo zapleteno število.

Predstavitev zapletenih številk

Kompleksne številke je mogoče predstaviti na različne načine. Tu so glavne:

- Binomna oblika

To je dana oblika na začetku, kjer z je zapletena številka, do je pravi del, b je namišljen del in Yo To je namišljena enota:

Z = a + ib

Ali tudi:

Z = x + iy

Eden od načinov za grafiko kompleksne številke je skozi kompleksno ravnino, prikazano na tej sliki. Namišljena os je navpična, prava os pa vodoravna in označuje kot re.

Zapletena številka z V tej ravni je predstavljen kot koordinatna točka (X, y) tudi (A, b), Kot je to storjeno s točkami prave ravnine.

Razdalja od izvora do točke z je modul zapletene številke, označen kot r, medtem ko je φ kot, ki se tvori r S pravo osi.

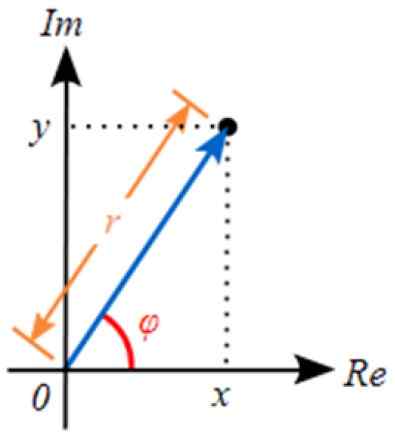
Slika 3. Predstavitev zapletene številke v zapleteni ravnini. Vir: Wikimedia Commons.

Ta predstavitev je tesno povezana z vektorji v resnični ravnini. Vrednost r ustreza modul zapletene številke.

Lahko vam služi: Gauss-Seidel Metoda: Pojasnilo, aplikacije, primeri

- Polarna oblika

Polarna oblika je sestavljena iz izražanja zapletene številke, ki daje vrednosti r in od φ. Če pogledamo sliko, vrednost r Ustreza hipotenusi pravega trikotnika. Kategorije so vredne do in b, O dobro x in in.

V binomni ali binomni obliki se lahko premaknemo na polarno obliko z:

R = √x²+in²

Kot φ To je tisti, ki tvori segment R z vodoravno osi ali namišljeno osi. Znano je kot prepir zapletene številke. Na ta način:

φ = arctg (y/x)

Argument ima neskončne vrednosti, ob upoštevanju, da se vsakič, ko se vrne vrnitev, kar je vredno 2π radianov, R spet zaseda isti položaj. Na ta način je na splošno argument Z, označen z Arg (z), izražen na naslednji način:

Arg (z) = φ + 2kπ

Kjer je k celoten in služi za označevanje količine zavojev: 2, 3, 4 .. . Znak označuje pomen vrtenja, če je narejen čas ali antihorario.

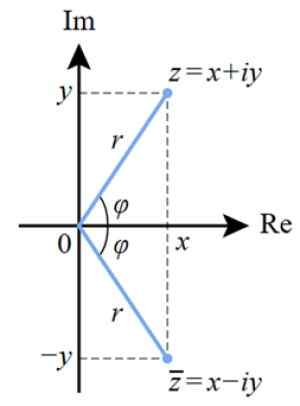
Slika 4. Polarna predstavitev zapletene številke v kompleksni ravnini. Vir: Wikimedia Commons.

In če želimo polarno obliko prenesti v binomno obliko, uporabljamo trigonometrične razloge. Iz prejšnje številke to lahko vidimo:

x = r cos φ

y = r sen φ

Na ta način z = r (cos φ+i sin φ)

To je tako skrajšano:

z = r cis φ

Primeri zapletenih številk

Naslednje kompleksne številke so podane binomno:

a) 3 + i

b) 4

d) -6i

In te v urejenem navoru:

a) (-5, -3)

b) (0, 9)

c) (7.0)

Končno je ta skupina dana polarna ali trigonometrična:

a) √2 cis 45 °

b) √3 cis 30 °

Vam lahko služi: hipergeometrična porazdelitev: formule, enačbe, model

c) 2 cis 315 °

Za kaj so?

Uporabnost zapletenih števil presega ločljivost enačbe druge stopnje, prikazane na začetku, saj so bistvene na področju inženirstva in fizike, zlasti v:

-Študija elektromagnetnih valov

-Nadomestna analiza toka in napetosti

-Modeliranje vseh vrst signalov

-Teorija relativnosti, kjer se čas predpostavlja kot namišljena velikost.

Operacije s kompleksnimi številkami

S kompleksnimi številkami lahko izvajamo vse operacije, ki se izvajajo z resničnim. Nekatere je lažje storiti, če številke pridejo binomno, na primer vsota in odštevanje. Po drugi strani sta množenje in delitev enostavnejše, če se izvajata s polarno obliko.

Poglejmo nekaj primerov:

- Primer 1

Dodaj z₁ = 2 + 5i in z₂ = -3 -8i

Rešitev

Pravi deli se dodajo ločeno od namišljenih delov:

z₁ + z₂ = (2 + 5i) + (-3 -8i) = -1 -3i

- Primer 2

Pomnožite z₁ = 4 cis 45 ° in z₂ = 5 cis 120 °

Rešitev

Lahko je dokazano, da je produkt dveh zapletenih števil v polarnem ali trigonometričnem dano::

z₁ . z₂ = r₁.r₂ Cis (φ₁ + φ₂)

V skladu s tem:

z₁ . z₂ = (4 × 5) cis (45 + 120) = 20 cis 165 °

Aplikacija

Preprosta uporaba zapletenih številk je najti vse korenine polinomne enačbe, kot je tisto, ki je prikazana na začetku članka.

V primeru enačbe x² - 10x + 34 = 0, pri uporabi formule topila dobimo:

Zato so rešitve:

x₁ = 5 + 3i

x₂ = 5 - 3i

Reference

1. Earl, r. Zapletene številke. Okrevano od: matematike.vol.AC.Združeno kraljestvo.
2. Figuera, j. 2000. Matematika 1. Raznovrstno. Co-Bo izdaje.
3. Hoffmann, J. 2005. Izbira vprašanj matematike. Monfort Publications.
4. Jiménez, r. 2008. Algebra. Dvorana Prentice.
5. Wikipedija. Zapletene številke. Pridobljeno iz: v.Wikipedija.org