Celo število številk

Kaj so celotne številke?

Celotne številke predstavljajo niz koristnih številk za štetje celotnih predmetov, ki so in tistih, ki niso. Tudi prešteti tiste na eni strani in drugi na določenem referenčnem kraju.

Tudi s celotnimi številkami lahko odštevanje ali razlike izvedemo med številom in drugo večjo od njega, na primer poravnan kot dolg. Razlikovanje med dobički in dolgovi se izvede z znaki + oziroma -.

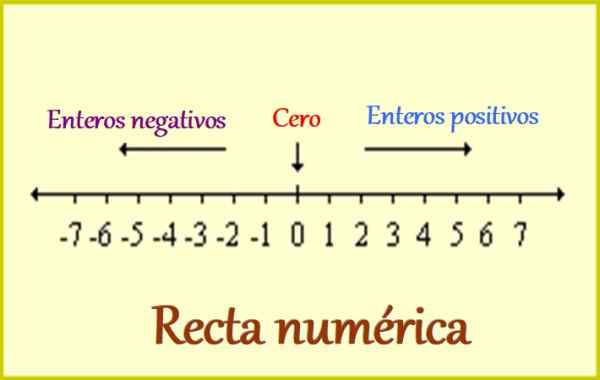
Slika 1. Numerična črta za cele številke. Vir: Wikimedia Commons. LEOMG/CC BY-SA (https: // creativeCommons.Org/licence/by-sa/3.0.

Zato celotne številke vključuje naslednje:

-Pozitivna cela števila, ki so napisana pred znakom +ali preprosto brez znaka, saj se tudi razume, da so pozitivna. Na primer: +1, +2, +3 ... in tako naprej.

-0, v katerem znak ni pomemben, ker ga ne doda, da ga odšteje od neke količine. Toda 0 je zelo pomembna, saj je referenca za cela števila: na eni strani so pozitivni in negativni, kot vidimo na zgornji sliki.

-Negativna cela števila, ki jih je treba vedno zapisati iz znaka -, saj z njimi zneski, kot so dolgovi, in vsi, ki so na drugi strani reference. Primeri negativnih celih števil so: -1, -2, -3 ... in od takrat.

Kako so celotne številke?

Na začetku predstavljamo celotne številke z nastavitvijo nastavitve: z = … -4, -3, -2, -1, 0, +1, +2, +3, +4…, to je, torej naveden in organiziran. Toda zelo uporabna reprezentacija je tisto, kar uporablja numerično linijo. Za to je treba narisati črto, ki je običajno vodoravna, na kateri je 0 označen in razdeljen na enake odseke:

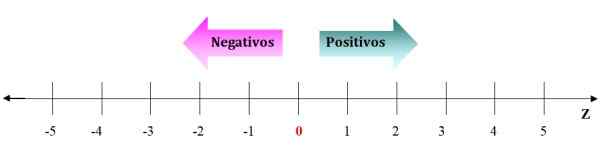Slika 2. Predstavitev celotnih številk na številčni črti. Od 0 na desno so pozitivna cela števila in od 0 na levo negativno. Vir: f. Zapata.

Negativi gredo levo od 0 in pozitivni gredo v desno. Puščice na številčni vrstici simbolizirajo, da številke še naprej do neskončnosti. Glede na katero koli celotno število je vedno mogoče najti tisto, ki je večja ali drugače, kot je nižja.

Absolutna vrednost celoštevilca

Absolutna vrednost celoštevilca je razdalja med številko in 0. In razdalje so vedno pozitivne. Zato je absolutna vrednost negativnega celotnega števila številka brez njegovega znaka manj.

Na primer, absolutna vrednost -5 je 5. Absolutna vrednost je označena z palicami, kot sledi:

| -5 | = 5

Če ga želite vizualizirati, je dovolj, da imamo prostore na številčni črti, od -5 do 0. Medtem ko je absolutna vrednost pozitivnega števila enaka številka, na primer | +3 | = 3, saj je razdalja do 0 3 prostori:

Vam lahko služi: Zakon o sendvič: Pojasnilo in vaje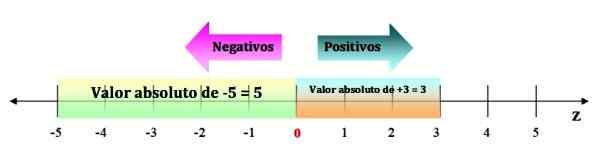Slika 3. Absolutna vrednost celoštevilca je vedno pozitiven znesek. Vir: f. Zapata.

Lastnosti

-Nabor celih števil je označen kot z in vključuje nabor naravnih števil n, njihovi elementi pa so neskončni.

-Celo število in tisto, ki sledi (ali tistega, ki je pred njim) se vedno razlikuje v enoti. Na primer, potem ko 5 pride na 6, je 1 razlika med njimi.

-Vsaka celotna številka ima predhodnika in naslednika.

-Katero koli pozitivno celo število je večje od 0.

-Negativno celo število je vedno manjše od 0 in da je kakršno koli pozitivno število. Vzemimo za primer številko -100, to je manj kot 2, kot 10 in 50. Vendar je tudi manj kot -10, -20 in -99 in je večji od -200.

-0 nima premislekov o znakih, saj ni negativen ali pozitiven.

-S celotnimi številkami je mogoče izvesti iste operacije, ki se izvajajo z naravnimi številkami, in sicer: vsota, odštevanje, množenje, potenciranje in še več.

-Celotno nasprotje določenemu celotnemu X, je -x in vsota celoštevilca z nasprotnim je 0:

x + (-x) = 0.

Operacije s celotnimi številkami

- Dodatek

-Če imajo številke, ki jih je treba dodati enak znak, dodane njihove absolutne vrednosti in rezultat je postavljen znak, ki ga imajo dodatki. Tu je nekaj primerov:

a) (+8) +( +9) = 8 +9 = +17

b) (-12) + ( - 10) = - (12 + 10) = -22

-V primeru, da so številke različnih znakov, se absolutne vrednosti (glavni mladoletni) odštejejo in rezultat je postavljen znak številke z najvišjo absolutno vrednostjo, kot sledi:

a) (-8) + (21) = 21 - 8 = 13

b) (-9) + (+4) = -(9-4) = -5

Lastnosti vsote celih številk

-Vsota je komutativna, zato vrstni red dodatkov ne spremeni vsote. Naj bo A in B dve celotni številki, izpolnjeno je, da je A+B = B+A

-0 je nevtralni element vsote celih števil: a + 0 = a

-Vsaka celotna številka, dodana z nasprotnim, je 0. Nasprotno + a je -a in obratno, nasprotno od -a es + a. Zato: (+ a)+ (-a) = 0.

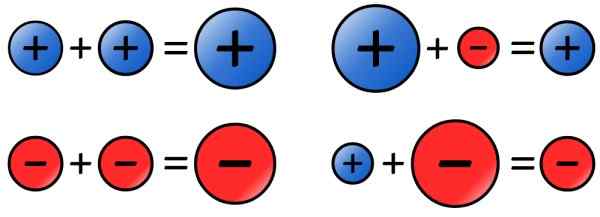Slika 4. Znaki pravijo za vsoto celih številk. Vir: Wikimedia Commons.

- Odštevanje

Če želite odšteti celotne številke, morate to pravilo voditi: Odštevanje je enakovredno vsoti števila s svojim nasprotnim. Pustite dve številki A in B, nato:

A - B = A + (-B)

Recimo, da morate narediti naslednjo operacijo: (-3) - (+7), nato:

(-3) -(+7) = (-3)+( -7) = -(3+7) = -10

- Množenje

Pomnoževanje celotnih številk sledi določenim pravilom za znake:

-Izdelek dveh številk Isti znak Vedno je pozitivno.

-Ko se dve številki pomnožita različni znaki, Rezultat je vedno negativen.

Vam lahko služi: kakšni so deli frakcije? (Primeri)

-Vrednost izdelka je enaka pomnožitvi ustreznih absolutnih vrednosti.

Takoj nekaj primerov, ki pojasnjujejo zgoraj:

(-5) x (+8) = -5 x 8 = -40

(-10) x (-12) = 10 x 12 = 120

(+4) x (+32) = 4 x 32 = 128

Lastnosti množenja celih številk

-Množevanje je komutativno. Biti dve celotni številki A in B, res je, da: a.b = b.a, ki se lahko izraža tudi kot:

Vrstni red dejavnikov ne spremeni izdelka.

-Nevtralni element množenja je 1. Biti celo število.1 = 1

-Katero koli celo število, pomnoženo za 0, je enako 0: a.0 = 0

Distribucijska lastnina

Množevanje ustreza distribucijskim premoženjem glede na vsoto. DA A, B in C sta potem celotna številka:

do.(B +C) = a.b + a.c

Nato primer, kako uporabiti to lastnost:

(-3). [(-4) + 11] = (-3).(-4)+(-3).11 = 12 -33 = 12 + (-33) = -21

Potencial

-Če je osnova pozitivna, je rezultat operacije vedno pozitiven.

-Kadar je osnova negativna, če je eksponent enakomerni, je rezultat pozitiven. In če je eksponent čuden, je rezultat negativen.

- Delitev

V diviziji veljajo enaka pravila znakov kot pri množenju:

-Z delitvijo dveh celih števil istega znaka je rezultat vedno pozitiven.

-Ko sta razdeljena dva cela števila različnih znakov, je količnik negativen.

Na primer:

(-12) ÷ (-4) = 3

33 ÷ (-3) = -11

Pomembno: Delitev ni komutativna, z drugimi besedami do ÷ b ≠ b ÷ a in kot vedno, delitev med 0 ni dovoljena.

- Potencial

Bodite celotna številka in ga želimo dvigniti na eksponent n, potem se moramo pomnožiti sami, kot je prikazano spodaj:

doⁿ = a.do.do.do.… Do

Razmislimo tudi o naslednjem, ob upoštevanju, da je n naravno število:

-Če je a negativen in n enakomerno, je rezultat pozitiven.

-Kadar je a negativen in n čuden, ima za posledico negativno število.

-Če je a pozitiven in n enakomerno ali čuden, je vedno pozitivno celo število.

-Katero koli celo število, dvignjeno na 0, je enako 1: a⁰ = 1

-Vsaka številka visoka do 1 je enaka številu: a¹ = a

Povedamo na primer, ki ga želite najti (-3)⁴ , Da se pomnoži (-3) štirikrat sam, kot je ta: (-3).(-3).(-3).(-3) = 81.

Drug primer, tudi z negativnim številom je:

(-2)³ = (-2).(-2).(-2) = -8

Produkt enakih osnovnih moči

Recimo, da dve moči enake osnove, če jih pomnožimo, dobimo drugo moč z isto osnovo, katere eksponent je vsota danih eksponentov:

doⁿ · Do^m = a^{n + m}

Enako osnovno razmerje v prahu

Z deljenjem moči iste osnove je rezultat moč z isto osnovo, katere eksponent je odštevanje danih eksponentov:

Vam lahko služi: koti v obodu: vrste, lastnosti, rešene vaje

doⁿ ÷ a^m = a^{n - m}

Nato dva primera, ki pojasnjujeta te točke:

(-2)³.(-2)⁵ = (-2) ³⁺⁵= (-2)⁸

5⁶ ÷ 5⁴ = 5^6-4 = 5²

Primeri

Oglejmo si preproste primere, da uporabimo ta pravila, pri čemer ne pozabimo, da je v primeru pozitivnih celih števil, da se znak izpusti:

a) (+6) + (+14) = 6 + 14 = 20

b) (-8) + ( - 10) = - (8 + 10) = -18

c) (-16) + (+7) = -16 + 7 = -9

d) (+4) + (-8) + (-25) = [(+4) + (-8)] + (-25) = [4-8] -25 = -4 -25 = -29

E) (-8) -( + 15) = (-8) + (-15) = -8 -15 = -23

f) (+3) x (+9) = 3 x 9 = 27

g) (- 4) x (-11) = 4 x 11 = 44

H) (+5) x (-12) = -5 x 12 = -60

i) (-2)³ = (-2) x (-2) x (-2) = -8

Rešene vaje

- Vaja 1

Mravlja se premika na številčni črti slike 1. Začenši od točke x = +3 izvede naslednje premike:

-7 enot se premakne v desno

-Zdaj se na levo vrne 5 enot

-Sprehodite se 3 enote na levi strani.

-Vrne in premakne 4 enote v desno.

V katerem trenutku je mrav na koncu poti?

Rešitev

Pokličimo premike. Ko so na desni strani, imajo pozitiven znak in ko so na levem negativnem znaku. Na ta način in začenši od x = +3 imate:

-Prvi D: x₁ = +3 +7 = +10

-Drugi D: x₂ = +10 +(-5) = +5

-Tretji D: x₃ = +5 +(-3) = +2

-Četrti D: x₄ = +2 +4 = +6

Ko se mravlja konča, je sprehod v položaju x = +6. To pomeni, da je 6 enot desno od 0 na številčni črti.

- Vaja 2

Rešite naslednjo operacijo:

36 + [- (-4 + (-5)- 7)].-[-6+5- (2+7-9)]+2 (-8+6)]

Rešitev

Ta operacija vsebuje znake združevanja, ki so oklepaji, kvadratni oklepaji in ključi. Pri reševanju morate najprej skrbeti za oklepaje, po kvadratnih oklepajih in na koncu za tipke. Z drugimi besedami, delati morate od znotraj Out.

V tej vaji točka predstavlja množenje, toda v primeru med eno številko in oklepajem ali drugim simbolom ni smiselno.

Nato ločljivost korak za korakom služijo kot vodnik za sledenje rezultatu zmanjšanja oklepajev, ki so najbolj notranji skupinski simboli:

36 + [- (-4 + (-5)- 7)].-[-6+5- (2+7-9)]+2 (-8+6)] =

= 36 + [- (-16)].-[-6+ 5- (0)]+ 2 (-2)] =

= 36 + [16].-[-1] -4] =

= 52.1- 4] = 52.-3 = -156

- Vaja 3

Rešite enačbo prve stopnje:

12 + x = 30 + 3x

Rešitev

Izrazi so združeni z neznano levo od enakosti in številčnimi izrazi na desni:

x - 3x = 30 - 12

- 2x = 18

X = 18 / (-2)

x = - 9