Dvojno vzorčenje

Pojasnjujemo, kaj je dvojno vzorčenje, primere, prednosti in slabosti, in damo rešene vaje

Pri dvojnem vzorčenju želite bolj globoko vedeti spremenljivko populacije

Kaj je dvojno vzorčenje?

On Dvojno vzorčenje Gre za tehniko, ki se uporablja v inferencialni statistiki, ko želite vedeti več podrobnosti in gotovosti o določeni spremenljivki, ki je značilna za določeno populacijo.

Drugi populacijski vzorec se običajno izvede po prvem vzorcu, katerega analiza ni pokazala statistično pomembnega zaključka o kateri koli od spremenljivk študije, ki je bila sprejeta in analizirana.

Zaradi tega je znano tudi vzorčenje dvojnih statistik kot Dve fazi vzorčenja. Uporabnost drugega vzorca je, v katerem pomaga natančneje določiti oceno razlogov in regresij določene pomožne spremenljivke, ki nastanejo v luči analize prvega vzorca.

Druga uporaba, ki je dana dvojnemu vzorčenju, je zbiranje informacij za uresničitev vzorčenja slojev.

Primeri

Spodaj so različne situacije, v katerih je dvojno vzorčenje upravičeno.

Nadzor kakovosti v izdelavi kosov

Metoda dvojnega vzorčenja se pogosto uporablja pri nadzoru industrijske kakovosti in se običajno izvaja v dveh fazah.

Recimo na primer industrijski stroj, ki pripravi določene kose. Kolikor je stroj prilagojen, noben kos ni enak drugemu, saj lahko v njegovih dimenzijah in teži majhne razlike. Gre za ugotovitev, ali veliko delov, ki jih izdeluje omenjeni stroj.

Najprej je vzet naključni vzorec kosov, s katerimi je treba preveriti eno od spremenljivk, na primer dolžina kosa je znotraj tolerance.

V primeru, da je povprečna dolžina pod ali nad želeno stopnjo tolerance do omenjene spremenljivke, v tem prvem vzorcu je sklepano, da je parcela pokvarjena in jo je treba zavreči. V tem primeru ni treba jemati novih vzorcev.

Vam lahko služi: koeficient korelacije: formule, izračun, razlaga, primer

Nasprotno, če je povprečna vrednost v območju tolerance, vendar je standardni odklon vzorca dovolj velik, da je vsota ali odštevanje povprečne vrednosti zunaj roba, potem bo treba zbrati drugi večji vzorec.

Ta drugi vzorec mora vključevati prvotni vzorec, da ponovno preoblikuje izračune in s tem lahko končno odločimo o preiskani spremenljivki. Na ta način je mogoče vedeti, če je parcela pokvarjena ali ne.

Zmanjšanje stroškov vzorčenja

Večkrat je težko dostopati do informacij o eni od spremenljivk, do katerih želite preučiti. Toda za zbiranje podatkov lahko lažje obstaja pomožna spremenljivka.

V tem primeru sta odvzeta dva vzorca, velik za pomožno spremenljivko, manj drag in manjši vzorec, ki ga vsebuje glavni vzorec najdražje spremenljivke.

Ta metoda je uporabna vsakič, ko se ugotovi, da obstaja povezava med obema spremenljivkama, kar je na splošno razmerje sorazmernosti.

Primer te situacije se pojavlja v gozdnih vedah, kjer je zaželeno določiti odstotek dreves, ki jih je prizadela zajedavska rastlina (La Tiña).

Ker so te zelo obsežne in težko dostopne regije, je celotno populacijo dreves v času in stroškov neizvedljivo. Tem korakom se nato sledi:

1. korak: Vzorčenje

Predhodno vzorčenje bi bilo sestavljeno iz uporabe zračne fotografije, gozd pa je razdeljen na sklope. Z analizo slik izbranih sklopov je izbranih nekaj sklopov naključno in ocenjeno, koliko dreves vpliva na barvo dreves.

Vam lahko služi: euclid teorem

2. korak: Terensko delo

Toda fotografska analiza ne more biti natančna, zato nadaljujemo z izbiro, po možnosti naključno, nekaj veliko prvega vzorca, ki opravi terensko delo.

3. korak: Primerjava

Potem rezultat polja primerjamo s fotografijo za prestrezanje dveh sklopov. Ta primerjava je mogoče izvesti na primer, tako da je graf, v katerem je vodoravna os vrednosti, ki jo za vsako serijo dobimo s fotografijo in na navpični osi vrednost, ki jo dobimo s sklopom s terenskim delom.

Ta grafična metoda omogoča vizualno ugotavljanje, ali obstaja povezava med obema rezultatima ali ne, in z regresijsko analizo določimo koeficient sorazmernosti ali razmerja med obema vzorcima.

Po glavnem vzorcu, to je fotografski vzorec, se vzame povprečna vrednost okuženih dreves in njegov standardni odklon. Ker pa sta bila določena koeficient proporcionalnosti in njegova napaka z vzorci polja, je mogoče popraviti rezultat glavnega vzorca (fotografija).

Potem lahko ta rezultat ekstrapoliramo na popolno populacijo dreves.

Prednosti in slabosti dvojnega vzorčenja

V opisanih primerih je stroškovno prednost dokaz.

Slabost je, da v primeru dvojnega vzorčenja za nadzor kakovosti obstaja tveganje, da bo šel skozi dobro veliko izdelkov, ki so iz tolerance.

Vaja

Želite oceniti število bolnih dreves v gozdu 162 hektarjev. Ker je gozd zelo obsežen, je razdeljen na 100 parcel istega območja. 18 parcel je izbranih naključno in s fotografsko študijo ocenjujejo, da je na teh 18 parcelah 8 bolnih dreves s standardno napako približno 4,5 dreves.

Vam lahko služi: kakšni so deli frakcije? (Primeri)

Od teh 18 ploskv je 8 ploskv izbranih naključno. Za te osmih zapletov fotografska študija povzroči 10 bolnih dreves z napako več ali manj 5,3 dreves.

Po drugi strani pa za istih osem parcel terenska študija vrže 12,4 bolnih dreves z napako več kot 6,3 dreves.

Zahteva se:

• a) Določite koeficient sorazmernosti med terensko študijo z linearno regresijo.
• b) Ocenite število bolnih dreves s pomočjo fotografske metode na stotih parcelah.
• c) Za oceno realnega števila bolnih dreves v celotnem gozdu uporabite popravek s koeficientom proporcionalnosti.

Rešitev

Graf števila dreves na fotografsko število v primerjavi s poljem za osem sklopov, izbranih za obe študiji.

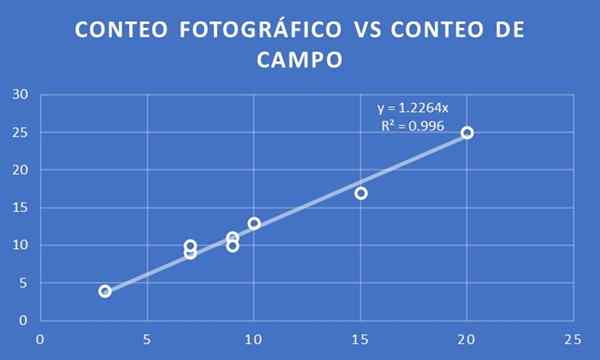Fotografsko štetje v primerjavi s številom polja. Vir: f. Zapata.

Trend linija je prilagojena in določena je njegov naklon. V tem primeru je pridobljeno, da je koeficient proporcionalnosti 1,23. To pomeni, da če je X številka fotografskega štetja, se nato oceni, da bo število polja y = 1,23 x.

Število bolnih dreves glede na fotografsko štetje v 18 izbranih sklopih bo:

18 x 8,5 = 153

Ker pa je bil celoten gozd razdeljen na 100 parcel istega območja, je število bolnih dreves, ocenjenih s fotografsko metodo,: (100/18) x 153 = 850.

Zdaj je uporabljen korekcijski faktor, dobljen s primerjavo med terensko in fotografsko študijo:

Ocenjeno resnično število bolnih dreves v gozdu = 1,23 x 850 = 1046.

Reference

1. Dvojni vzorec za oceno razmerja, Pennstate College. Pridobljeno iz PSU.Edu
2. Dvojna, večkratna in segencijska vzorca, NC State University. Okreval od NCSU.Edu
3. Preprosto naključno vzorčenje. Okrevano iz Investopedije.com
4. Kaj je dvojno vzorčenje? Okreval od: NIST.Gov
5. Vzorec. Pridobljeno iz: v.Wikipedija.org
6. Večstopenjski vzorec. Pridobljeno iz: v.Wikipedija.org