Akumulirana frekvenčna formula, izračun, porazdelitev, primeri

The nakopičena frekvenca To je vsota absolutnih frekvenc F, od otroka, do katere ustreza določeni vrednosti spremenljivke. Po drugi strani je absolutna frekvenca, kolikokrat se v naboru podatkov prikaže opazovanje.

Očitno mora biti spremenljivka študije urejena. In ker se nakopičena frekvenca dobi z dodajanjem absolutnih frekvenc, se izkaže, da mora nakopičena frekvenca do zadnjega podatkov sovpadati s skupnim številom le -teh. V nasprotnem primeru je pri izračunih napaka.

Nakopičena frekvenca se uporablja pri upravljanju statističnih podatkov

Na splošno je nakopičena frekvenca označena kot F_Yo (Ali včasih n_Yo), da ga ločimo od absolutne frekvence F_Yo in pomembno je dodati stolpec zanj v tabelo, s katero so podatki organizirani, znani kot Tabela frekvence.

Na ta način je med drugim olajšati, da se upošteva, koliko podatkov je bilo prešteti do določenega opazovanja.

A f_Yo Znan je tudi kot Absolutno nakopičena frekvenca. Če razdelite med skupne podatke, imate Relativna nakopičena frekvenca, katere končna vsota mora biti enaka 1.

[TOC]

Formule

Nakopičena frekvenca določene vrednosti spremenljivke x_Yo  To je vsota absolutnih frekvenc F vseh vrednosti, nižjih ali enakih:

F_Yo  = f₁ + F₂ + F₃  +… F_Yo

Z dodajanjem vseh absolutnih frekvenc dobimo skupno število podatkov n, to je:

F₁ + F₂ + F₃ +.. . + F_n = N

Prejšnja operacija na povzetek zapiše simbol vsote ∑:

∑ f_Yo = N

Druge nakopičene frekvence

Nakopičimo lahko tudi naslednje frekvence:

-Relativna frekvenca: Dobimo ga z delitvijo absolutne frekvence F_Yo Med skupnimi podatki n:

F_r = f_Yo / N

Če so relativne frekvence dodane od otroka do tistega, ki ustreza določenemu opazovanju, nakopičena relativna frekvenca. Zadnja vrednost mora biti enaka 1.

-Akumuliran odstotek frekvence: Nakopičena relativna frekvenca na 100% se pomnoži.

F_% = (f_Yo / N) x 100%

Te frekvence so koristne za opis vedenja podatkov, na primer z iskanjem ukrepov osrednje težnje.

Kako dobiti nakopičeno frekvenco?

Za pridobitev nakopičene frekvence je treba naročiti podatke in jih organizirati v tabeli frekvence. Postopek je prikazan v naslednjih praktičnih razmerah:

Vam lahko služi: sestavljeno nasledstvo

-V spletni trgovini, ki prodaja mobilne telefone, prodajni zapis določene blagovne znamke meseca marca, naslednje vrednosti na dan:

1; 2; 1; 3; 0; 1; 0; 2; 4; 2; 1; 0; 3; 3; 0; 1; 2; 4; 1; 2; 3; 2; 3; 1; 2; 4; 2; 1; 5; 5; 3

Spremenljivka je Število telefonov, prodanih na dan In je kvantitativno. Predstavljenih podatkov ni tako enostavno razlagati, na primer lastniki trgovine bi lahko zanimali, ali obstaja kakšen trend, na primer dnevi v tednu, ko so prodaja te blagovne znamke večja, so večja.

Informacije, kot je ta in še več, lahko dobite tako, da podatke predložimo na urejen način in določite frekvence.

Kako zapolniti tabelo frekvence

Za izračun nakopičene frekvence se podatki naročijo:

 0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 2; 2; 2; 2; 3; 3; 3; 3; 3; 3; 4; 4; 4; 5; 5

Nato je zgrajena tabela z naslednjimi informacijami:

-Prvi stolpec na levi s količino prodanih telefonov, med 0 in 5 in v naraščajočem vrstnem redu.

-Drugi stolpec: absolutna frekvenca, ki je število dni, ki so bili prodani 0 telefonov, 1 telefona, 2 telefonov in tako naprej.

-Tretji stolpec: nakopičena frekvenca, sestavljena iz vsote prejšnje frekvence in frekvence podatkov, ki jih je treba upoštevati.

Ta stolpec se začne s prvim stolpcem stolpca absolutne frekvence, v tem primeru je 0. Za naslednjo vrednost je to dodano s prejšnjo. Tako se nadaljujejo zadnji podatki nakopičene frekvence, ki morajo sovpadati s skupnimi podatki.

Tabela modnosti

Naslednja tabela prikazuje spremenljivka "Število telefonov, ki se prodajajo v enem dnevu", njena absolutna frekvenca in podroben izračun njene nakopičene frekvence.

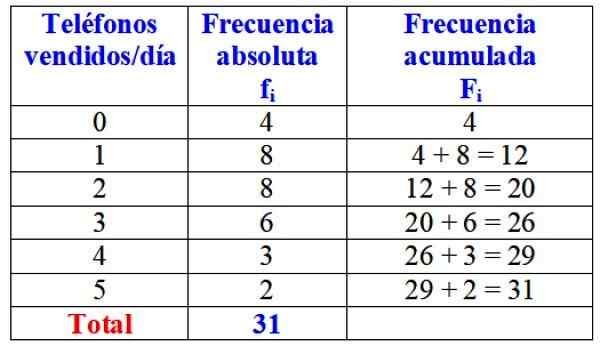Tabela absolutnih in nakopičenih frekvenc za spremenljivko "telefoni, ki se prodajajo na dan". Vir: f. Zapata.

Na prvi pogled bi lahko rekli, da se zadevna blagovna znamka skoraj vedno prodaja na enem ali dveh telefonih na dan, saj je najbolj absolutna frekvenca 8 dni, kar ustreza tem vrednostim spremenljivke. Samo 4 dni v mesecu ni prodal niti enega telefona.

Lahko vam služi: trigonometrični razlogi: primeri, vaje in aplikacije

Kot je navedeno, je lažje preučiti tabelo kot prvotno zbrani podatki.

Nakopičena frekvenčna porazdelitev

Nakopičena frekvenčna porazdelitev je tabela, v kateri so na voljo absolutne frekvence, nakopičene frekvence, nakopičene relativne frekvence in nakopičene odstotne frekvence.

Medtem ko je prednost organiziranja podatkov v tabeli, kot je prejšnja, če je številka podatkov zelo velika, je možno, da jih ni dovolj organizirati, kot je prikazano zgoraj, ker če se pojavijo številne frekvence, je še vedno težko razlagati.

Težavo je mogoče odpraviti z gradnjo a Porazdelitev frekvence Po presledkih uporaben postopek, kadar spremenljivka vzame veliko število vrednosti ali če gre za neprekinjeno spremenljivko.

Tu so vrednosti razvrščene v intervale enake amplitude, imenovane razred. Za razrede je značilno, da imajo:

-Omejitev razreda: so ekstremne vrednosti vsakega intervala, dve, zgornja meja in spodnja meja. Na splošno zgornja meja ne pripada intervalu, ampak v neposredni naslednji, medtem ko spodnja meja spada.

-Blagovna znamka razreda: Je sredi točke vsakega intervala in je jemana kot reprezentativna vrednost.

-Širina razreda: Izračuna se tako, da odštejemo vrednost glavnega in najmanjšega (razpon) in deli po številu razredov:

Širina razreda = obseg / število razredov

Potem je podrobno opisana izdelava frekvenčne porazdelitve.

Primer

Ta nabor podatkov ustreza 40 ocenah izpita za matematiko na lestvici od 0 do 10:

0; 0; 0; 1; 1; 1; 1; 2; 2; 2; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 9; 9; 10; 10.

Razviti je mogoče frekvenčno porazdelitev z določeno količino razredov, na primer 5 razredov. Upoštevati je treba, da pri uporabi številnih razredov podatkov ni enostavno razlagati in občutek izvajanja skupine je izgubljen.

Vam lahko služi: koliko morate dodati 3/4, da dobite 6/7?

In če so nasprotno razvrščeni v zelo malo, potem so informacije razredčene in del tega se izgubi. Vse je odvisno od količine podatkov, ki jih imate.

V tem primeru je dobro imeti dva ocena v vsakem intervalu, saj je 10 rezultatov in 5 razredov bo. Ranka je odštevanje med glavno in najmanjšo oceno, širina razreda:

Širina razreda = (10-0)/5 = 2

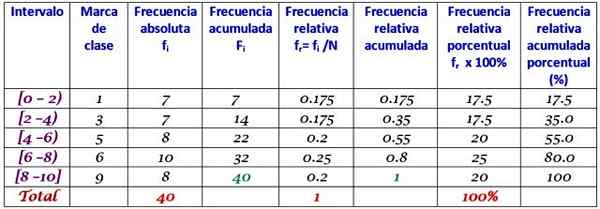
Intervali so zaprti z levo in odprti na desni (razen zadnjega), ki je simbolizirana s kvadratnimi oklepaji in oklepaji. Vsi imajo enako širino, vendar ni obvezna, čeprav najpogostejša.

Vsak interval vsebuje določeno količino elementov ali absolutne frekvence, v naslednjem stolpcu. Tabela prikazuje tudi relativno frekvenco F_r  (absolutna frekvenca med skupnim številom podatkov) in odstotkom odstotka f frekvence F_r × 100%.

Predlagana vaja

Podjetje je v prvih dveh mesecih v letu vsakodnevno klicalo svojim strankam. Podatki so naslednji:

6, 12, 7, 15, 13, 18, 20, 25, 12, 10, 8, 13, 15, 6, 9, 20, 24, 12, 7, 10, 11, 13, 9, 12, 15, 15, 15, 15, 18, 20, 13, 17, 23, 25, 14, 18, 6, 14, 16, 9, 6, 10, 12, 13, 17, 14, 26, 7, 7, 12, 2, 7, 7

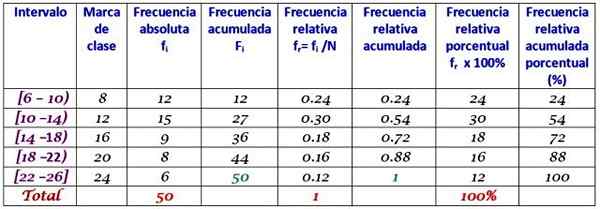
Skupino v 5 razredih in gradite tabelo s frekvenčno porazdelitvijo.

Odgovor

Širina razreda je:

(26-6)/5 = 4

Poskusite rešiti, preden vidite odgovor.

Reference

1. Berenson, m. 1985. Statistični podatki za upravo in ekonomijo. Interameriški s.Do.
2. Devore, j. 2012. Verjetnost in statistika za inženirstvo in znanost. 8. Izdaja. Cengage.
3. Levin, r. 1988. Statistika za skrbnike. 2. mesto. Izdaja. Dvorana Prentice.
4. Verjetnost in statistika. Širina intervala razreda. Pridobljeno iz: Pedroprobabilnost in stadistično.Blogspot.com.
5. Spiegel, m. 2009. Statistika. Serija Schaum. 4 ta. Izdaja. McGraw Hill.
6. Walpole, r. 2007. Verjetnost in statistika za inženirstvo in znanost. Pearson.