Položajski ukrepi, osrednja težnja in disperzija

The Ukrepi osrednje, disperzijske in položaja, To so vrednosti, ki se uporabljajo za pravilno razlago nabora statističnih podatkov. Te lahko delamo neposredno, kot je pridobljeno iz statistične študije, ali pa jih je mogoče organizirati v skupinah enake frekvence, kar olajša analizo.

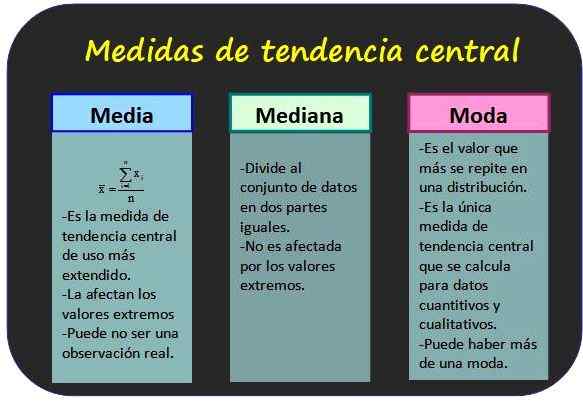
Trije najbolj znani centralni trendni ukrepi in nekatere njegove lastnosti. Vir: f. Zapata.

Ukrepi osrednje težnje

Omogočajo vedeti, katere vrednosti so statistični podatki združeni.

Aritmetično povprečje

Znano je tudi kot povprečje vrednosti spremenljivke in ga dobimo z dodajanjem vseh vrednosti in delitvijo rezultata s skupnim številom podatkov.

• Aritmetična srednja za podatke brez združevanja

Bodite spremenljivka x, ki je ni podatkov brez organiziranja ali združevanja, njegova aritmetična srednja vrednost se izračuna na naslednji način:

In povzetek zapisa:

Primer

Lastniki gorskega turističnega hostla nameravajo vedeti, koliko dni v povprečju ostanejo v objektih. Za to je bil izveden zapis o stalnosti 20 skupin turistov in pridobil naslednje podatke:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

Povprečni dnevi, v katerih ostanejo turisti, so:

= 2.5 dni

• Aritmetična srednja za združene podatke

Če so spremenljivi podatki organizirani v absolutni frekvenčni tabeli F_Yo In razredni centri so x₁, x₂,…, X_n, Povprečje se izračuna z:

V povzetku poletja:

Mediana

Mediana skupine N vrednosti spremenljivke x je osrednja vrednost skupine, pod pogojem, da so vrednosti vse pogosteje urejene. Na ta način je polovica vseh vrednosti nižja od mode, druga polovica.

• Medij ne -združenih podatkov

Predstavimo lahko naslednje primere:

-Število n Vrednosti spremenljivke x  Čuden: Mediana je vrednost, ki je ravno na sredini skupine vrednosti:

-Število n Vrednosti spremenljivke x par: V tem primeru se mediana izračuna kot povprečje dveh osrednjih vrednosti podatkovne skupine:

Primer

Če želite najti mediano podatkov o turističnem hostlu, jih najprej naročijo od najmanj do največjih:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Lahko vam služi: kakšna je relativna frekvenca in kako se izračuna?

Številka podatkov je enakomerna, zato obstajata dva osrednja podatkov: x₁₀ in x_enajst In ker sta oba vredna 2, tudi njegovo povprečje.

Mediana = 2

• Medij združenih podatkov

Uporablja se naslednja formula:

Simboli v formuli pomenijo:

-C: interval širina, ki vsebuje mediano

-B_M: spodnja meja istega intervala

-F_m: Število opazovanj, ki vsebujejo interval, v katerega pripada mediana.

-N: Skupni podatki.

-F_Bm: Število opazovanj pred intervalom, ki vsebuje mediano.

Moda

Moda za ne -združene podatke je najpogostejša vrednost, za združene podatke pa je to najpogostejši razred. Modno velja za najbolj reprezentativne podatke ali razred distribucije.

Dve pomembni značilnosti tega ukrepa je, da ima nabor podatkov več kot eno modo, modo pa je mogoče določiti tako za kvantitativne podatke kot za kvalitativne podatke.

Primer

Nadaljevanje s podatki turističnega hostla je tisto, ki se najbolj ponavlja, 1, zato je najbolj običajno, da turisti ostanejo 1 dan v hostlu.

Ukrepi disperzije

Disperzijski ukrepi opisujejo, kako so razvrščeni podatki okoli osrednjih ukrepov.

Domet

Izračuna se z odštevanjem glavnih podatkov in manjših podatkov. Če je ta razlika velika, je znak, da se podatki razpršijo, majhne vrednosti pa kažejo, da so podatki blizu povprečju.

Primer

Obseg podatkov o turističnem hostlu je:

Razpon = 5–1 = 4

Odstopanje

• Varianta za ne -združene podatke

Najti varianco s² Najprej je treba najprej vedeti aritmetično povprečje, nato pa se razlika izračuna na kvadrat med vsakim podatkom in povprečjem, vse pa se dodajo in delijo s skupnimi opazovanji. Te razlike so znane kot odstopanja.

Varianta, ki je vedno pozitivna (ali nič), kaže, kako daleč so opazovanja povprečja: če je varianca visoka, so vrednosti bolj razpršene kot kadar je varianta majhna.

Primer

Varianta za podatke turističnega hostla je:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

= 1.95

• Odstopanje za združene podatke

Za iskanje variance skupine združenih podatkov so potrebne: i) povprečje, ii) frekvenca f_Yo  ki so skupni podatki v vsakem razredu in iii) x_Yo  ali vrednost razreda:

Lahko vam služi: vrste trikotnikov

Standardni odklon

Standardni odklon je pozitiven kvadratni koren variance, tako da ima prednost pred odstopanjem: na voljo je v enakih enotah kot spremenljivka, ki je v študiji, in tako ima bolj neposredno idejo kot tesno ali daleč, ki je spremenljivka povprečnega.

• Standardni odklon za ne -združene podatke

Določen je preprosto tako, da najdete kvadratni koren variance za porušene podatke:

 Primer

Standardni odklon za podatke o turističnem hostlu je:

S = √ (s²) = √1.95 = 1.40

• Standardni odklon za združene podatke

Izračuna se z iskanjem kvadratnega korena variance za združene podatke:

Pozicijski ukrepi

Ukrepi za položaj razdelijo urejen niz podatkov na enake dele. Srednja mediana je poleg osrednjega ukrepanja tudi merilo položaja, saj celoto deli na dva enaka dela. Lahko pa dobite manjše dele s kvartili, decili in odstotki.

Kvartile

Quartiles razdelimo na štiri enake dele, vsak s 25 % podatkov. Označeni so kot Q₁, Q₂ in q₃ In mediana je četrti Q₂. Na ta način je 25% podatkov pod četrtino Q₁, 50% pod četrtino Q₂ ali mediana in 75% pod četrtino q₃.

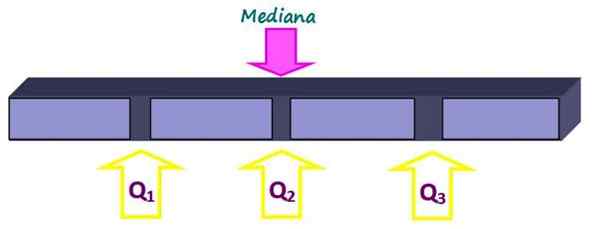Slika 2. Kvartili razdelijo nabor podatkov na štiri enake dele. Vir: f. Zapata.

• Kvartile za neokrožene podatke

Podatki so naročeni in skupno razdeljeno v 4 skupine z enakim številom podatkov. Položaj prvega kvartila najdemo z:

Q₁ = (n+1)/4

Skupni podatki. Če so rezultat celotni podatki, ki ustrezajo temu položaju, če pa je decimalna, so podatki, ki ustrezajo celotnemu delu z naslednjim.

Primer

Položaj prvega kvartila Q₁ Za podatke turističnega hostela so:

Q₁ = (n+1) / 4 = (20+1) / 4 = 5.25

To je položaj kvartila 1 in ker je rezultat decimalno, se podatki X iščejo₅ in x_6, ki so x₅ = 1 in x₆ = 1 in so v povprečju, kar ima za posledico:

Prvi kvartil = 1

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Položaj drugega kvartila Q₂ je:

Vam lahko služi: teleskopska vsota: kako je rešena in rešena vaje

Q₂ = 2 (n+1)/4 = 10.5

Kar je povprečje med x₁₀ in x_enajst in sovpada z mediano:

Drugi kvartil = mediana = 2

Tretji kvartilni položaj se izračuna z:

Q₃ = 3 (n+1) / 4 = 3 (20+1) / 4 = 15.75

Je tudi decimalna, zato je x povprečno_petnajst in x₁₆:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Toda kot sta oba vredna 4:

Tretji kvartil = 4

Splošna formula za položaj kvartilov v zadostnih podatkih je:

Q_k = K (n+1)/4

S k = 1,2,3.

• Kvartile za združene podatke

Izračunani so podobno kot mediana:

Pojasnilo simbolov je:

-B_Q: spodnja meja intervala, ki vsebuje kvartil

-C: Širina tega intervala

-F_q: Število opazovanj je vsebovalo kvartilni interval.

-N: Skupni podatki.

-F_BQ: Število podatkov pred intervalom, ki vsebuje kvartil.

Decili in odstotek

Decili in odstotki razdelijo nabor podatkov na 10 enakih delov oziroma 100 enakih delov, njihov izračun.

• Decili in odstotek za ne -združene podatke

Formule se uporabljajo:

D_k = K (n+1)/10

S k = 1,2,3… 9.

Decile d₅ Mora biti enak mediani.

Str_k = K (n+1)/100

S k = 1,2,3… 99.

Odstotek p_petdeset Mora biti enak mediani.

Primer

V primeru turističnega hostla je položaj D₃ je:

D₃ = 3 (20+1)/10 = 6.3

Kako je v povprečju decimalna številka x₆ in x_7, oba enaka 1:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Pomeni, da je 3 desetine podatkov pod x₇ = 1 in preostali zgoraj.

• Decili in odstotek za združene podatke

Formule so analogne kvartilom. D se uporablja za označevanje decil in P za odstotke, simboli pa se razlagajo na podoben način:

Empirično pravilo

Ko se podatki simetrično porazdelijo in je porazdelitev unimodalna, se imenuje pravilo  Empirično pravilo tudi Pravilo 68 - 95 - 99, ki jih združujejo v naslednjih intervalih:

• 68% podatkov je v intervalu:

• 95% podatkov je v intervalu:

• 99% podatkov je v intervalu:

Primer

V kakšnem intervalu je 95% podatkov o turističnem hostlu?

So v intervalu: [2.5−1.40; 2.5+1.40] = [1.1; 3.9.

Reference

1. Berenson, m. 1985. Statistični podatki za upravo in ekonomijo. Interameriški s.Do.
2. Devore, j. 2012. Verjetnost in statistika za inženirstvo in znanost. 8. Izdaja. Cengage.
3. Levin, r. 1988. Statistika za skrbnike. 2. mesto. Izdaja. Dvorana Prentice.
4. Spiegel, m. 2009. Statistika. Serija Schaum. 4 ta. Izdaja. McGraw Hill.
5. Walpole, r. 2007. Verjetnost in statistika za inženirstvo in znanost. Pearson.