Matematika

Vektorske funkcije

Kaj so vektorske funkcije?

A vektorska funkcija parametra t, Je funkcija, katere domena so resnične vrednosti t, Medtem ko pot tvorijo vektorji oblike r (t). Takšna funkcija je mogoče izraziti kot:

r (t) = f (t) Yo + g (t) J + H (t) k

Kje Yo, J in k So enotni vektorji v treh glavnih smereh prostora, funkcije F, G in H pa so resnične funkcije spremenljivke t. Zapis uporablja krepko, za razlikovanje vektorskih velikosti.

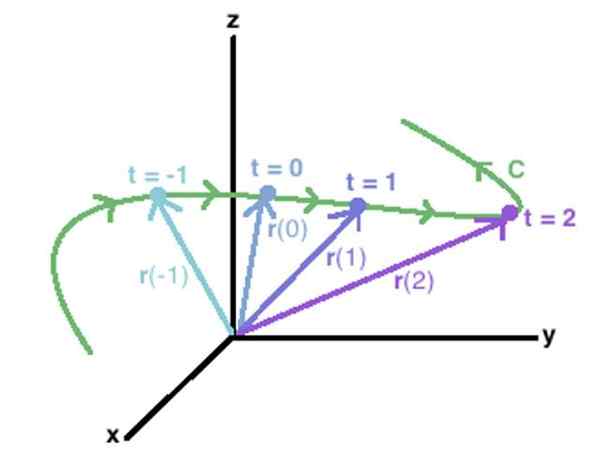Vektorsko funkcijo v prostoru lahko uporabimo za opis krivulje C, pri čemer se pridruži skrajnim točkam vsakega od vektorjev, ki jih določa omenjena funkcija. Vir: Wikidot.

Drug način označevanja vektorske funkcije je s kvadratnimi oklepaji:

r (t) = t), G (t), H (t)>

Vektorske funkcije se lahko uporabijo za preučevanje krivulj v ravnini in prostoru, kot je usmeritev, ki sledi premikajočemu se predmetu. Primer je prispodoba, ki jo opisuje projicirana kroglica z začetno hitrostjo, pod gravitacijo.

Če želite v vsakem trenutku vedeti položaj žoge t, Vektorska funkcija z dvema komponentama, eno vodoravno in eno navpično:

r (t) = x (t) Yo + in (int) J

Oba x (t) kot y (t) So časovne funkcije t. Tako se pri pridružitvi skrajnim točkam vsakega od vektorjev r(t) Možno, oblikujte prispodobo, ki jo je opisala žoga v ravnini Xy.

Koncept se zlahka razširi na C krivuljo v prostoru, kot je tisti, prikazan na zgornji sliki. V njem se pojavljajo vektorji r (-1), r (0), r (1) r (2), katerih konci narišejo c krivuljo, narisano v zeleni.

Omejitve, izpeljane in integral vektorskih funkcij

Orodja za izračun, ki veljajo za resnične spremenljive funkcije, se lahko uporabijo tudi za vektorske funkcije.

Vam lahko služi: faktorizacija

Meja vektorske funkcije

Meja vektorske funkcije r (t) = f (t) Yo + g (t) J + H (t) k, Ko je t → a, je opredeljen kot:

$\dpi110 \displaystyle \lim_t \to a\textbfr(t)=\left [ \displaystyle \lim_ t\to a f(t)\right ]\textbfi+\left [ \displaystyle \lim_ t\to a g(t)\right ]\textbfj+\left [ \displaystyle \lim_ t\to a h(t)\right ]\textbfk$

Ob predpostavki, da obstajajo ustrezne meje F (t), G (t) in h (t), kdaj t → a.

Izhaja iz vektorske funkcije

Opredelitev izhaja iz vektorske funkcije r (t) = f (t) Yo + g (t) J + H (t) k Je analogen derivatu resnične funkcije resnične spremenljivke. Klicati r'(t) Če želite omeniti izpeljan, imate:

$\dpi110 \mathbfr'(t)=\displaystyle \lim_\Delta t \to 0\frac\mathbfr(t+\Delta t)-\mathbfr(t)\Delta t$

Derivat obstaja, kadar obstaja prejšnja meja, in če je tako, funkcija r(t) je različna v t.

Integral vektorske funkcije

Biti r (t) = f (t) Yo + g (t) J + H (t) k vektorska funkcija, tako da so funkcije f, g in h integrirane v t.

Tako:

$\dpi110 \int \mathbfr(t)dt =\left [ \int f(t)dt \right ]\mathbfi+\left [ \int g(t)dt \right ]\mathbfj+\left [ \int h(t)dt \right ]\mathbfk+\mathbfC$

C = c₁Yo + c₂J

Kar pomeni, da je konstanta integracije tudi vektor, vendar konstantna.

Primeri vektorske funkcije

Primer 1

Imate vektorsko funkcijo r (t) = 3sec t Yo + 2Tan t J. Oceniti ga je mogoče za različne t vrednosti, na primer t = π/4 in t = π, kar povzroča vektorje r (π/4) in r (π):

r (π/4) = 3Sec (π/4) Yo + 2TAN (π/4) J = 3√2 Yo + 2 J

r (π) = 3Sec (π) Yo+2Tan (π) J = - 3 Yo

Vendar, r (t) Ne obstaja za vrednosti t = ∓π/2, ∓3π/2, ∓5π/2…, ker funkcija SEC t = 1 /cos t Ni definirano, ali je tako t = sen t / cos t.

Zato so domena funkcije R (t) vse resnične vrednosti T, razen vrednosti oblike:

∓ (2n+1) π/2; Z n = 0, 1, 2, .. .

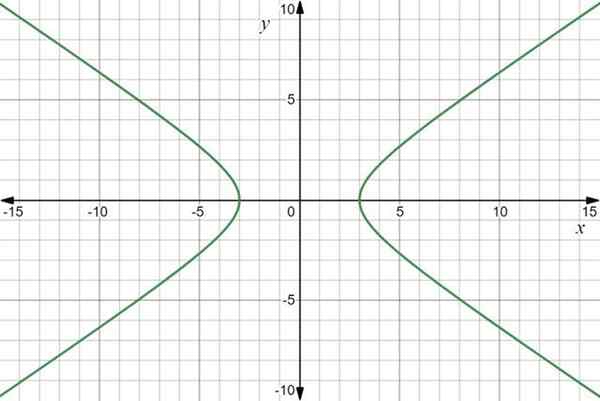
Graf funkcije je hiperbola:

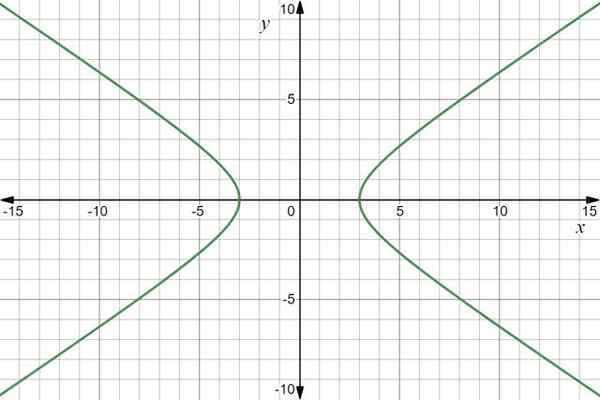Graf vektorske funkcije r (t) = 3sec t Yo+2 porjavelo t J. Vir: f. Zapata skozi Desmos.

Primer 2

Pri nagnjenem izstrelitvi je mobilni položaj vektorska funkcija r (t) = x (t) Yo + in (int) J . Ob predpostavki, da zračna odpornost ne posreduje in da je gravitacija edina sila, ki deluje na mobilnem telefonu, je vodoravno gibanje enakomerno rektno, medtem ko je navpična enakomerno pospešena, saj je g = 9.8 m/s² Vrednost pospeška. Ta pospešek je navpičen proti tlem.

Vam lahko služi: pravila izpeljave (s primeri)

V tem primeru funkcije x (t) in (t) Oni so:

x (t) = x_tudi + v_vol∙ t
in (t) = y_tudi + v_Oy∙ T - ½ gt²

Zneske v_vol in v_Oy So komponente vektorske funkcije, ki ves čas opisujejo mobilno hitrost:

v (t) = v_x(t) Yo + v_in(t) J

v_vol = v_tudi∙ cos θ
v_Oy = v_tudi∙ Sen θ

Kot θ kot, ki tvori začetno hitrost glede na vodoravno.

Začetni položaj mobilnega dela je koordinatna točka (x_tudi,in_tudi) ali enakovredno položaj, ki ga daje:

r_tudi (t) = x_tudi Yo + in_tudi J

Upoštevajte, da je bil v prikazanih enačbah navpični smeri dodeljen negativni znak, zato ga prevzame tretji izraz enačbe za y (t). Prav tako je mogoče dodeliti izvor začetnemu položaju mobilnega telefona.

Takojšnja hitrost izstrelka

Trenutna hitrost V (t) je prvi izhaja iz položaja, glede na čas. Izračuna se z uporabo znanih pravil izpeljave:

v(t) = R ' (t) = [x (t) Yo + in (int) J]'= x '(t) Yo + in '(t) J = v_volYo + (v_Oy - Gt) J

Modul za hitrost je podan z:

$\dpi110 \left|\textbfv \right|=\sqrtv_ox^2+v_oy^2$

Takojšen pospešek projektila

Znano je, da je g, v navpični smeri in smeri navzdol. To je preverjeno, če vemo, da je pospešek prvi izpeljan hitrosti glede na čas (ali drugi derivat položaja glede na čas, če je prednostno):

do(t) = V ' (t) = [V_volYo + (v_Oy - Gt) J] '= [V_volYo] '+ [(v_Oy - Gt) J] '= - g J

To je ravno pričakovani rezultat.

Vaja rešena

Glede na vektorsko funkcijo r (t) = 3T Yo + (T - 1) J, najti R '(t) in r "(T).

Rešitev

Z uporabo pravil o izpeljavi za vsako komponento imate:

Vam lahko služi: integracija konstanta: pomen, izračun in primeri

R '(t) = = 3 Yo + J

In ker je derivat konstante 0:

r "(t) = 0

To pomeni, r "(t) je enak ničelnemu vektorju.

Reference

Figueroa, d. 2005. Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika. Uredil Douglas Figueroa (USB).
Larson, r. Izračun z analitično geometrijo. 2. mesto. Izdaja. McGraw Hill.
Mathonline. Vektorske funkcije. Okrevano od: Mathonline.Wikidot.com.
OpenTAX. Proračun, količina 3. Pridobljeno iz: OpenStax.org.
Purcell, e. J. 2007. Izračun. Pearson Education.