Lastnosti logaritmične funkcije, primeri, vaje

The Logaritmična funkcija To je matematični odnos, ki povezuje vsako pozitivno resnično število x S svojim logaritmom in na bazi do. Ta odnos ustreza zahtevam, da je funkcija: vsak element X, ki pripada domeni, ima edinstveno sliko.

Zato:

f (x) = y = dnevnik_do x , Z a> 0 in drugačno od 1.

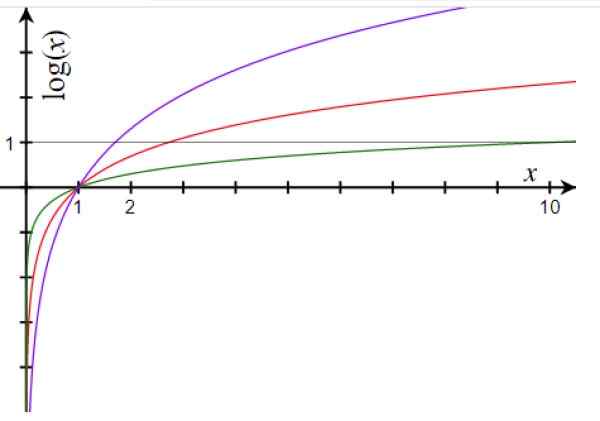
Slika 1. Graf funkcije logaritma za bazo 10 (zelena), osnovo E (rdeča) in osnovo 1.7 (vijolična). Vir: Wikimedia Commons.

Glavne lastnosti logaritmične funkcije so:

-Njegova domena so vsi večji od 0, ne vključno z 0. Z drugimi besedami, na nobeni bazi ni logaritma ali negativnih številk. V obliki intervala:

Sonce _F = (0, ∞+)

-Logaritem števila je lahko negativen, pozitiven ali 0, tako da je njen razpon ali pot:

Rgo _F = (-∞, ∞+)

-Logaritmična funkcija vedno raste za A> 1 in se zmanjšuje<1.

-Inverzno od f (x) = dnevnik_do x je eksponentna funkcija.

Dejansko je funkcija logaritma, ki temelji na inverzni funkciji potencialne funkcije:

F^-1(x) = aⁱⁿ

Od logaritma do številke x, To je številka in na katero je treba dvigniti bazo do dobiti x.

-Osnovni logaritem je vedno 1. Tako graf f (x) = dnevnik_do x Vedno se sekajo na osi x na točki (1.0)

-Logaritmična funkcija je transcendentni in je ni mogoče izraziti kot polinom ali kot količnik teh. Poleg logaritma ta skupina med drugim vključuje trigonometrične in eksponentne funkcije.

[TOC]

Primeri

Logaritmično funkcijo je mogoče vzpostaviti z različnimi osnovami, vendar je najbolj uporabljena 10 in in, kje in To je število Eulerja, ki je enako 2.71828 .. .

Ko se uporabi baza 10, se logaritem imenuje decimalni logaritem, vulgarni logaritem, briggs ali preprosto logaritem za suho.

In če se uporablja številka E, se imenuje neperijski logaritem, John Napier, škotski matematik, ki je odkril logaritme.

Vam lahko služi: multiplikativno inverzno: razlaga, primeri, rešene vaje

Zapis, ki se uporablja za vsakega, je naslednji:

-Decimalni logaritem: dnevnik₁₀ x = log x

-Neperijski logaritem: ln x

Ko bo uporabljena druga osnova, je nujno potrebna. Na primer, če gre za logaritme na bazi 2, je napisano:

y = dnevnik₂ x

Poglejmo logaritem številke 10 v treh različnih bazah, da ponazorimo to točko:

Dnevnik 10 = 1

ln 10 = 2.30259

dnevnik₂ 10 = 3.32193

Skupni kalkulatorji prinašajo samo decimalne logaritme (dnevnik) in neperijski logaritem (funkcija LN). Na internetu obstajajo kalkulatorji z drugimi bazami. Vsekakor lahko bralec s pomočjo istega preveri, da je s prejšnjimi vrednostmi izpolnjen:

10¹ = 10

in^2.3026 = 10.0001

2^3.32193 = 10.0000

Majhne decimalne razlike so posledica količine decimalk, ki so jih vzeli pri izračunu logaritma.

Prednosti logaritmov

Med prednosti uporabe logaritmov je enostavnost, ki jo zagotavljajo za delo z velikimi številkami, pri čemer uporabijo svoj logaritem namesto neposredno številke.

To je mogoče, ker funkcija logaritma raste počasneje, saj so številke večje, kot cenimo v grafiki.

Tudi v primeru zelo velikega števila so njihovi logaritmi veliko manjši, manipuliranje z majhnimi številkami pa je vedno lažje.

Poleg tega logaritmi izpolnjujejo naslednje lastnosti:

-Izdelek: dnevnik (a.b) = log a + dnevnik b

-Količnik: dnevnik (a/b) = dnevnik a - dnevnik b

-Moč: dnevnik a^b = b.dnevnik a

In na ta način izdelki in količniki postanejo vsote in odštevanje manjših števil, medtem ko se potencial pretvori v preprost izdelek, čeprav je moč visoka.

Zato logaritmi omogočajo izražanje številk, ki se razlikujejo v zelo velikih vrednostih, kot so intenzivnost zvoka, pH raztopine, svetlost zvezd, električna odpornost in intenzivnost potresa na Richterju lestvica.

Vam lahko služi: zunanji nadomestni koti: vaje in vaje rešeneSlika 2. Logaritmi se uporabljajo na Richter lestvici za količinsko določitev obsega potresa. Slika prikazuje stavbo, ki se je med potresom leta 2010 zrušila v Concepciónu v Čilu. Vir: Wikimedia Commons.

Poglejmo primer ravnanja z lastnostmi logaritmov:

Primer

Poiščite vrednost x v naslednjem izrazu:

dnevnik (5x +1) = 1 + dnevnik (2x-1)

Odgovor

Tu imamo logaritmično enačbo, glede na dejstvo, da je neznano na argumentu logaritma. Rešeno je tako, da pustite en sam logaritem na vsaki strani enakosti.

Začnemo z namestitvijo vseh izrazov, ki vsebujejo "x" levo od enakosti, in tistimi, ki vsebujejo samo številke na desni:

dnevnik (5x+1) - log (2x -1) = 1

Na levi imamo odštevanje dveh logaritmov, ki jih lahko zapišemo kot logaritem količnika:

dnevnik [(5x+1)/ (2x-1)] = 1

Vendar je na desni številka 1, ki jo lahko izrazimo kot dnevnik 10, kot smo videli prej. Tako:

dnevnik [(5x+1)/ (2x-1)] = log 10

Da se enakost izpolni, argumenti logaritmov morajo biti enaki:

(5x+1)/ (2x-1) = 10

5x + 1 = 10 (2x - 1)

5x + 1 = 20 x - 10

-15 x = -11

x = 11/15

Vaja za prijavo: Richterjeva lestvica

Leta 1957 se je v Mehiki zgodil potres, katere velikost je bila 7.7 na Richter lestvici. Leta 1960 se je v Čilu zgodil še en potres z največjo velikostjo, 9.5.

Izračunajte, kolikokrat je bil čilski potres bolj intenzivnejši kot v Mehiki, vedoč, da je velikost m_R Na Richter lestvici jo daje formula:

M_R = dnevnik (10⁴ Yo)

Rešitev

Velikost v Richterjevi lestvici potresa je logaritmična funkcija. Izračunali bomo intenzivnost vsakega potresa, saj imamo Richterjeve magnitude. Naredimo korak za korakom:

Vam lahko služi: Primo številke: značilnosti, primeri, vaje

-Mehika: 7.7 = dnevnik (10⁴ Yo)

Ker je obratna funkcija logaritma eksponentna, to uporabljamo na obeh straneh enakosti z namenom čiščenja I, ki ga najdemo v argumentu logaritma.

Ker so decimalni logaritmi, je osnova 10. Tako:

V obdobju desnice, 10 in log (10⁴ I) Odpovedani so (kot pri kvadratnem in kvadratnem korenju), ki so: zapušča:

10 ^7.7 = 10⁴ Yo

Intenzivnost Mehičnega potresa je bila:

Yo_M = 10 ^7.7 / 10⁴ = 10^3.7

 -Čili: 9.5 = dnevnik (10⁴ Yo)

Isti postopek nas vodi do intenzivnosti čilskega potresa i_Pogl:

Yo_Pogl = 10 ^9.5 / 10⁴ = 10^5.5

 Zdaj lahko primerjamo obe intenzivnosti:

Yo_Pogl / Yo_M = 10^5.5 / 10^3.7 = 10^1.8 = 63.1

 Yo_Pogl = 63.1. Yo_M

Čilijev potres je bil približno 63 -krat bolj intenzivnejši od Mehike. Ker je velikost logaritmična, raste počasneje kot intenzivnost, zato razlika v velikosti pomeni 10 -krat večjo amplitudo potresnega vala.

Razlika med magnitudami obeh potresov je 1.8, zato bi lahko pričakovali razliko v intenzivnosti, ki je bližje 100 kot 10, kot se je učinkovito zgodilo.

Pravzaprav, če bi bila razlika natančno 2, bi bil čilski potres 100 -krat bolj intenzivnejši od Mehičana.

Reference

1. Carena, m. 2019. Priročnik za matematiko prednavdljivosti. Nacionalna univerza na obali.
2. Figuera, j. 2000. Matematika 1. Raznoliko leto. Co-Bo izdaje.
3. Jiménez, r. 2008. Algebra. Dvorana Prentice.
4. Larson, r. 2010. Izračun spremenljivke. 9na. Izdaja. McGraw Hill.
5. Stewart, J. 2006. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.