Koncept naključnega eksperimenta, prostor vzorca, primeri

Tam se pogovarja naključni poskus Kadar je rezultat vsakega določenega preskušanja nepredvidljiv, tudi če je mogoče določiti verjetnost pojavljanja določenega rezultata.

Vendar je treba razjasniti, da v vsakem preskusu poskusa ni mogoče reproducirati enakega rezultata naključnega sistema z enakimi začetnimi parametri in pogoji.

Slika 1. Izstrelitev koc je naključni poskus. Vir: Pixabay.

Dober primer naključnega poskusa je izstrelitev kocke. Tudi ko poskrbite, da kocke zaženete na enak način, bo v vsakem poskusu dosežen nepredvidljiv rezultat. Pravzaprav je edino, kar lahko potrdimo, da je rezultat lahko nekaj naslednjega: 1, 2, 3, 4, 5 ali 6.

Izstrelitev valute je še en primer naključnega eksperimenta z le dvema možnima rezultatima: obraz ali pečat. Čeprav se valuta sproži z enake višine in na enak način, bo vedno prisoten faktor možnosti, kar povzroči negotovost za vsak nov poskus.

Nasprotno od naključnega poskusa je deterministični poskus. Na primer, znano je, da je vsakič, ko voda kuha na morskem nivoju, temperatura vrelišča 100 ° C. Nikoli pa se ne zgodi, da je ohranitev enakih pogojev rezultat včasih 90 ° C, še 12 0 ° C in včasih 100 ° C.

[TOC]

Vzorčni prostor

Nabor vseh možnih rezultatov naključnega poskusa se imenuje Vzorčni prostor. V naključnem poskusu izstrelitve kocke je vzorčni prostor:

D = 1, 2, 3, 4, 5, 6.

Svoje strani je ob uvedbi valute vzorčni prostor:

M = obraz, tesnilo.

Dogodek ali dogodek

V naključnem poskusu a dogodek Je pojav ali ne določenega rezultata. Na primer, v primeru predstavitve valute naj bi bil dogodek ali dogodek drag.

Vam lahko služi: homologne strani

Drug dogodek v naključnem poskusu bi lahko bil naslednji: da se ob izstrelitvi kocke izda število manj kot tri.

V primeru, da se dogodek zgodi, je nabor možnih rezultatov niz:

E = 1, 2, 3

Po drugi strani je to podskupina prostora ali vzorčnega niza:

M = 1, 2, 3, 4, 5, 6.

Primeri

Spodaj je nekaj primerov, ki ponazarjajo zgoraj:

Primer 1

Predpostavimo, da sta vržena dva kovanca, drug za drugim. Zahteva se:

a) Navedite, ali gre za naključni poskus ali na nasprotno deterministični poskus.

b) Kakšen je vzorec tega poskusa?

c) Navedite celoten dogodek A, ki ustreza poskusu, ima rezultat obraza in žiga.

d) Izračunajte verjetnost, da se dogodek pojavi.

e) Končno poiščite verjetnost, da se dogodek B: ne prikaže z rezultatom.

Rešitev 

a) To je naključni eksperiment, ker ni mogoče napovedati, kaj bo posledica izstrelitve obeh kovancev.

b) Vzorčni prostor je niz vseh možnih rezultatov:

S = (c, c), (c, s), (s, c), (s, s)

c) Dogodek A, v primeru, ki je naveden, ima lahko naslednje rezultate:

A = (c, s), (s, c)

D) Verjetnost dogodka A je pridobljena z deljenjem števila elementov niza A med številom elementov niza, ki ustreza vzorčnemu prostoru:

P (a) = 2/4 = ½ = 0.5 = 50%

e) Nabor možnih rezultatov, ki ustreza dogodku B (ki se ne pojavlja obraz, je:

Vam lahko postreže: popoln kvadratni trinomial

B = (s, s)

Torej verjetnost, da se dogodek B pojavi v eseju, je razmerje med številom možnih rezultatov B med številom skupnih primerov:

P (b) = ¼ = 0.25 = 25%.

Primer 2

Torba vsebuje 10 belih marmorjev in 10 črnih marmorjev. Iz vrečke so naključno odstranjeni in ne da bi v notranjosti tri marmorja zaporedno pogledali. 

a) Določite vzorčni prostor tega naključnega poskusa.

b) Določite nabor rezultatov, ki ustrezajo dogodku, ki je po poskusu dva črna frnikola.

c) Dogodek B naj pridobi vsaj dva črna marmorja, določite niz B rezultatov za ta dogodek.

d) kakšna je verjetnost, da se dogodek zgodi?

e) Poiščite verjetnost, da dogodek B.

f) Določite verjetnost, da je rezultat naključnega poskusa ta, da je vsaj en črni marmor. Ta dogodek se bo imenoval C.

Slika 2. Črni in črni marmori za naključne poskuse. Vir: Needpix.

Rešitev

Za izdelavo vzorčnega prostora je koristno narediti drevesni diagram, kot je tisti, prikazan na sliki 3:

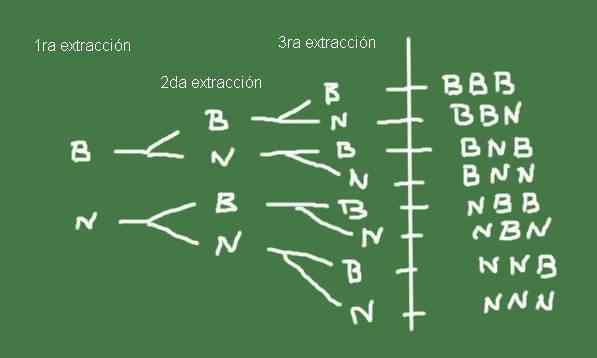Slika 3. Drevesni diagram na primer 2. Pripravila Fanny Zapata.

Ω nabor možnih rezultatov pridobivanja treh frnikolov iz vrečke z enakim številom črnih in črnih marmorjev je natančno vzorčni prostor tega naključnega poskusa.

Ω = (b, b, b), (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n) , (n, n, b), (n, n, n)

Rešitev b

Nabor možnih rezultatov, ki ustrezajo dogodku A, ki je sestavljen iz dveh črnih frnikolov, je:

Vam lahko služi: vsota Riemanna: Zgodovina, formule in lastnosti, vaje

A = (b, n, n), (n, b, n), (n, n, b)

Rešitev c

Dogodek B je opredeljen kot: "imeti vsaj dva črna marmorja, potem ko je naredil naključno ekstrakcijo treh". Nabor možnih rezultatov za dogodek B je:

B = (b, n, n), (n, b, n), (n, n, b), (n, n, n)

Rešitev d

Verjetnost dogodka A je razmerje med številom možnih rezultatov za ta dogodek in skupnim številom možnih rezultatov, to je število vzorčnih vesoljskih elementov.

P (a) = n (a) / n (ω) = 3/8 = 0.375 = 37.5%

Torej jih je 37.5% verjetnost, da boste imeli dva črna marmor po naključnem izvlečeni trije marmorji iz torbe. Vendar upoštevajte, da nikakor ne moremo napovedati natančnega rezultata poskusa.

Rešitev e

Verjetnost, da je naveden dogodek B, sestavljen iz vsaj enega črnega marmorja, je:

P (b) = n (b) / n (ω) = 4/8 = 0.5 = 50%

To pomeni, da je možnost dogodka B enaka verjetnosti, ki se ne zgodi. 

Rešitev f

Verjetnost, da dobite vsaj en črni marmor, potem ko je izvlekel tri, je enaka 1 manjša verjetnost, da je rezultat "trije beli marmorji".

P (c) = 1 - p (b b b) = 1 - ⅛ = ⅞ = 0.875 = 87.5%

Zdaj lahko preverimo ta rezultat in ugotovimo, da je število možnosti glede na dogodek C enako številu elementov možnih rezultatov za dogodek C:

C = (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n), (n, n, b) , (n, n, n)

N (c) = 7

P (c) = n (c) / n (ω) = ⅞ = 87.5%

Reference

1. Canalphi. Naključni poskus. Obnovil od: YouTube.com.
2. Matematika. Naključni poskus. Obnovil od: YouTube.com
3. Pishro Nick H . Uvod v verjetnost. Pridobljeno iz: Verjetnost.com
4. Ross. Verjetnost in statistika za inženirje. MC-Graw Hill.
5. Wikipedija. Eksperiment (teorija verjetnosti). Pridobljeno iz: v.Wikipedija.com
6. Wikipedija. Deterministični dogodek. Okrevano od: je. Wikipedija.com
7. Wikipedija. Naključni poskus. Okrevano od: je.Wikipedija.com