Formule hipergeometrične porazdelitve, enačbe, model

The hipergeometrična porazdelitev Gre za diskretno statistično funkcijo, primerno za izračun verjetnosti v naključnih poskusih z dvema možnima rezultatima. Pogoj, potreben za njegovo uporabo. 

Torej, ko je izbran za element populacije, da bi spoznal rezultat (resničen ali napačen) določene značilnosti, tega istega elementa ni mogoče več izbrati.

Slika 1. V populaciji, kot je ta, zagotovo obstajajo pokvarjeni vzorci. Vir: Pixabay.

Zagotovo je naslednji izbrani element večja verjetnost, da bo dosegel resničen rezultat, če je imel prejšnji element negativen rezultat. To pomeni, da je verjetnost različna, kolikor se elementi vzorca izvlečejo.

Glavne aplikacije hipergeometrične porazdelitve so: nadzor kakovosti v procesih z malo populacije in izračun verjetnosti v naključnih igrah.

Kar zadeva matematično funkcijo, ki definira hipergeometrično porazdelitev, to je sestavljeno iz treh parametrov, ki so:

- Številka elementov prebivalstva (n)

- Velikost vzorca (m) 

- Število dogodkov v celotni populaciji z ugodnim (ali neugodnim) rezultatom značilnosti preučene (n).

[TOC]

Formule in enačbe

Formula hipergeometrične porazdelitve daje verjetnost Str o čem x Primerni primeri določene značilnosti. Način matematičnega pisanja, odvisno od kombinatoričnih številk je:

V prejšnjem izrazu N, n in m So parametri in x sama spremenljivka. 

-Skupna populacija je N.

-Število pozitivnih rezultatov določene binarne značilnosti glede na skupno populacijo je n.

-Število elementov vzorca je m.

V tem primeru, X To je naključna spremenljivka, ki ima vrednost x in P (x) označuje verjetnost pojavljanja x ugodni primeri preučene značilnosti.

Pomembne statistične spremenljivke

Druge statistične spremenljivke za hipergeometrično porazdelitev so:

- Polovica μ = m*n/n

- Odstopanje σ^2 = m*(n/n)*(1-n/n)*(n-m)/(n-1)

- Tipično odstopanje σ ki je kvadratni koren variance.

Model in lastnosti 

Če želite priti do hipergeometričnega modela porazdelitve, temelji na verjetnosti pridobitve x ugodni primeri v vzorcu velikosti m. Ta vzorec vsebuje elemente, ki izpolnjujejo posest, ki se preučuje, in elemente, ki ne.

Spomnimo se tega n predstavlja število ugodnih primerov v celotni populaciji N predmete. Potem bi bila verjetnost izračunana tako:

Vam lahko služi: vektorski prostor: baza in dimenzija, aksiomi, lastnosti

P (x) = (# načinov za pridobitev x# na neuspele načine)/(# Skupni načini izbire)

Če izrazite zgoraj v obliki kombinatoričnih števil, je dosežen naslednji model distribucije verjetnosti:

Glavne lastnosti hipergeometrične porazdelitve

So naslednje:

- Vzorec mora biti vedno majhen, čeprav je populacija velika.

- Elementi vzorca se izvlečejo iz enega, ne da bi jih ponovno vključili v populacijo.

- Nepremičnina, ki jo je treba preučiti, je binarna, to je, da lahko vzame le dve vrednosti: 1 tudi 0, O dobro PRAV tudi Lažne.

V vsakem koraku ekstrakcije se verjetnost spremeni, odvisno od prejšnjih rezultatov.

Pristop z binomno porazdelitvijo

Druga lastnost hipergeometrične porazdelitve je, da se lahko obrne na binomno porazdelitev, označeno kot Bi, Dokler je prebivalstvo N biti velik in vsaj 10 -krat večji od vzorca m. V tem primeru bi bilo tako:

P (n, n, m; x) = bi (m, n/n, x)           

Dokler je n velik in n> 10m

Primeri

Primer 1

Recimo, da stroj, ki proizvaja vijake in nakopičene podatke, kaže, da 1% izhaja z napakami. Potem bo v škatli z n = 500 vijaki število napak:

N = 500 * 1/100 = 5

Verjetnosti s hipergeometrično porazdelitvijo

Recimo, da iz tistega polja (torej tega populacije) vzamemo vzorec M = 60 vijakov.

Verjetnost, da ni vijaka (x = 0) vzorca okvarjena 52,63%. Ta rezultat je dosežen pri uporabi hipergeometrične funkcije porazdelitve:

P (500, 5, 60; 0) = 0,5263

Verjetnost, da je x = 3 vzorčni vijaki okvarjeni, je: P (500, 5, 60; 3) = 0,0129.

Po drugi strani je verjetnost, da je X = 4 vijaki šestdesetih let vzorca okvarjena: P (500, 5, 60; 4) = 0,0008.

Končno je verjetnost, da se x = 5 vijakov v tem vzorcu pojavijo z napako, je: P (500, 5, 60; 5) = 0.

Če pa želite vedeti verjetnost, da je v tem vzorcu več kot 3 pokvarjene vijake, potem je treba pridobiti nakopičeno verjetnost in dodati:

P (3)+P (4)+P (5) = 0,0129+0,0008+0 = 0,0137.

Ta primer je prikazan na sliki 2, pridobljen z uporabo Geogebra Široka uporaba brezplačna programska oprema v šolah, inštitutih in univerzah.

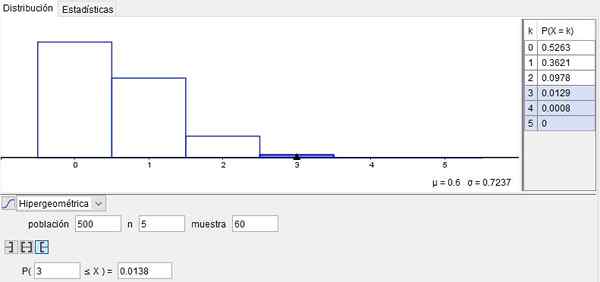Slika 2. Primer hipergeometrične porazdelitve. Pripravil f. Zapata z geogebro.

Primer 2

Španska paluba ima 40 kart, od tega 10 zlata, preostalih 30 pa jih nima. Recimo, da se iz tega krova izvleče 7 kart, ki se ne vrnejo na palubo.

Vam lahko služi: centralna simetrija: lastnosti, primeri in vaje

Če je X število zlatov, ki so prisotni v 7 izvlečenih karticah, potem je verjetnost, ki je X oros v ekstrakciji 7 kartic, poda s hipergeometrično porazdelitvijo p (40,10,7; x).

Poglejmo to: Če želite izračunati verjetnost, da bomo imeli 4 zlate v ekstrakciji 7 kartic, uporabljamo formulo hipergeometrične porazdelitve z naslednjimi vrednostmi:

In rezultat je: 4,57% verjetnost.

Če pa želite vedeti, da boste pridobili več kot 4 kartice, bomo morali dodati:

P (4)+p (5)+p (6)+p (7) = 5,20%

Rešene vaje

Naslednji niz vaj je namenjen ponazoritvi in ​​asimilaciji konceptov, ki so bili predstavljeni v tem članku. Pomembno je, da jih bralec poskuša rešiti sam, preden pogleda rešitev.

Vaja 1

Ugotovila je, da je profilaktična tovarna vsakih 1000 kondomov, ki jih proizvaja določen stroj, 5 pokvarjenih. Za izvedbo nadzora kakovosti se naključno sprejmejo 100 kondomov in se parcela zavrne, če je vsaj eden ali več pokvarjenih. Odgovor:

a) Kakšna možnost mora biti 100 zavržena?

b) Ali je to merilo za nadzor kakovosti učinkovito?

Rešitev

V tem primeru se bodo pojavile zelo velike kombinatorične številke. Izračun je težaven, razen če je na voljo ustrezen računalniški paket.

Ker pa gre za veliko populacijo in je vzorec desetkrat manjši od celotne populacije, lahko pristop uporabite za hipergeometrično porazdelitev zaradi binomne porazdelitve:

P (1000,5,100; x) = bi (100, 5/1000, x) = bi (100, 0.005, x) = c (100, x)*0.005^x (1-0.005)^(100-x)

V prejšnjem izrazu C (100, x) Je kombinatorična številka. Potem se bo verjetnost HAYA več kot ena pokvarjena izračunala na naslednji način:

P (x> = 1) = 1 - bi (0) = 1-.6058 = 0.3942

To je odličen pristop, če v primerjavi z vrednostjo, dobljeno pri uporabi hipergeometrične porazdelitve: 0.4102

Lahko rečemo, da je treba 40 -odstotno verjetnost veliko 100 profilaktike zavreči, kar ni zelo učinkovito.

Toda biti nekoliko manj zahtevni v postopku nadzora kakovosti in zavržene.

Vaja 2

Plastični taco stroj deluje tako, da je od vsakih 10 kosov deformiran. V vzorcu 5 -ovca mora biti možnost en kos okvarjena.

Rešitev

Prebivalstvo: n = 10

Vam lahko služi: pitagorejske identitete: demonstracija, primer, vaje

Številka n okvarjena za vsakega n: n = 1

Velikost vzorca: M = 5

P (10, 1, 5; 1) = C (1.1)*c (9.4)/c (10.5) = 1*126/22 = 0.5

Zato obstaja 50 -odstotna verjetnost, da se v vzorcu 5 taco izkaže.

Vaja 3

Na srečanju mladih srednjih šol je 7 dam in 6 gospodov. Med dekleti 4 študirajo humanistike in 3 znanosti. V skupini fantov 1 študija humanistike in 5 znanosti. Izračunajte naslednje:

a) Naključno izbira treh deklet: kakšna je verjetnost, da vsi preučujejo humanistične študije?.

b) Če so trije udeleženci naključno izbrani na sestanek prijateljev: kaj so trije, ne glede na seks, preučite tri ali humanistične tudi vse tri?.

c) Zdaj izberite dva naključna prijatelja in pokličite x Na naključno spremenljivko "Število tistih, ki preučujejo humanistike". Med dvema izbranima določite povprečno ali pričakovano vrednost x in variance σ^2.

Rešitev 

Prebivalstvo je skupno število deklet: n = 7. Tisti, ki študirajo humanistiko, so n = 4, od skupne. Naključni vzorec deklet bo m = 3.

V tem primeru je verjetnost, da so trije humanistiki, podana s hipergeometrično funkcijo:

P (n = 7, n = 4, m = 3, x = 3) = c (4, 3) c (3, 0) / c (7, 3) = 0.1143

Potem je 11.4% verjetnost, da trije naključni Chicas preučujejo humanistike.

Rešitev b

Vrednosti, ki jih je treba uporabiti, so:

-Prebivalstvo: n = 14

-Količina, v kateri preučuje črke, je: n = 6 in

-Velikost vzorca: M = 3.

-Število prijateljev, ki študirajo humanistike: x

V skladu s tem x = 3 pomeni, da trije preučujejo humanistične študije, vendar x = 0 pomeni, da nobena ne študira humanistike. Verjetnost, da tri študije isto daje vsota:

P (14, 6, 3, x = 0) + p (14, 6, 3, x = 3) = 0.0560 + 0.1539 = 0.2099

Nato imamo 21 -odstotno verjetnost, da trije udeleženci sestankov, izbrani naključno, preučijo isto.

Rešitev c

Tu imamo naslednje vrednosti:

N = 14 skupnih populacij prijateljev, n = 6 skupnega števila v populaciji, ki preučuje humanistično, velikost vzorca je M = 2.

Upanje je:

E (x) = m * (n/n) = 2 * (6/14) = 0.8572

In variance:

σ (x)^2 =  m*(n/n)*(1-n/n)*(n-m)/(n-1) = 2*(6/14)*(1-6/14)*(14-2)/(14 -1) =

= 2*(6/14)*(1-6/14)*(14-2)/(14-1) = 2*(3/7)*(1-3/7)*(12) (13)  = 0.4521

Reference

1. Diskretne porazdelitve verjetnosti. Okrevano od: biploot.USAL.je
2. Statistika in verjetnost. Hipergeometrična porazdelitev. Pridobljeno iz: ProjectOdescartes.org
3. Cdpye-ugr. Hipergeometrična porazdelitev. Okreval od: ugr.je
4. Geogebra. Klasična geogebra, izračun verjetnosti. Okreval od Geogebre.org
5. Enostaven preizkus. Rešene hipergeometrične distribucijske vaje. Okrevano od: Probafacil.com
6. Minitab. Hipergeometrična porazdelitev. Pridobljeno iz: Podpora.Minitab.com
7. Univerza v Vigo. Glavne diskretne distribucije. Okrevano od: anapg.spletna mesta.Uvigo.je
8. Vittor. Statistika in kombinatorična. Pridobljeno od: Vititor.mreža
9. Weisstein, Eric W. Hipergeometrična porazdelitev. Okreval od: Mathworld.Wolfram.com
10. Wikipedija. Hipergeometrična porazdelitev. Okrevano od: je.Wikipedija.com