Empirično pravilo, kako ga uporabiti, za kaj je to, rešene vaje

A Empirično pravilo Je rezultat praktične izkušnje in opazovanja resničnega življenja. Na primer, lahko veste, da lahko vrste ptic opazimo na določenih mestih v vsakem letnem času in da je mogoče določiti "pravilo", ki opisuje življenjske cikle teh ptic.

V statistiki se empirično pravilo nanaša na obliko združevanja opazovanj okoli osrednje vrednosti, povprečnega ali povprečnega, v enotah za standardno odstopanje.

Recimo, da imate skupino ljudi s povprečno višino 1.62 metrov in standardni odklon 0.25 metrov, potem bi empirično pravilo omogočilo, da na primer določimo, koliko ljudi bi bilo v intervalu povprečnega bolj ali manj standardnega odklona?

V skladu s pravilom je 68% podatkov bolj ali manj standardni odklon povprečja, torej 68% ljudi bo imelo višino med 1.37 (1.62-0.25) in 1.87 (1.62+0.25) metrov.

[TOC]

Od kod prihaja empirično pravilo?

Empirično pravilo je posploševanje teorema Tchebysheva in normalne porazdelitve.

Tchebyshev teorem

Tchebyshev teorem pravi, da: za neko vrednost K> 1 je verjetnost, da je naključna spremenljivka med povprečnimi manjšimi K -krat večjo odstopanje, povprečni več K krat, standardni odklon je večji ali enak (1 -1 /k²).

Prednost tega teorema je, da velja za diskretne ali neprekinjene naključne spremenljivke s kakršno koli porazdelitvijo verjetnosti, vendar pravilo, opredeljeno iz njega, ni vedno zelo natančno, saj je odvisno od simetrije porazdelitve. Bolj kot asimetrična je porazdelitev naključne spremenljivke, manj prilagojena pravilu.

Empirično pravilo, opredeljeno iz tega teorema, je:

Če je K = √2, se reče, da je 50% podatkov v intervalu: [µ - √2 s, µ + √2 s]

Če je K = 2, naj bi bilo 75% podatkov v intervalu: [µ - 2 s, µ + 2 S]

Če je K = 3, naj bi bilo 89% podatkov v intervalu: [µ - 3 s, µ + 3 s]

Normalna porazdelitev

Običajna porazdelitev ali Gauss Bell omogoča vzpostavitev empiričnega pravila ali pravila 68 - 95 - 99.7.

Vam lahko služi: delež

Pravilo temelji na verjetnosti pojava naključne spremenljivke v intervalih med povprečno manjšimi, dvema ali tremi standardnimi odstopanji in povprečnimi plus enim, dvema ali tremi standardnimi odstopanji.

Empirično pravilo določa naslednje intervale:

68.27% podatkov je v intervalu: [µ - s, µ + s]

95.45% podatkov je v intervalu: [µ - 2s, µ + 2s]

99.73% podatkov je v intervalu: [µ - 3s, µ + 3s]

Na sliki lahko vidite, kako so predstavljeni ti intervali in razmerje med njimi s povečanjem širine grafične baze.

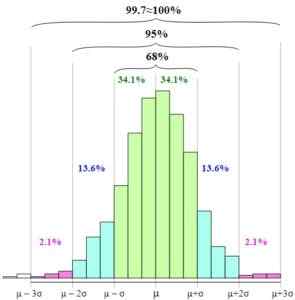Empirično pravilo. Melikamp [cc by-sa 4.0 (https: // creativeCommons.org/)] Standardizacija naključne spremenljivke, to je izražanje naključne spremenljivke v smislu standardne ali normalne spremenljivke, poenostavi uporabo empiričnega pravila, saj ima spremenljivka z povprečno enaka nič in standardni odklon enaka do enega.

Zato uporaba empiričnega pravila na lestvici standardne normalne spremenljivke z določa naslednje intervale:

68.27% podatkov je v intervalu: [-1, 1]

95.45% podatkov je v intervalu: [-2, 2]

99.73% podatkov je v intervalu: [-3, 3]

Kako uporabiti empirično pravilo?

Empirično pravilo vam omogoča, da pri delu z normalno porazdelitvijo skrajšate izračune.

Recimo, da ima skupina 100 univerzitetnih študentov povprečno starost 23 let, s standardnim odklonom 2 leti. Katere informacije dopušča empirično pravilo?

Uporaba empiričnega pravila pomeni po korakih:

1- Zgradite intervale pravil

Ker je povprečje 23 in je standardni odklon 2, potem so intervali:

[µ - s, µ + s] = [23 - 2, 23 + 2] = [21, 25]

[µ - 2s, µ + 2s] = [23 - 2 (2), 23 + 2 (2)] = [19, 27]

[µ - 3s, µ + 3s] = [23 - 3 (2), 23 + 3 (2)] = [17, 29]

2- Izračunajte število študentov v vsakem intervalu glede na odstotke

(100)*68.27% = 68 študentov približno

(100)*95.45% = približno 95 študentov

(100)*99.73% = 100 študentov

3- Starost intervali so povezani s količino študentov in jih razlagajo

Vsaj 68 študentov je med 21 in 25 let.

Vam lahko služi: opisna statistika: zgodovina, značilnosti, primeri, koncepti

Vsaj 95 študentov je med 19 in 27 let.

Skoraj 100 študentov je starih med 17 in 29 let.

Za kaj je empirično pravilo?

Empirično pravilo je hiter in praktičen način za analizo statističnih podatkov, saj je vse bolj zanesljiv, če je porazdelitev blizu simetriji.

Njegova uporabnost je odvisna od polja, na katerem se uporablja, in vprašanj, ki se pojavljajo. Zelo koristno je vedeti, da je pojav vrednosti treh standardnih odstopanj skoraj malo verjetno pod ali nadpovprečno, tudi za ne -nermalne spremenljivke porazdelitve, vsaj 88.8% primerov je v treh intervalu Sigma.

V družbenih vedah je na splošno prepričljiv rezultat interval povprečne več ali manj dve sigmi (95%), medtem ko v fiziki delcev nov učinek zahteva pet interval Sigmas (99.99994%), da se šteje za odkritje.

Rešene vaje

Zajci v rezervatu

V rezervatu za prostoživeče živali se ocenjuje, da je v povprečju 16.000 zajcev s standardnim odklonom 500 zajcev. Če porazdelitev spremenljivke 'število zajcev v rezervat' ni znana, ali je mogoče.000 in 17.000 zajcev?

Interval je mogoče predstaviti v teh pogojih:

15000 = 16000 - 1000 = 16000 - 2 (500) = µ - 2 s

17000 = 16000 + 1000 = 16000 + 2 (500) = µ + 2 s

Zato: [15000, 17000] = [µ - 2 s, µ + 2 s]

Z uporabo teorema Tchebysheva obstaja verjetnost vsaj 0.75, da je populacija zajcev rezervata za prostoživeče živali med 15.000 in 17.000 zajcev.

Povprečja otrok iz države

Povprečna teža eneletne otroke je običajno razporejena s povprečno 10 kilogrami in standardnim odklonom približno 1 kilogram.

a) Ocenite odstotek otrok v državi, ki imajo povprečno težo med 8 in 12 kilogramov.

8 = 10 - 2 = 10 - 2 (1) = µ - 2 s

12 = 10 + 2 = 10 + 2 (1) = µ + 2 s

Zato: [8, 12] = [µ - 2s, µ + 2s]

Lahko vam služi: Tukey Test: Kaj je v primeru, da je v primeru rešena vaja

Po empiričnem pravilu je mogoče potrditi, da 68.27% otrok v državi ima med 8 in 12 kilogramov teže.

b) kakšna je verjetnost, da najdete enega leta, starih 7 kilogramov ali manjše teže?

7 = 10 - 3 = 10 - 3 (1) = µ - 3 s

Znano je, da 7 kilogramov teže predstavlja vrednost µ - 3s, prav tako pa je znano, da je 99.73% otrok je med 7 in 13 kilogrami teže. To odide le 0.27% vseh otrok za skrajnost. Polovica, 0.135%, ima 7 kilogramov teže ali manj, druga polovica pa 0.135%, ima 11 kilogramov teže ali več.

Torej, lahko sklepamo, da obstaja verjetnost 0.00135, da ima otrok 7 kilogramov teže ali manj.

c) Če prebivalstvo države doseže 50 milijonov prebivalcev in otroke 1 leta?

9 = 10 - 1 = µ - s

11 = 10 + 1 = µ + s

Zato: [9, 11] = [µ - s, µ + s]

Po empiričnem pravilu 68.27% enega do starejših otrok je v intervalu [µ -s, µ + s]

V državi je 500.000 otrok enega leta (1% od 50 milijonov), torej 341350 otrok (68.27% od 500000) ima med 9 in 11 kilogramov teže.

Reference

1. Abraira, v. (2002). Standardni odklon in standardna napaka. Revija Semergen. Splet je bil obnovljen.Arhiv.org.
2. Freund, r.; Wilson, w.; Mohr, d. (2010). Statistične metode. Tretji ed. Academic Press-Ellevier Inc.
3. Server Alicante (2017). Empirično pravilo (statistični izrazi). Slovar je bil obnovljen.Server-Alive.com.
4. Lind, d.; Marchal, w.; Wathen, s. (2012). Statistični podatki, ki se uporabljajo za podjetja in gospodarstvo. Deseti izd. McGraw-Hill/Medamerican iz Mehike S. Do.
5. Salinas, h. (2010). Statistika in verjetnosti. Okreval od UDA.Cl.
6. Sokal, r.; Rohlf, f. (2009). Uvod v biostatistiko. Drugi ed. Dover Publications, Inc.
7. Spiegel, m. (1976). Verjetnost in statistika. Serija Schaum. McGraw-Hill/Medamerican iz Mehike S. Do.
8. Spiegel, m.; Stephens, l. (2008). Statistika. Četrti Ed. McGraw-Hill/Medamerican iz Mehike S. Do.
9. Pregled STAT119 (2019). Vprašanja o pravilih empiričnega reševanja. Pridobljeno iz STAT119Review.com.
10. (2019). 68-95-99.7 pravilo. Pridobljeno iz.Wikipedija.org.