Ocena po presledkih

Kakšna je ocena po presledkih?

The Ocena po presledkih To je način, kako določiti obseg vrednosti, v katerih je mogoče vključiti povprečje populacije, na podlagi informacij vzorca končne velikosti, naključno izvlečene iz celotne populacije.

On Interval ocenjevanja Je nižji, saj je vzorec večji, vendar postane širši, če raven ali odstotek zanesljivosti istega povečanja.

Če želite vedeti, da je povprečje prebivalstva določene spremenljivke v natančni obliki, potem je treba upoštevati celotno populacijo, nekaj, kar ni vedno izvedljivo, saj če gre za zelo veliko populacijo celotna populacija. Zaradi tega se uporablja en ali več naključnih vzorcev celotne populacije.

Temelji na hipotezi, da mora biti s pridobivanjem naključnega vzorca, ki ni pristransko in upoštevanje sorazmerno vse sloje, povprečna vrednost vzorca zelo blizu vrednosti povprečnega prebivalstva.

Logika kaže, da večja kot so vzorčni podatki, razlika med povprečno vrednostjo vzorca in povprečno vrednostjo populacije je nižja.

Interval ocenjevanja

V praksi, razen če je celotna populacija znana, je mogoče z nekaj verjetnosti najti le interval, kjer je mogoče najti povprečno prebivalstvo, na podlagi vzorca končne velikosti.

V primeru populacije, ki sledi normalni porazdelitvi, z Standardni odklon σ , the Standardna razlika Med povprečnim prebivalstvom μ in povprečni vzorec velikosti n daje:

| μ - | ≤ σ / √n

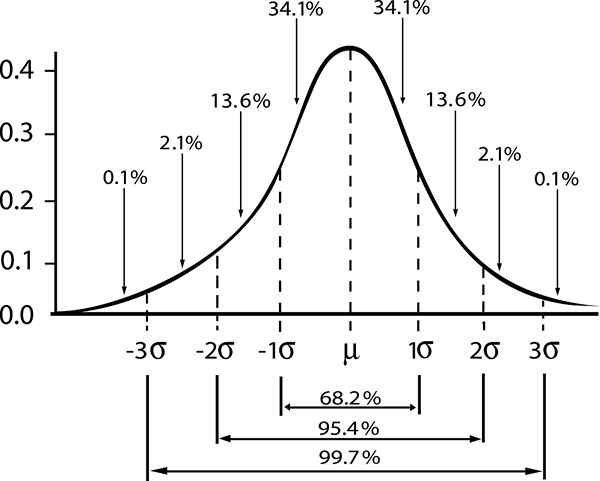
Tu beseda "standard" kaže, da je 68% vzorcev velikosti n, Imajo povprečno vrednost med intervalom [μ - σ / √n, μ + σ / √n].

Vam lahko služi: merila delitve: kaj so, kakšna so uporaba in pravila

Standardna ocena

Alternativna razlaga zgoraj navedenega bi bila, da pomeni, da povprečna populacija, pridobljena iz vzorca velikosti n in povprečna vrednost se razume v intervalu  [ - σ / √n, + σ / √n], S 68% verjetnostjo.

V večini resničnih primerov ni mogoče poznati standardnega odstopanja populacije, torej σ Približno je s standardnim odklonom vzorca s, ki se izračuna na naslednji način:

S = √ (∑ (x_Yo - )² / √ (n-1).

Od tam dobite interval, ki bi lahko vseboval povprečje prebivalstva s 68 -odstotno stopnjo zaupanja (standardna stopnja zaupanja), ki jo je dal:

  -s / √n ≤ μ ≤ + s / √n

Ta interval merjenja populacije je znan kot standardni interval ocenjevanja in je bil pridobljen samo s podatki, ki so na voljo v velikosti n.

Iz prejšnje formule izhaja, da je, če želite okrepiti interval ocenjevanja na polovici četverico Velikost vzorca.

Ocenjevanje intervalov zaupanja

V nekaterih študijah je standardna raven 68% lahko nezadostna, potem je treba določiti intervale s poljubno stopnjo zaupanja γ.

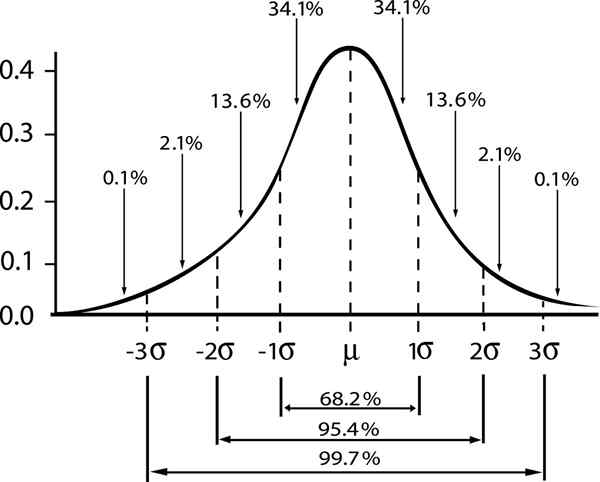Prikazano je razmerje med mejo zanesljivosti in intervalom v Gaussovi porazdelitvi

Če označujemo ε Standardna napaka s/√n, Nato ocena napake za stopnjo zaupanja γ bo dal:

E = zγ⋅ε.

Kje Zγ Gre za število, za katero se pomnoži standardna napaka in s tem pridobi mej napake s poljubno stopnjo zaupanja γ.

Da bi dobili faktor Zγ, nadaljujte na naslednji način:

Lahko vam služi: racionalne številke: lastnosti, primeri in operacije

Korak 1

Je klic raven pomembnosti α ustreza ravni zaupanja γ po naslednji formuli:

α = 1 - γ

2. korak

Vrednost je določena:

To je nabrana frekvenca v običajni porazdelitvi N (0,1) V intervalu (-∞, Zγ ].

Korak 3

Razčisti Zγ Enačba:

N (zγ) = 1 - α/2

Ker gre za integralno enačbo, se ta očistek dobi iz običajnih tabel porazdelitve z uporabo metode linearne interpolacije.

4. korak

Namesto tega je uporaba tabel, statističnih funkcij, vključenih v preglednice, kot so Excel, tudi Google Sheet. Ti programi vključujejo normalno obratno funkcijo N^-1, tako da je korekcijski faktor Zγ Dobimo neposredno ocenjevanje te obratne funkcije:

Zγ = n^-1(1 - α/2).

Tipični intervali zaupanja

Najpogosteje uporabljene stopnje zaupanja so:

• Zγ = 1; Standardna stopnja zaupanja γ = 0,68.
• Zγ = 2; stopnja zaupanja γ = 0,95 (ali stopnja pomembnosti 5%).
• Zγ = 3; stopnja zaupanja γ = 0,997 (ali 0,3%pomembnosti)

Primeri

Primer 1

Določite povprečni interval novorojenčkov v mesecu avgustu v velikem mestu, ki temelji na naključnem vzorcu 100 dojenčkov, v katerem je bila pridobljena povprečna teža 3100 gramov z vzorčnim standardnim odklonom S = 1500 gramov.

Rešitev

Najprej se določi standardna napaka vzorca:

ε = s/√n = (1500 g)/√100 = 150 g.

Zato je mogoče sklepati, da je povprečna teža dojenčkov, rojenih avgusta v tem mestu, med 2950 g in 3250 g, s 68% verjetnosti.

Primer 2

Recimo, da je velikost vzorca dojenčkov, rojenih v istem mesecu avgusta in v istem mestu primera 1. Povprečna teža vzorca je 3100 g s standardno 1500 g disperzije. 

Lahko vam služi: razgradnjo naravnega števila (primeri in vaje)

Od tega novega vzorca se zahteva, da oceni povprečni interval teže novorojenčkov tega mesta.

Rešitev

Zdaj se standardna napaka zmanjšuje v faktorju 1/√2, Torej bo nova standardna napaka povprečne teže 106 g.

Potem je mogoče oceniti, iz tega novega vzorca, da je povprečna teža novorojenčkov sestavljena v območju od 2994 g do 3206 g, s 68 -odstotno verjetnostjo.

Vaje

Vaja 1

Avgusta določite povprečni razpon novorojenčkov, začenši z vzorcem, določenim v primeru 1, z 95 -odstotno verjetnostjo.

Rešitev

95 -odstotna raven zanesljivosti podvoji povprečni razpon teže v primerjavi s 68 -odstotno stopnjo zanesljivosti.

Zato je povprečna teža novorojenčkov vključena v razpon 2800 gramov pri 3400 gramih z 95% gotovostjo.

Vaja 2

Ocenite z 99,7 -odstotno stopnjo zaupanja v interval, v katerem bo ugotovljena povprečna teža novorojenčkov iz velikega mesta, če je na voljo vzorec s povprečno težo 100 dojenčkov, ki je enaka 3100 g, in s standardnim odklonom vzorca S = 1500 g.

Rešitev

Povprečna stopnja napake z težo z 99,7% gotovosti bo potrošna povprečna napaka, to je:

3*1500/√100.

Potem iz tega vzorca sklepamo, da bo povprečna teža novorojenčkov vključena v interval: 2650 gramov do 3550 gramov, z gotovostjo 99,7%. 

Iz tega rezultata ga opazimo, saj pri večji ravni gotovosti poveča negotovost povprečne teže na veliko širši interval.