Odstotna napaka
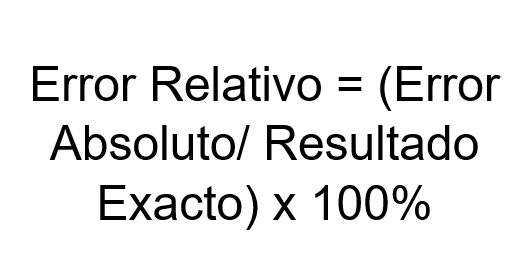
- 1695
- 415
- Stuart Armstrong
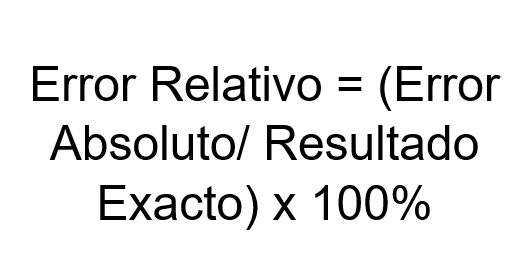
Kakšna je odstotna napaka?
On odstotna napaka Je manifestacija relativne napake v odstotkih. Z drugimi besedami, gre za numerično napako, izraženo z vrednostjo, ki daje relativno napako, nato pomnoženo s 100.
Če želite razumeti, kakšna je odstotna napaka, morate najprej razumeti, kakšna numerična napaka, absolutna napaka in relativna napaka, saj odstotek napake izhaja iz teh dveh izrazov.
Številčna napaka je tista, ki se pojavi, kadar se ukrep sprejme pri uporabi naprave (neposredna meritev) ali kadar je matematična formula (posredna mera) slabo uporabljena.
Vse številčne napake je mogoče izraziti absolutno ali odstotek. Absolutna napaka je tista, ki se pojavi pri izvajanju pristopa za predstavljanje matematične količine, ki je posledica merjenja elementa ali napačne uporabe formule.
Na ta način se natančna matematična vrednost spremeni s pristopom. Izračun absolutne napake se izvede tako, da odštejemo pristop k natančni matematični vrednosti, kot je ta:
Absolutna napaka = natančen rezultat - pristop
Mejne enote, ki se uporabljajo za manifestiranje relativne napake, so enake, ki se uporabljajo za pogovor o numerični napaki. Podobno lahko ta napaka daje pozitivno ali negativno vrednost.
Relativna napaka je količnik, pridobljen z deljenjem absolutne napake z natančno matematično vrednostjo.
Na ta način je odstotna napaka, ki jo dobimo z množenjem rezultata relativne napake na 100. Z drugimi besedami, odstotna napaka je odstotek (%) izraz relativne napake.
Vam lahko služi: x kvadratRelativna napaka = (absolutna napaka/ natančen rezultat)
Odstotna vrednost, ki je lahko negativna ali pozitivna, to je lahko vrednost, ki jo predstavlja presežek ali privzeto. Ta vrednost, za razliko od absolutne napake, ne predstavlja enot, ki presegajo odstotek (%).
Relativna napaka = (absolutna napaka/ natančen rezultat) x 100%
Poslanstvo relativnih in odstotnih napak je navesti kakovost nečesa ali zagotoviti primerjalno vrednost.
Primeri izračuna odstotne napake
1. Dve -kopenski meritev
Z merjenjem dveh sklopov ali zemljišča naj bi pri meritvi približno 1 m napake. Zemljišče je 300 metrov in drugo od 2.000.
V tem primeru bo relativna napaka prve meritve večja kot pri drugem, saj v deležu 1 m predstavlja višji odstotek.
300 m veliko:
Ep = (1/300) x 100%
EP = 0,33%
Veliko 2.000 m:
Ep = (1/2.000) x 100%
EP = 0,05%
2. Merjenje aluminija
V laboratoriju se dostavi aluminijasti blok. Pri merjenju dimenzij bloka in izračunu njegove mase in volumna je določena njegova gostota (2,68 g/cm³).
Vendar pri preverjanju numerične tabele materiala to kaže, da je gostota aluminija 2,7 g/cm³. Na ta način bi se absolutna in odstotna napaka izračunala na naslednji način:
EA = 2,7 - 2,68
EA = 0,02 g/cm³.
Ep = (0,02/2,7) x 100%
EP = 0,74%
3- Obisk dogodka
Domnevalo se je, da 1.000.000 ljudi bi šlo na določen dogodek. Vendar je bilo natančno število ljudi, ki so šli na ta dogodek, 88.000. Absolutna in odstotna napaka bi bila naslednja:
Vam lahko služi: naključna spremenljivka: koncept, vrste, primeriEa = 1.000.000 - 88.000
EA = 912.000
Ep = (912.000/1.000.000) x 100%
EP = 91,2%
4. Kroglica padec
Izračunani čas mora vzeti kroglico, da pride do tal, potem ko ga vržete na razdaljo 4 metre, 3 sekunde.
Vendar je v času eksperimentiranja ugotovljeno, da je žoga trajala 2,1 sekunde, da je dosegla tla.
Ea = 3 - 2.1
EA = 0,9 sekunde
Ep = (0,9/2.1) x 100%
EP = 42,8%
5. Potreben je avto
Ocenjuje se, da če bo avtomobil šel pri 60 km, bo dosegel cilj čez 1 uro. Vendar je v resničnem življenju avtomobil potreboval 1,2 ure, da je dosegel cilj. Odstotek napake tega časovnega izračuna bi bila izražena na naslednji način:
Ea = 1 - 1.2
EA = -0.2
Ep = (-0,2/1,2) x 100%
EP = -16%
6. Merilna dolžina
Vsaka dolžina se meri z vrednostjo 30 cm. Preverjanje merjenja te dolžine je očitno, da je prišlo do napake 0,2 cm. Odstotek napake v tem primeru bi se pokazala na naslednji način:
Ep = (0,2/30) x 100%
EP = 0,67%
7. Dolžina mostu
Izračun dolžine mostu glede na letala je 100 m. Vendar je pri potrditvi te dolžine, ko je bila zgrajena, očitno, da je dejansko dolga 99,8 m. Odstotek napake bi na ta način dokazal.
Ea = 100 - 99,8
Ea = 0,2 m
EP = (0,2/99,8) x 100
EP = 0,2%
8. Premer vijaka
Glava standardnega izdelanega vijaka je premera 1 cm.
Vam lahko služi: neprekinjena enotna porazdelitev: značilnosti, primeri, aplikacijeVendar pri merjenju tega premera opazimo, da ima vijačna glava res 0.85 cm. Odstotek napake bi bila naslednja:
Ea = 1 - 0,85
Ea = 0,15 cm
EP = (0,15/0,85) x 100
EP = 17,64%
9. Objektna teža
Glede na njegovo prostornino in materiale se ocenjuje, da je teža določenega predmeta 30 kilogramov. Ko je predmet analiziran, opazimo, da je njegova resnična teža 32 kilogramov.
V tem primeru je vrednost odstotne napake opisana na naslednji način:
Ea = 30 - 32
Ea = -2 kilogramov
Ep = (2/32) x 100
EP = 6,25%
10. Merjenje jekla
V laboratoriju se preučuje jeklena plošča. Pri merjenju dimenzij lista in izračunavanju njegove mase in volumna se določi gostota iste (3,51 g/cm³).
Vendar pri preverjanju numerične tabele materiala to kaže, da je gostota jekla 2,85 g/cm³. Na ta način bi se absolutna in odstotna napaka izračunala na naslednji način:
EA = 3,51 - 2,85
Ea = 0,66 g/cm³.
Ep = (0,66/2,85) x 100%
EP = 23,15%
Reference
- Odstotna napaka. Okreval od matematike.com
- Kako izračunati odstotno napako. Opomogel od Thoughtco.com

