Testiranje hipotez

Kaj je test hipoteze?

The testiranje hipotez, V statistiki gre za postopek, ki se uporablja za preverjanje, kako uspešna je domneva o a prebivalstvo. Te domneve se imenujejo hipoteza, da se načeloma štejejo za resnične, dokler nekateri dokazi tega ne potrjujejo ali zanikajo.

Ti dokazi zagotavljajo vzorčni podatki, tisti, ki prihajajo iz pomembnega dela populacije, imenovani vzorec. Teorija verjetnosti zagotavlja potrebne tehnike za nasprotje verodostojnosti hipotez.

Primeri hipotez so:

-Povprečna temperatura telesa človeka je 36.1 ° C.

-V povprečju slana torba z arašidi, proizvedena v tovarni prigrizkov, tehta 50 g.

-80% prebivalcev mesta je v zadnjih 6 mesecih kupilo na spletu.

-IQ testni rezultati za študente iz dobro znane ustanove imajo standardni odklon 15.

-Določena naključna spremenljivka x sledi Poissonovi porazdelitvi.

Prvi štirje so vrste hipoteze parametrični, Ker gre za izjave o nekaterih parametrov prebivalstva, kot so povprečje, standardni odklon ali nekaj deleža.

Po drugi strani pa zadnja hipoteza vzpostavi porazdelitev naključne spremenljivke, in ker se ne nanaša na nobenega parametra ali lastnosti populacije ni parametrično.

Ničelna hipoteza in alternativna hipoteza

Obstajata dve vrsti hipoteze, s katerim lahko izvedemo test, ki bo služil za njihovo kontrast:

-Ničelna hipoteza, označeno kot h₀, navaja, da ima v študiji parameter uveljavljeno vrednost ali da naključna spremenljivka sledi določeni porazdelitvi. Zato se s simbolično izražanjem ničelne hipoteze vedno uporablja simbol enakosti.

-Alternativna hipoteza: imenovan h₁, Zatrjuje, da se parameter ali porazdelitev razlikujeta od tistega, kar zagotavlja ničelna hipoteza, zato simbolično izražajo alternativno hipotezo, se simboli uporabljajo: ali ≠, vendar nikoli enakost.

Lahko vam služi: Lastnost Algebra Lock: demonstracija, primeri

Ko je nična hipoteza sprejeta, je alternativna hipoteza zavrnjena, tako da se oba medsebojno izključujeta.

Raven pomembnosti

To je ukrep za napako, ki jo je mogoče izvesti pri preizkusu hipoteze. Opredeljena je kot verjetnost zavrnitve ničelne hipoteze, saj je resnična. Običajno je označen z grško črko α:

α = p (zavrne h₀ Ko je res)

Vrednosti, ki se običajno uporabljajo za α, so 0.01, 0.05 in 0.10; je druga najpogostejša uporaba. Enakovredno 1%, 5% in 10% verjetnost, da bo storil napake, ko zavrnete h₀, Vsekakor pa je nižja stopnja pomena, bolj zanesljiv je rezultat testa.

Vrednost alfa (α) lahko razumemo kot odstotni delež območja desnega repa (ali levega), v normalni porazdelitvi (μ = 0 in σ = 1) in te vrednosti se vedno pojavijo pri z = 2,33 za α = 0.01; pri z = 1,65 za α = 1,65 in pri z = 1,29 za α = 0,1.

Koraki za izvedbo testa hipoteze

Korak 1

Določite ničelne in alternativne hipoteze. Nična hipoteza določa, da je preučevalni parameter, imenovan θ, enak referenčni vrednosti, označen kot θ₀:

H₀: θ = θ₀

Na primer, če se učinki zdravila raziskujejo na določeno značilnost populacije laboratorijskih miši₀.

Za simboliziranje ničelne hipoteze se na drugi strani vedno uporablja znak enakosti, alternativna hipoteza uporablja enega od simbolov ali ≠.

V primeru zdravila alternativna hipoteza ugotovi, da spojina nekaj vpliva na zadevno značilnost. Zato je to večje, nižje ali preprosto drugačno od referenčne vrednosti θ₀.

Vam lahko služi: faktorski zapis: koncept, primeri in vaje

2. korak

Izberite ustrezno raven pomembnosti, ki se običajno vzpostavi na 5 %, kot je bilo že navedeno.

Korak 3

Določite populacijo in iz njega izvlečite vzorec ali vzorce, katerih analiza bo služila za kontrast hipotez in določila sprejemanje ali zavrnitev ničelne hipoteze.

4. korak

Izberite in izračunajte vrednost preskusne statistike za zbrane podatke, iz katerih se pridobijo potrebni dokazi za sprejemanje odločitve za sprejemanje ali zavrnitev ničelne hipoteze. Izbira statistike preskusa je odvisna od izbranega parametra: srednje, odstopanja, deleža ali drugega.

Preskusna statistika dobimo s pretvorbo vzorčnega parametra v oceno Z, študenta, r Pearsona ali Chi Square statistiko, v skladu z izbrano eksperimentalno zasnovo. Za to obstajajo formule.

Običajno, če je parameter populacije povprečni μ, je „x bar“ povprečna vrednost, znana je standardni odklon σ in velikost vzorca je n> 30, preskusna statistika z_C Izračuna se z oceno Z:

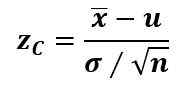
In ko n < 30, pero σ es desconocida, se usa la t de Student.

5. korak

Vzpostavite merila za sprejemanje ali zavrnitev ničelne hipoteze, ki jih je mogoče izvesti z dvema postopkoma:

• Skozi p vrednosti.
• V primerjavi s kritičnimi vrednostmi.

P vrednosti so enakovredne verjetnosti, da dosežejo najdene rezultate, saj je ničelna hipoteza resnična. Če so te vrednosti majhne, ​​je ničelna hipoteza zavrnjena, če jih ni, je sprejeta. V vsakem primeru vrednosti P ne predstavljajo dokazov, da je alternativna hipoteza resnična.

Upoštevati je treba, da je v testu hipoteze mogoče narediti dve vrsti napak:

• Napaka tipa I: Zavrni h₀ Ko je res. Njegova verjetnost je α in je enakovredna stopnji dokaznega pomena.
• Napaka tipa II: Sprejmi h₀ Ko je dejansko napačno. Njegova verjetnost je označena kot β.

Lahko vam služi: kakšen je odnos med območjem Rhombusa in pravokotnikom?

6. korak

Se odločite, da sprejmete ali zavrnete ničelno hipotezo. Če se vrednosti P uporabijo, ko je P < α, se rechaza H₀ In h je sprejet₁, In drugače je h sprejet₀. Nabor vrednosti P < α se conoce como kritična regija. Če je statistika v tem intervalu, je H zavrnjen₀.

Podobno je v skladu z izbranim parametrom prebivalstva izbrana kritična vrednost. Če je to povprečje, nadaljujte na naslednji način:

• Test repa: θ < θ₀ ali θ> θ₀
• Dva repa test: | θ | < θ₀

Rešen primer

Stroj izdeluje vijake, katerih nominalna vrednost mora biti dolga 800 milimetrov, s standardnim odklonom 5%.

Izvede se naključni vzorec, torej v različnih dneh proizvodnje, ki znaša približno 40 vijakov. Ko se izračuna povprečna dolžina vzorca, dobimo vrednost 790 milimetra.

Ugotovite, ali je povprečna dolžina v toleranci s stopnjami pomembnosti 1%, 5% in 10%.

Rešitev

Prva je izračunati povprečno statistiko testa, ki je v tem primeru odstopanje razdeljenega povprečja med standardno napako populacije:

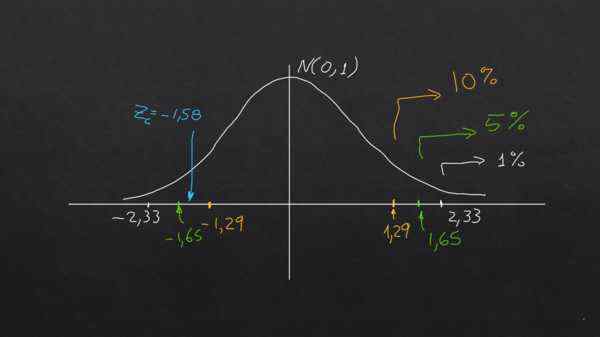
ZC = (790 - 800) / (40 / √40) = -1,58

Kjer je bilo upoštevano, da 5 -odstotni standardni odklon ustreza 40 od ​​800.

Nična hipoteza je, da je povprečni vzorec znotraj tolerance, ki je dovoljena do zahtevane ravni pomembnosti, pod pogojem, da | ZC | je manjša od tipizirane vrednosti | zt |, sicer je ničelna hipoteza zavrnjena.

Za 1% in 5% pomen je izpolnjena ničelna hipoteza, saj | ZC | < 2,33 y |Zc| < 1,65 respectivamente.

Vendar se za 10% pomen zgodi, da | ZC | > 1.29. To pomeni, da na tej stopnji pomembne hipoteze ni izpolnjena.

Naslednji graf pojasni zaključek:

Graf prikazuje, odvisno od stopnje pomembnosti, ki je potrebna enaka hipoteza, je mogoče sprejeti ali zavrniti z istimi podatki. Vir: f. Zapata.