Običajna porazdelitev formule, značilnosti, primer, vadba

The normalna porazdelitev o Gaussova porazdelitev je porazdelitev verjetnosti v neprekinjeni spremenljivki, pri kateri je funkcija gostote verjetnosti opisana z eksponentno funkcijo kvadratnega in negativnega argumenta, kar ima za posledico razrezano obliko.

Normalno ime porazdelitve izvira iz dejstva, da je ta porazdelitev tista, ki se uporablja za največje število situacij, v katerih je v določeni skupini ali populaciji vključena nekaj neprekinjene naključne spremenljivke.

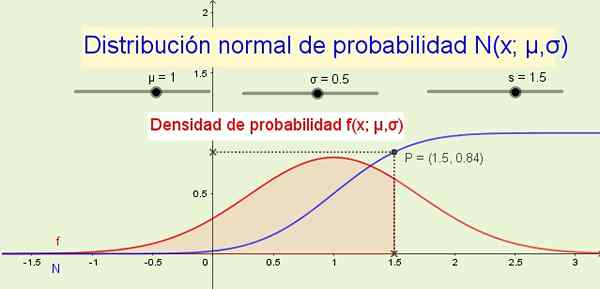
Slika 1. Normalna porazdelitev n (x; μ, σ) in njegova verjetnostna gostota f (s; μ, σ). (Lastna izdelava)

Kot primeri, pri katerih se uporablja normalna porazdelitev: višina moških ali žensk, različice v obsegu neke fizične razsežnosti ali merljivih psiholoških ali socioloških značilnosti, kot so intelektualni količnik ali potrošniške navade določenega izdelka.

Po drugi strani pa se imenuje Gaussova distribucija ali Gaussov Bell, ker je ta nemški matematični genij zaslužen za njegovo odkritje za uporabo, ki jo je dal za opis statistične napake astronomskih meritev leta 1800.

Vendar se trdi, da je to statistično porazdelitev že prej objavil še en velik matematik francoskega porekla, prav tako Abraham de Movre, leta 1733.

[TOC]

Formula

Do normalne porazdelitvene funkcije v neprekinjeni spremenljivki x, S parametri μ in σ Označuje ga:

N (x; μ, σ)

In izrecno je napisano tako:

N (x; μ, σ) = ∫_-∞^x f (s; μ, σ) ds

kje f (u; μ, σ) To je funkcija gostote verjetnosti:

f (s; μ, σ) = (1/(σ√ (2π)) exp ( - s - s²/(2σ²)

Konstanta, ki pomnoži eksponentno funkcijo v funkciji gostote verjetnosti, se imenuje normalizacijska konstanta in je bila izbrana tako, da:

N (+∞, μ, σ) = 1

Prejšnji izraz zagotavlja verjetnost, da je naključna spremenljivka x biti med -∞ in +∞ bodisi 1, to je 100 -odstotna verjetnost.

Parameter μ Je aritmetična srednja vrednost neprekinjene naključne spremenljivke x in σ Standardni odklon ali kvadratni koren variance iste spremenljivke. V primeru, da μ = 0 in σ = 1 Imate običajno standardno ali normalno porazdelitev porazdelitve: 

N (x; μ = 0, σ = 1)

Običajne značilnosti porazdelitve

1- Če naključna statistična spremenljivka sledi normalni porazdelitvi gostote verjetnosti f (s; μ, σ), Večina podatkov je razvrščena po povprečni vrednosti μ In so razpršeni okoli njih, tako da so tik nad podatki med μ - σ in μ + σ. 

Vam lahko služi: absolutna frekvenca: formula, izračun, porazdelitev, primer

2- standardni odklon σ Vedno je pozitivno.

3- oblika funkcije gostote F Spominja na to, da je zvonec, zato se ta funkcija pogosto imenuje Gaussian Bell ali Gaussova funkcija. 

4- V Gaussovi distribuciji povprečje, mediana in moda sovpadajo.

5- Točke pregibanja funkcije gostote verjetnosti najdemo natančno v μ - σ in μ + σ.

6- Funkcija F je simetrična glede na osi, ki prehaja po povprečni vrednosti μ In imate nič asimptotično za x ⟶ +∞ in x ⟶ -∞.

7- višja vrednost σ Večja disperzija, hrup ali distanciranje podatkov okoli povprečne vrednosti. To pomeni za večje σ Oblika zvona je bolj odprta. Namesto tega σ Majhna kaže, da je kocka plavala na povprečje in oblika zvona je bolj zaprta ali usmerjena.

8- Funkcija distribucije N (x; μ, σ) kaže na verjetnost, da je naključna spremenljivka manjša ali enaka x. Na primer na sliki 1 (zgoraj) verjetnost p, da spremenljivka x je manjša ali enaka 1.5 je 84% in ustreza območju pod funkcijo gostote verjetnosti f (x; μ, σ) Od -∞ do x.

Intervali zaupanja

9- Če podatki sledijo običajni porazdelitvi, potem je 68,26% med njimi μ - σ in μ + σ.

10- 95,44% podatkov, ki sledijo običajni porazdelitvi, so med μ - 2σ in μ + 2σ.

11- 99,74% podatkov, ki sledijo običajni porazdelitvi, so med μ - 3σ in μ + 3σ.

12- Če naključna spremenljivka x Sledite distribuciji N (x; μ, σ), Nato spremenljivka

Z = (x - μ) / σ  Sledite standardni normalni porazdelitvi  N (z; 0,1).

Sprememba spremenljivke x do z Imenuje se standardizacija ali tipkanje in je zelo uporabna v času uporabe standardnih tabel za distribucijo na podatkih, ki sledijo običajni nestandardni distribuciji.

Običajne aplikacije za distribucijo

Za uporabo običajne porazdelitve je treba skozi izračun integrala gostote verjetnosti, ki z analitičnega vidika ni enostavno in ni vedno na voljo računalniškega programa, ki omogoča svoj numerični izračun. V ta namen so uporabljene standardne ali tipizirane vrednosti tabele, kar ni nič drugega kot običajna porazdelitev v primeru μ = 0 in σ = 1.

Vam lahko služi: kombinirane operacije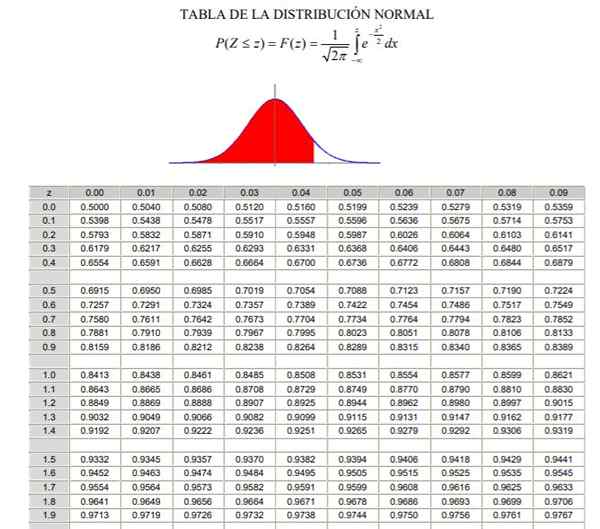Običajna tabela distribucije Tipizirana (del 1/2) 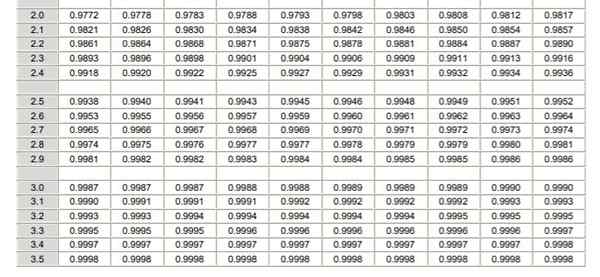Običajna tabela distribucije Tipizirana (del 2/2)

Treba je opozoriti, da te tabele ne vključujejo negativnih vrednosti. Vendar pa lahko s pomočjo lastnosti simetrije funkcije Gaussove gostote verjetnosti dobimo ustrezne vrednosti. V rešeni vaji, prikazani spodaj, je v teh primerih prikazana uporaba tabele.

Primer

Predpostavimo, da imate naključni niz podatkov X, ki sledijo normalni povprečni porazdelitvi 10 in standardnega odklona 2. Zahteva se, da najdete verjetnost, da:

a) Naključna spremenljivka x je manjša ali enaka 8.

b) je manjši ali enak 10.

c) da je spremenljivka x pod 12.

d) verjetnost, da je vrednost x med 8 in 12.

Rešitev:

a) Če želite odgovoriti na prvo vprašanje, morate izračunati:

N (x; μ, σ)

Z x = 8, μ = 10 in σ = 2. Zavedamo se, da je integral, ki v osnovnih funkcijah nima analitične rešitve, vendar je rešitev izražena v skladu s funkcijo napake Erf (x).

Po drugi strani pa obstaja možnost reševanja integrala na številčen način, to je tisto, kar mnogi kalkulatorji, preglednice in računalniški programi, kot je Geogebra, do. Naslednja slika prikazuje numerično rešitev, ki ustreza prvemu primeru:

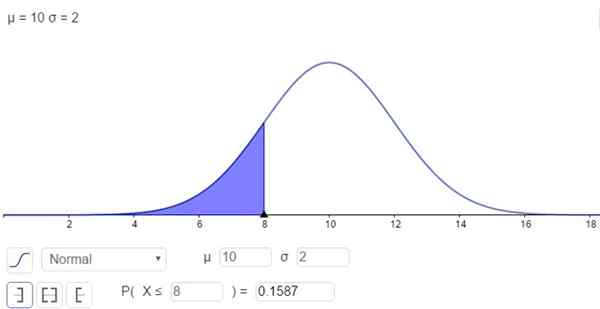Slika 2. Gostota verjetnosti f (x; μ, σ). Zasenčeno območje predstavlja P (x ≤ 8). (Lastna izdelava)

In odgovor je, da je verjetnost, da je X pod 8,:

P (x ≤ 8) = n (x = 8; μ = 10, σ = 2) = 0,1587

b) V tem primeru gre za iskanje verjetnosti, da je naključna spremenljivka x pod povprečjem, da je v tem primeru vredno 10. Odgovor ne zahteva nobenega izračuna, saj vemo, da je polovica podatkov pod povprečjem, druga polovica pa nad povprečjem. Zato je odgovor:

P (x ≤ 10) = n (x = 10; μ = 10, σ = 2) = 0,5

c) Če želite odgovoriti na to vprašanje N (x = 12; μ = 10, σ = 2), kar je mogoče storiti s kalkulatorjem, ki ima statistične funkcije ali s programsko opremo, kot je geogebra:

Vam lahko služi: delitve 8: Kaj so in lahka razlaga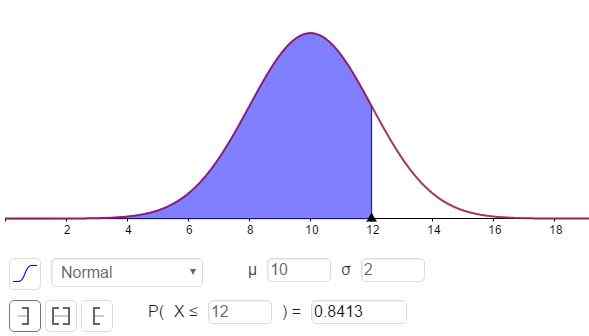Slika 3. Gostota verjetnosti f (x; μ, σ). Zasenčeno območje predstavlja P (x ≤ 12). (Lastna izdelava)

Odziv na del C je razviden na sliki 3 in je:

P (x ≤ 12) = n (x = 12; μ = 10, σ = 2) = 0,8413.

D) Da bi našli verjetnost, da je naključna spremenljivka x med 8 in 12, lahko uporabimo rezultate delov A in C na naslednji način:

P (8 ≤ x ≤ 12) = p (x ≤ 12) - p (x ≤ 8) = 0,8413 - 0,1587 = 0,6826 = 68,26.

Vaja rešena

Povprečna cena delnic podjetja znaša 25 dolarjev s standardnim odklonom 4 USD. Določite verjetnost, da:

a) Akcija ima stroške manj kot 20 dolarjev.

b) ki ima stroške večje od 30 USD.

c) Cena je med 20 in 30 USD.

Za iskanje odgovorov uporabite običajne tabele za distribucijo.

Rešitev:

Da bi uporabili tabele, se je treba premakniti na normalizirano ali tipizirano spremenljivko:

20 USD v standardizirani spremenljivki je enako Z = (20 USD - 25 dolarjev) / $ 4 = -5/4 = -1,25 in 

30 USD v standardizirani spremenljivki je enako Z = (30 USD - 25 dolarjev) / $ 4 = +5/4 = +1.25.

A) 20 USD je v standardizirani spremenljivki enakovreden -1,25, vendar tabela nima negativnih vrednosti, zato damo vrednost +1,25, ki prikazuje vrednost 0,8944.

Če se ta vrednost odšteje 0,5 Rezultat bo območje med 0 in 1,25, ki je mimogrede enaka (po simetriji) na območje med -1.25 in 0. Rezultat odštevanja je 0,8944 - 0,5 = 0,3944, kar je območje med -1.25 in 0.

Toda območje interesi od -∞ do -1,25, ki bo 0,5 -0,3944 = 0,1056. Zato je ugotovljeno, da je verjetnost, da je dejanje pod 20 USD, 10,56%.

b) 30 $ v tipificirani spremenljivki Z je 1,25. Za to vrednost v tabeli se prikaže številka 0,8944, ki ustreza območju od -–∞ do +1.25. Območje med +1.25 y +∞ je (1 - 0,8944) = 0,1056. Z drugimi besedami, verjetnost, da dejanje stane več kot 30 dolarjev, znaša 10,56%.

c) Verjetnost, da ima dejanje strošek med 20 in 30 USD, bo izračunana na naslednji način:

100% -10,56% - 10,56% = 78,88%

Reference

1. Statistika in verjetnost. Normalna porazdelitev. Pridobljeno iz: ProjectOdescartes.org
2. Geogebra. Klasična geogebra, izračun verjetnosti. Okreval od Geogebre.org
3. MathWorks. Gaussova porazdelitev. Okrevano od: je.MathWorks.com
4. Mendenhall, w. 1981. Statistični podatki za upravo in ekonomijo. 3. mesto. izdaja. Uredniška skupina Iberoamerica.
5. Stat Trek. Naučite se statistike. Poissonova distribucija. Obnovljeno od: stattrek.com,
6. Triola, m. 2012. Osnovna statistika. 11. Ed. Pearson Education.
7. Univerza v Vigo. Glavne neprekinjene distribucije. Okrevano od: anapg.spletna mesta.Uvigo.je
8. Wikipedija. Normalna porazdelitev. Okrevano od: je.Wikipedija.org