Lastnosti delnih derivatov, izračun, vaje

The delni derivati funkcije z več neodvisnimi spremenljivkami so tiste, ki jih dosežemo z običajnim derivatom v eni od spremenljivk, druge.

Delni derivat v eni od spremenljivk določa, kako se funkcija spreminja na vsaki točki, na enoto spremembe zadevne spremenljivke. 

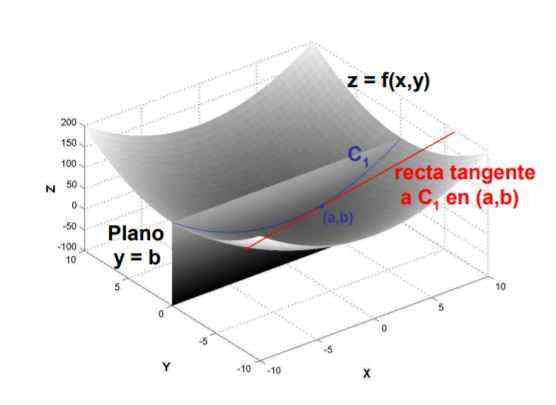Slika 1. Nagib tangentne črte do krivulje, ki jo tvori presečišče ravnine y = b s površino f (x, y) v točki (a, b), je delni derivat F glede na x, ocenjeno na tej točki. Vir: UPM.je

Zaradi svoje definicije se delni derivat izračuna z matematično mejo količnika med spreminjanjem funkcije in spreminjanjem spremenljivke glede na izpeljano, ko se sprememba slednjega nagiba na ničlo.

Predpostavimo, da je primer funkcije F Odvisno je od spremenljivk x in in, to pomeni za vsak par (X, y) A je dodeljen z: 

F: (x, y) → z .

Delni derivat funkcije z = f (x, y), iz spoštovanja do x je opredeljen kot:

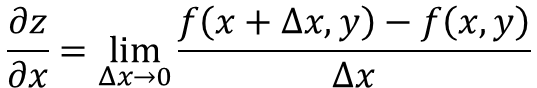
Zdaj obstaja več načinov za označevanje delnega derivata funkcije, na primer:

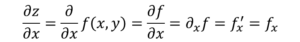
Razlika z navadnim derivatom v smislu zapisovanja je v tem, da d izpeljave se spremeni v simbol ∂, znan kot "Jacobi D".

[TOC]

Lastnosti delnih derivatov

Delni derivat funkcije več spremenljivk glede na eno od njih je navaden derivat v omenjeni spremenljivki in upoštevanje ostalih kot fiksne ali konstantne. Za iskanje delnega izvedenega finančnega instrumenta se lahko uporabijo pravila izpeljave običajnih derivatov.

Pod glavne lastnosti:

Vam lahko služi: skupni dejavnik za razvrščanje izrazov: primeri, vaje

Kontinuiteta

Če je funkcija f (x, y) ima delne derivate v x in in na točki (Xo, jaz) potem lahko rečemo, da je funkcija v tistem trenutku neprekinjena.

Pravilo verige

Funkcija f (x, y) Z neprekinjenimi delnimi derivati ​​v x in in, kar je odvisno od parametra t skozi x = x (t) in y = y (t), Ima navaden derivat glede na spremenljivko t, ki se izračuna s pravilom verige:

d_t Z = ∂_xz d_tx + ∂_inz d_tin

Lastnost zapiranja ali zaklepanja

Delni derivat glede na eno od spremenljivk funkcije F od dveh ali več spremenljivk (X, y, ...), To je še ena funkcija g Na primer v istih spremenljivkah: 

G (x, y, ...) = ∂_in f (x, y, ...)

To pomeni, da je delna izpeljava operacija, ki gre od rⁿ a rⁿ. V tem smislu je rečeno, da gre za zaprto delovanje.

Zaporedni delni derivati

Zaporedni delni derivati ​​funkcije več spremenljivk je mogoče določiti, kar povzroči nove funkcije v istih neodvisnih spremenljivkah.

Biti funkcija f (x, y). Naslednje zaporedne derivate je mogoče opredeliti:

F_Xx = ∂_xF ;  F_Yy = ∂_YyF ; F_Xy = ∂_XyF in F_Yx = ∂_YxF

Zadnja dva sta znana kot Mešani derivati Ker vključujeta dve različni neodvisni spremenljivki.

Schwarzov teorem

Biti funkcija f (x, y), definirano tako, da so njeni delni derivati ​​neprekinjene funkcije v odprti podskupini R².

Torej, za vsak pare (X, y) Da pripadajo omenjeni podskupini, so mešani derivati ​​enaki:

∂_XyF = ∂_YxF

Prejšnja izjava je znana kot Schwarzov teorem.

Kako se izračunajo delni derivati?

Delni derivati ​​se izračunajo podobno kot običajne finančne derivate v eni neodvisni spremenljivki. Ko se delna derivat funkcije več spremenljivk sprejme glede na eno od njih, se druge spremenljivke vzamejo kot konstante.

Vam lahko služi: polovica od 15

Spodaj je več primerov:

Primer 1

Biti funkcija:

f (x, y) = -3x² + 2 (in - 3)²

Zahteva se izračunati prvi delni derivat glede na to x in prvi delni derivat glede na in.

Postopek

Za izračun delnega F iz spoštovanja do x, Je zaseden in kot konstantno:

∂_xF = ∂_x(-3x² + 2 (in - 3)² ) = ∂_x(-3x² )+ ∂_x(2 (in - 3)² ) = -3 ∂_x(x²) + 0 = -6x.

In po drugi strani za izračun derivata glede na to in Je zaseden x kot konstantno:

∂_inF = ∂_in(-3x² + 2 (in - 3)² ) = ∂_in(-3x² )+ ∂_in(2 (in - 3)² ) = 0 + 2 · 2 (y - 3) = 4y - 12.

Primer 2

Določite delne derivate drugega reda:  ∂_Xxf, ∂_Yyf, ∂_YxF in ∂_XyF Za isto funkcijo F Primer 1.

Postopek

V tem primeru, kot se prvi delni derivat že izračuna v x in in (Glej primer 1):

∂_XxF = ∂_x(∂_xf) = ∂_x(-6x) = -6

∂_YyF = ∂_in(∂_inf) = ∂_in(4y - 12) = 4

∂_YxF = ∂_in(∂_xf) = ∂_in(-6x) = 0

∂_XyF = ∂_x(∂_inf) = ∂_x(4y - 12) = 0

Opazimo, da ∂_YxF = ∂_XyF, s tem izpolnjevanje Schwarzovega teorema, od funkcije F in njegovi prvi delni derivati ​​so vse neprekinjene funkcije v R².

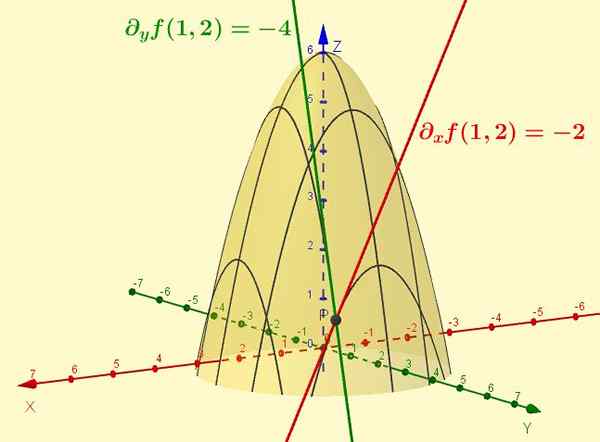
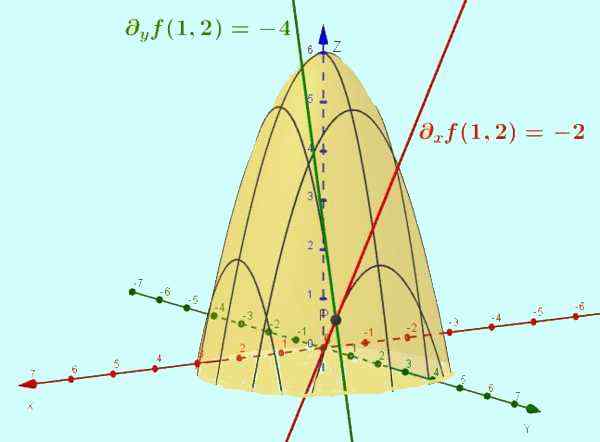Slika 2. Funkcija z = f (x, y) = -x2 - y2 + 6 je površina, prikazana na sliki. Delni derivat glede na X je naklon tangentne črte krivulje, ki je posledica presečišča omenjene površine z ravnino y = ctte (poseben primer je prikazan y = 2). Podobno je del F glede in je naklon tangenta do križišča z x = 1 v točki (1, 2, 1).

Rešene vaje

Vaja 1

Biti funkcija:

Vam lahko služi: kvadratni nasledniki: primeri, pravilo in vaje rešene

f (x, y) = -x² - in² + 6

Poiščite funkcije G (x, y) = ∂_xF  in H (x, y) = ∂_inF.

Rešitev

Delni derivat F iz spoštovanja do x, za katero je spremenljivka in Postane konstantno:

G (x, y) = - 2x

Podobno je delni derivat g iz spoštovanja do in, delati x konstanta, ki ima za posledico funkcijo h:

H (x, y) = -2y

Vaja 2 

Ocenite za točko (1, 2) funkcije f (x, y) in G (x, y) vaje 1. Razlaga rezultate.

Rešitev

Vrednosti se nadomestijo x = 1 in y = 2 pridobivanje:

f (1,2) = -(1)² -(2)² + 6 = -5 + 6 = 1

To je vrednost, ki prevzame funkcijo f, ko je na tej točki ocenjena.

Funkcija f (x, y) Je dvodimenzionalna površina in koordinata z = f (x, y) To je višina funkcije za vsak par (X, y). Ko je par vzet (1.2), Višina površine f (x, y) je Z = 1.

Funkcija G (x, y) = - 2x predstavlja ravnino v tridimenzionalnem prostoru, katerega enačba je Z = -2x O dobro -2x + 0 in -z = 0.

Omenjeno letalo je pravokotno na ravnino Xz In pojdi skozi točko (0, 0, 0). Ko je ocenjen v x = 1 in y = 2 tako Z = -2. Upoštevajte, da vrednost z = g (x, y) Je neodvisna od vrednosti, dodeljene spremenljivki in.

Po drugi strani pa, če se površina seka f (x, y) Z letalom y = c, z c konstantno, imate krivuljo v ravnini ZX: z = -x² - c² + 6.

V tem primeru izpeljan od z iz spoštovanja do x sovpada z delnim derivatom f (x, y) iz spoštovanja do x: d_x Z = ∂_xF .

Pri ocenjevanju v paru (x = 1, y = 2) Delni derivat v tem trenutku ∂_xF (1.2) Razlaga se kot naklon črte tangenta do krivulje z = -x² + 2 na točki (x = 1, y = 2) In vrednost tega pobočja je -2.

Reference

1. Ayres, f. 2000. Izračun. 5ed. MC Graw Hill.
2. Delni derivati ​​funkcije v več spremenljivkah. Okrevano od: stavba.UPM.je.
3. Leithold, l. 1992. Izračun z analitično geometrijo. Harla, s.Do.
4. Purcell, e. J., Varberg, d., & Rigdon, s. In. (2007). Izračun. Mehika: Pearson Education.
5. Gorostizaga J. C. Delni derivati. Okreval od: ehu.Eus
6. Wikipedija. Delni derivat. Okrevano od: je.Wikipedija.com.