Implicitni derivati, kako so rešeni in rešeni vaje

The implicitni derivati To so orodja, ki se uporabljajo v tehniki diferenciacije, ki se uporabljajo za funkcije. Uporabljajo se, kadar to po rednih metodah ni mogoče, izvedejo odmik odvisne spremenljivke. Ta odmik se opravi na podlagi neodvisne spremenljivke.

Na primer v izrazu 3xy³ - 2y + xy² = xy, ne morete dobiti izraza, ki definira "y", odvisno od "x". Tako da, ko lahko dobimo diferencialni izraz dy/dx.

[TOC]

Kako se rešijo implicitni derivati?

Za reševanje posledic temelji na implicitnem izrazu. Na primer: 3xy³ - 2y + xy² - Xy = 0. To je že jasno očiščeno, vendar to storiti ni nujen pogoj za pridobitev izpeljanka Y glede x. Nato se vsak od elementov izpelje v zvezi s pravilom verige za mešane funkcije:

3xy³ Sestavljen je iz dveh spremenljivk, torej d (3xy³) Obravnava se bo kot derivat izdelka funkcij.

D (3xy³)/dx = 3y³ + 3y².(3x) in '= 3y³ + 9xy² in

Kjer je element in 'znan kot "in bratranec”In Dy/dx predstavlja

-2y izhaja v skladu z zakonom k.U = k.Ali

D (-2y) = -2 in '

Xy² Predpostavimo še en diferencial, sestavljen iz produkta funkcij

D (xy²) = y² + 2xy in '

-XY je homologna pot

d (-xy) = -y -x in '

Nadomeščeni so v enakosti, vedoč, da je ničle derivat nič.

3y³ + 9xy² in ' - 2 in' + in² + 2xy in ' - y - x in' = 0

Elementi, ki imajo izraz in 'so združeni na eni strani enakosti

Vam lahko služi: colinealni vektorji

3y³ + in² - y = -9xy² in ' + 2 in' + x in '

Skupni dejavnik in 'v desnem članu enakosti se izvleče

3y³ + in² - y = y '(-9xy² + x + 2)

Končno izraz, ki se pomnoži in '. S tem pridobivanje izraza, ki ustreza implicitnemu derivatu Y glede x.

in '= dy/dx = (3y³ + in² - y)/(-9xy² + x + 2)

Pravilo verige

V implicitni izpeljavi se pravilo verige vedno spoštuje. Vsi diferencialni izrazi bodo podani glede na neodvisno spremenljivko x. Tako da mora vsaka spremenljivka θ, ki se razlikuje od x.

Ta izraz se bo pojavil le v prvi stopnji ali z eksponentom, ki je enaka 1. Ta kakovost je popolnoma jasno po tradicionalnih metodah faktorizacije. Tako da postane mogoče dobiti izraz, ki določa diferencialno dθ/dx.

V verižnem pravilu je prikazana progresivna narava diferenciacije ali izpeljanega procesa. Kjer bo treba za katero koli sestavljeno funkcijo f [g (x)] diferencialni izraz F

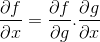
Operativno naročilo

V vsakem zakonu o formuli ali izpeljavi je treba upoštevati vrstni red spremenljivk. Merila, povezana z neodvisno spremenljivko, so spoštovana, ne da bi spremenili njegovo povezanost z odvisno spremenljivko.

Razmerje odvisne spremenljivke v času izpeljane je odvzeto.; Z izjemo, da se bo to štelo za drugo funkcijo, zato se uporabljajo merila verižnega pravila za mešane funkcije.

To je mogoče razviti v izrazih z več kot dvema spremenljivkama. Po istih načelih bodo vse razlike, ki se nanašajo na odvisne spremenljivke.

Vam lahko služi: kakšna je smernica? (Geometrija)

Grafično se obravnava enaka merila, ki definirajo izpeljan. Medtem ko je derivat naklon črte tangenta do krivulje v ravnini, preostali del diferencialov, ki pripadajo odvisnim spremenljivkam (dy/dz, dz/dx).

Implicitno funkcije

Govori se, da je funkcija implicitno definirana, če je lahko izraz y = f (x) predstavljen kot večkratna spremenljiva funkcija f (x, y) = 0, medtem ko je F definiran v ravnini r².

3xy³ - 2y + xy² = x in ga je mogoče zapisati v obliki 3xy³ - 2y + xy² - Xy = 0

Glede na nemogoče razložiti funkcijo y = f (x).

Zgodovina

Diferencialni računanje so začeli imenovati različni matematični raziskovalci, okoli sedemnajstega stoletja. Prvič je bil omenjen prek Newtona in Leibnizovega prispevka. Oba sta obravnavala diferencialni računanje z različnih vidikov, vendar sta se zbližala v svojih rezultatih.

Medtem ko se je Newton osredotočil na diferenciacijo kot hitrost ali hitrost variacije, je bil Leibniz pristop bolj geometrijski. Lahko rečemo, da je Newton napadel domneve, ki jih je zapustil Apollonius iz Pergea in Leibniza geometrijske ideje Fermata.

Implicitna izpeljava se pojavi takoj, ko razmislijo o diferencialnih in celovitih enačbah. Geometrijski koncept Leibniz so razširili na R³ in celo večdimenzionalni prostori.

Prijave

Implicitni derivati ​​se uporabljajo v različnih situacijah. So pogoste pri težavah z menjalnimi tečaji med sorodnimi spremenljivkami, kjer bodo spremenljivke, odvisno od občutka študije.

Imajo tudi zanimive geometrijske aplikacije, na primer v težavah z razmišljanji ali sencami, na figurah, katerih obliko je mogoče matematično modelirati.

Vam lahko služi: vzorčenje kvot: metoda, prednosti, slabosti, primeri

Pogosto uporabljajo na področju gospodarstva in inženiringa, pa tudi v različnih preiskavah naravnih pojavov in eksperimentalnih zgradb.

Rešene vaje

Vaja 1

Določite implicitni izraz, ki definira dy/dx

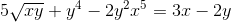
Vsak element se razlikuje od izraza

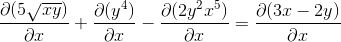
Vzpostavitev pravila verige v vsakem pristojnem primeru

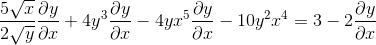
Razvrščanje na eni strani enakosti elementov, ki imajo dy/dx

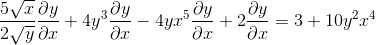
Je faktor z uporabo skupnega faktorja

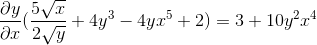
Se očisti z pridobivanjem iskanega izraza

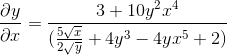
Vaja 2

Določite implicitni izraz, ki definira dy/dx

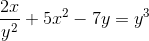
Izražanje derivatov za izvedbo

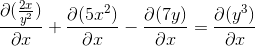
Implicitno izpeljava po pravilu verige

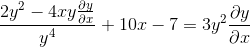
Faktor skupnih elementov

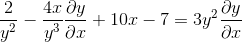
Razvrščanje izraza dy/dx na eni strani enakosti

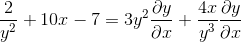
Skupni dejavnik diferencialnega elementa

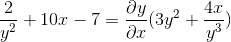
Očistimo in pridobimo iskani izraz

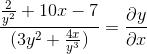
Reference

1. Izračun ene same spremenljivke. Ron Larson, Bruce H. Edwards. Cengage Learning, 10. november. 2008
2. Teorem implicitne funkcije: Zgodovina, teorija in aplikacije. Steven G. Krantz, Harold R. Parki. Springer Science & Business Media, 9. november. 2012
3. Multivariabilna analiza. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. december. 2010
4. Sistemska dinamika: modeliranje, simulacija in nadzor mehatronskih sistemov. Dean c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. marca. 2012
5. Calculus: matematika in modeliranje. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick VITRAY. Addison Wesley Longman, 1. januar. 1999