Razvrščeni podatkovni primeri in rešena vaja

The združeni podatki To so tisti, ki so razvrstili v kategorije ali razrede in kot merila njihova pogostost. To se naredi z namenom poenostavitve upravljanja velikih količin podatkov in vzpostavljanju njihovih trendov.

Ko so v teh razredih organizirani za svoje frekvence, podatki sestavljajo a Porazdelitev frekvence, iz katerih se informacije o uporabnosti pridobivajo z njegovimi značilnostmi.

Slika 1. Z združenimi podatki lahko sestavite grafiko in izračunate statistične parametre, ki opisujejo trende. Vir: Pixabay.

Nato bomo videli preprost primer združenih podatkov:

Recimo, da se izmeri stas 100 študentk, izbranih med vsemi osnovnimi fizikami univerze, in pridobljeni so naslednji rezultati:

Pridobljeni rezultati so bili razdeljeni v 5 razredov, ki se pojavijo v levem stolpcu.

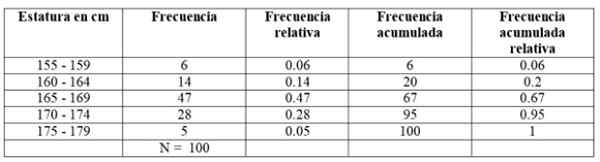
Prvi razred, med 155 in 159 cm, ima 6 učencev, drugi razred 160 - 164 cm ima 14 učencev, tretji razred od 165 do 169 cm je tisti z največjim številom članov: 47. Nato sledite razredu 170-174 cm z 28 študenti in končno tistega od 175 do 179 cm s samo 5.

Število članov vsakega razreda je natančno frekvenca tudi Absolutna bremenitev In z dodajanjem vseh se dobijo skupni podatki, kar je v tem primeru 100.

[TOC]

Karakteristike frekvence

Frekvenca

Kot smo videli, je frekvenca, kolikokrat se ponavlja dejstvo. In za olajšanje izračunov distribucijskih lastnosti, kot sta povprečje in odstopanje, so določene naslednje količine:

-Nakopičena frekvenca: Dobimo ga z dodajanjem frekvence razreda s sprednjo nakopičeno frekvenco. Prva vse frekvence sovpada s tistim v zadevnem intervalu, zadnje pa je skupno število podatkov.

-Relativna frekvenca: Izračuna se z deljenjem absolutne frekvence vsakega razreda s skupnim številom podatkov. In če se pomnožite s 100.

Vam lahko služi: vektorske funkcije

-Nakopičena relativna frekvenca: To je vsota relativnih frekvenc vsakega razreda s prejšnjim nakopičenim. Zadnja od nakopičenih relativnih frekvenc mora biti enaka 1.

Za naš primer so frekvence takšne:

Meje

Kličejo se ekstremne vrednosti vsakega razreda ali intervala Omejitve razreda. Kot lahko vidimo, ima vsak razred spodnjo mejo in eno večjo. Na primer, prvi razred študije o stanju ima omejitev manj kot 155 cm in eno večjo od 159 cm.

Ta primer ima jasno določene omejitve, vendar je mogoče.

Meje

Višina je neprekinjena spremenljivka, zato je mogoče upoštevati, da se prvi razred dejansko začne leta 154.5 cm, saj z zaokrožitvijo te vrednosti na najbližje celo število dobimo 155 cm.

Ta razred zajema vse vrednosti do 159.5 cm, ker sta iz tega stanja zaokrožena na 160.0 cm. Stas 159.7 cm že spada v naslednji razred.

Resnične meje tega primera so v CM:

• 154.5 - 159.5
• 159.5 - 164.5
• 164.5 - 169.5
• 169.5 - 174.5
• 174.5 - 179.5

Amplituda

Širina razreda dobimo z odštevanjem meja. Za prvi interval našega primera imate 159.5 - 154.5 cm = 5 cm.

Bralec lahko preveri, da za druge intervale primera amplituda izhaja tudi iz 5 cm. Vendar je omembe vredno, da je mogoče distribucije zgraditi z intervali različne amplitude.

Lahko vam služi: pravilo T: značilnosti, tako da so primeri

Blagovna znamka razreda

To je srednja točka intervala in jo dobimo s povprečjem med zgornjo in spodnjo mejo.

Za naš primer je blagovna znamka prvega razreda (155 + 159)/2 = 157 cm. Bralec lahko preveri, ali so preostale blagovne znamke razreda: 162, 167, 172 in 177 cm.

Določitev blagovnih znamk je pomembna, saj je potrebna za iskanje aritmetične srednje vrednosti in odstopanja distribucije.

Ukrepi osrednje težnje in razpršenosti za združene podatke

Najbolj uporabljeni ukrepi osrednje težnje so povprečni, srednji in modni in natančno opisujejo težnjo podatkov, ki jih je treba razvrstiti okoli določene osrednje vrednosti.

Polovica

Je eden glavnih ukrepov osrednje tendence. V združenih podatkih lahko aritmetično srednjo vrednost izračunamo po formuli:

 Kje:

-X je povprečje

-F_Yo je frekvenca razreda

-m_Yo To je razredna znamka

-G je število razredov

-n je skupno število podatkov

Mediana

Za mediano morate prepoznati interval, kjer se nahaja opazovanje n/2. V našem primeru je to opazovanje številka 50, ker je skupno 100 podatkov. To opazovanje je v intervalu 165-169 cm.

Potem morate interpolavati, da najdete numerično vrednost, ki ustreza tistemu opazovanju, za katero se uporablja formula:

Kje:

-C = intervalna širina, kjer se nahaja mediana

-B_M = Spodnja meja intervala, ki mu pripada mediana

-F_m = količina opazovanj v srednjem intervalu

-N/2 = polovica celotnih podatkov

-F_Bm = Skupno število opazovanj pred srednjim intervalom

Moda

Za modo je identificiran modalni razred, ki vsebuje večino opazovanj, katerih blagovna znamka je znana.

Vam lahko služi: šesterokotna piramida

Odstopanje in standardni odklon

Variance in standardni odklon sta disperzijski ukrepi. Če označujemo odstopanje s S² In do standardnega odklona, ​​ki je kvadratni koren variance kot S, za združene podatke bomo imeli:

In

Vaja rešena

Za porazdelitev stasa študentov, predlaganih na začetku, izračunajte vrednosti:

a) povprečje

b) medij

c) moda

d) odstopanje in standardni odklon.

Slika 2. Ko gre za številne vrednosti, na primer stature velike skupine študentov, je zaželeno, da podatke razvrstimo v razrede. Vir: Pixabay.

Rešitev

Izdelajmo naslednjo tabelo, da olajšamo izračune:

Skozi izraz za povprečno skupino, razvrščeno zgoraj:

Zamenjava vrednosti in neposredno izvajanje vsote:

X = (6 x 157 + 14 x 162 + 47 x 167 + 28 x 172+ 5 x 177) /100 cm =

= 167.6 cm

Rešitev b

Interval, ki mu pripada mediana, je 165-169 cm, ker je interval najpogosteje.

Popredelimo vsako od teh vrednosti v primeru s pomočjo tabele 2:

C = 5 cm (glejte razdelek Amplitude)

B_M = 164.5 cm

F_m = 47

N/2 = 100/2 = 50

F_Bm = 20

Zamenjava v formuli:

Rešitev c

Interval, ki ga vsebuje večina opazovanj, je 165-169 cm, katerega blagovna znamka je 167 cm.

Rešitev d

Prejšnjo tabelo razširimo tako, da dodamo dva dodatna stolpca:

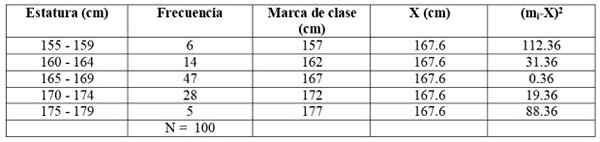
Uporabljamo formulo:

In razvijamo vsoto:

s² = (6 x 112.36 + 14 x 31.36 + 47 x 0.36 + 28 x 19.36 + 5 x 88.36) / 99 = = 21.35 cm²

Zato:

S = √21.35 cm² = 4.6 cm

Reference

1. Berenson, m. 1985. Statistični podatki za upravo in ekonomijo. Interameriški s.Do.
2. Canavos, g. 1988. Verjetnost in statistika: aplikacije in metode. McGraw Hill.
3. Devore, j. 2012. Verjetnost in statistika za inženirstvo in znanost. 8. Izdaja. Cengage.
4. Levin, r. 1988. Statistika za skrbnike. 2. mesto. Izdaja. Dvorana Prentice.
5. Spiegel, m. 2009. Statistika. Serija Schaum. 4 ta. Izdaja. McGraw Hill.
6. Walpole, r. 2007. Verjetnost in statistika za inženirstvo in znanost. Pearson.