U -test od Manna - Whitney Kaj je in kadar velja, izvedba, primer

The U -test od Manna - Whitney Uporablja se za primerjavo dveh neodvisnih vzorcev, kadar imata malo podatkov ali ne sledijo običajni distribuciji. Na ta način velja za test ni parametrično, Za razliko od vašega kolega Študent t test, ki se uporablja, kadar je vzorec dovolj velik in sledi normalni porazdelitvi.

Frank Wilcoxon ga predlaga prvič leta 1945 za vzorce enakih velikosti, dve leti pozneje pa sta ga Henry Mann in D razširila v primeru vzorcev različnih velikosti. R. Whitney.

Slika 1. U -test Mann - Whitney se uporablja za primerjavo neodvisnih vzorcev. Vir: Pixabay.

Pogosto se test uporablja za preverjanje, ali obstaja povezava med kvalitativno spremenljivko in drugo kvantitativno.

Ilustrativni primer je, da vzamete nabor hipertenzivnih ljudi in izvlečete dve skupini, na katere se dnevni podatki o krvnem tlaku beležijo mesec dni.

Za eno skupino je zdravljenje A in drugo uporabljeno zdravljenje B. Tu je krvni tlak kvantitativna spremenljivka in vrsta zdravljenja je kvalitativna.

Želite vedeti, ali je mediana in ne povprečje izmerjenih vrednosti statistično enaka ali drugačna, da ugotovite, ali obstaja razlika med obema tretmajem. Za pridobitev odgovora se uporablja Wilcoxon ali U -test Mann - Whitney.

[TOC]

Problem pristop v u -testu Mann - Whitney

Drug primer, pri katerem je mogoče uporabiti test, je naslednji:

Recimo, da želite vedeti, ali se poraba brezalkoholnih pijač v dveh regijah države znatno razlikuje.

Eden od njih se imenuje regija A in druga regija B. Izvedena je zapis o litrih, ki jih porabijo tedensko v dveh vzorcih: eden od 10 ljudi za regijo A in drugi od 5 ljudi za regijo B.

Podatki so naslednji:

-Regija a: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12

-Regija b: 12,14, 11, 30, 10

Postavljeno je naslednje vprašanje:

Ali je poraba brezalkoholnih pijač (y) odvisna od regije (x)?

Kvalitativne spremenljivke v primerjavi s kvantitativnimi spremenljivkami

-Kvalitativna spremenljivka x: Regija

-Kvantitativna spremenljivka in: Plinasta poraba

Če je v obeh regijah porabljena količina porabljenih litrov, bo zaključek, da med obema spremenljivkama ni odvisnosti. Način, kako vedeti, je primerjati povprečni ali srednji trend za obe regiji.

Običajni primer

Če so podatki sledili normalni porazdelitvi, se dvigneta dve hipotezi: NULL H0 in H1 alternativa s primerjavo med sredstvi:

Vam lahko služi: pomembni izdelki

-H0: Med povprečjem obeh regij ni razlike.

-H1: Sredstva obeh regij so različna.

Primer brez običajne težnje

Nasprotno, če podatki ne sledijo običajni porazdelitvi ali pa je vzorec zelo majhen, namesto da bi primerjali povprečje, bi ga primerjali Mediana od obeh regij.

-H0: Med mediano obeh regij ni razlike.

-H1: Mediani obeh regij so različni.

Če mediani sovpadajo, potem je izpolnjena ničelna hipoteza: med porabo sode in regijo ni povezave.

In če se zgodi nasprotno, je alternativna hipoteza resnična: obstaja razmerje med porabo in regijo.

Je za te primere, ko je nakazan test U Mann - Whitney.

Vzorčni ali neparni vzorci

Naslednje pomembno vprašanje za odločitev, ali je uporabljen test U Manna Whitneyja, je, ali je število podatkov v obeh vzorcih enako, kar je enakovredno temu, da so hkrati.

Če sta dva vzorca seznanjena, bi veljala originalna različica Wilcoxon. Če pa ne, kot je primer primera, se uporabi spremenjeni Wilcoxonov test, ki je natančno Mann Whitney's U test.

Mann Whitney u Preskusne značilnosti

U -test Mann -Whitney neparametrični test, ki se uporablja za vzorce, ki ne sledijo običajni porazdelitvi ali z malo podatki. Ima naslednje značilnosti:

1.- Primerjajte mediane

2.- Dela na urejenih območjih

3.- Je manj močan, razumevanje po moči verjetnost zavrnitve ničelne hipoteze, ko je v resnici napačna.

Upoštevanje teh značilnosti se uporablja U -test Mann - Whitney, ko:

-Podatki so neodvisni

-Ne sledijo običajni porazdelitvi

-Hipoteza NULL H0 je sprejeta, če medij obeh vzorcev sovpada: Ma = MB

-Alternativna hipoteza H1 je sprejeta, če se medij od obeh vzorcev razlikuje: Ma ≠ MB

Mann formula - Whitney

Spremenljivka U je kontrastna stalnost, ki se uporablja v testu Mann - Whitney in je opredeljena:

U = min (UA, UB)

To pomeni, da je U najmanj vrednosti med UA in UB, ki se uporabljajo za vsako skupino. V našem primeru bi bilo to za vsako regijo: a o b.

Spremenljivke UA in UB so definirane in izračunane v skladu z naslednjo formulo:

Ua = nb + na (Na +1)/2 - ra

UB = NB + NB (NB +1)/2 - RB

Vam lahko služi: zmanjšanje podobnih izrazov

Tu so vrednosti NA in NB velikosti vzorcev, ki ustrezajo regijam A in B, na drugi strani Range Sums da bomo določili spodaj.

Koraki za uporabo testa

1.- Naročite vrednosti obeh vzorcev.

2.- Vsaki vrednosti dodelite območje naročila.

3.- Popravite obstoječe ligature v podatkih (ponavljajoče vrednosti).

4.- Izračunajte RA = vsota razponov vzorca a.

5.- Poiščite RB = vsota razponov vzorca B.

6.- Določite vrednost UA in UB v skladu s formulami, navedenimi v prejšnjem razdelku.

7.- Primerjajte UA in UB, manjši od obeh pa je dodeljen ali eksperimentalni statistiki (torej podatki) v primerjavi s teoretično ali normalno statistiko.

Praktična uporaba prijave

Zdaj uporabimo že omenjeno težavo, ki je bila prej vzgojena:

Regija A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12

Regija B: 12,14, 11, 30, 10

Glede na to, da so sredstva obeh vzorcev statistično enaka ali drugačna, nadaljujemo s sprejemanjem ali zavračanjem ničelne hipoteze: med spremenljivko in X ni povezave, torej poraba sode ni odvisna od regije:

H0: MA = MB

H1: ma ≠ mb

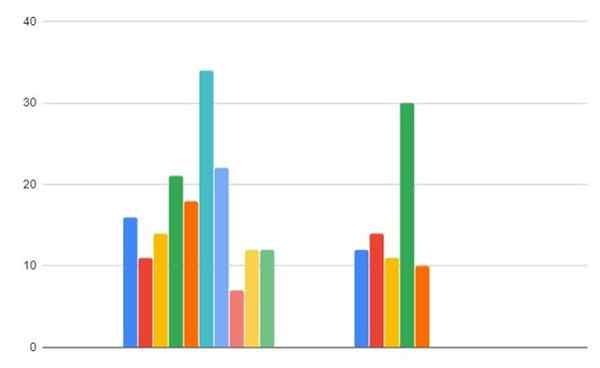Slika 2. Podatki o plinasti porabi v regijah A in B. Vir: f. Zapata.

- Korak 1

Podatke skupaj naročimo za dva vzorca, pri čemer naročimo vrednosti od najmanj do največjih:

Upoštevajte, da se vrednost 11 pojavi 2 -krat (enkrat v vsakem vzorcu). Prvotno ima položaje ali razpona 3 in 4, vendar ne preceniti ali podcenjevati eno ali drugo povprečno vrednost je izbrana kot razpon, to je 3,5.

Podobno se nadaljuje 12 vrednosti, ki se trikrat ponovi z razponi 5, 6 in 7.

No, vrednost 12 je dodeljena povprečni razpon 6 = (5+6+7)/3. In enako za vrednost 14, ki ima ligacijo (ki se pojavlja v obeh vzorcih) v položajih 8 in 9, dodeljen je povprečni razpon 8.5 = (8+9)/2.

- 2. korak

Podatki za regijo A in B se nato spet ločijo, zdaj pa so njihovi ustrezni razponi dodeljeni v drugi vrsti:

Regija a

Regija b

RB območja dobimo iz vsot elementov druge vrstice za vsak primer ali regijo.

Korak 3

Izračunane so ustrezne vrednosti UA in UB:

Ua = 10 × 5 + 10 (10 + 1)/2 - 86 = 19

UB = 10 × 5 + 5 (5 + 1)/2 -34 = 31

Eksperimentalna vrednost u = min (19, 31) = 19

4. korak

Teoretik naj bi sledil običajni porazdelitvi n s parametri, ki jih daje izključno velikost vzorcev:

Vam lahko služi: iracionalne številke: zgodovina, lastnosti, klasifikacija, primeri

N ((Na⋅nb) /2, √ [NB (Na + NB +1) /12])

Da bi primerjali spremenljivko ali eksperimentalno pridobljeno, je s teoretičnim potrebnim spreminjanjem spremenljive spremembe. Sega od spremenljivke ali eksperimentalne do njegove vrednosti tipizirano, ki se bo poklical Z, Da bi lahko primerjali s tipko, ki je navedena v normalni porazdelitvi.

Spremenljiva sprememba je naslednja:

Z = (u - na.Nb / 2) / √ [na. NB (NA + NB + 1) / 12] 

Treba je opozoriti, da so bili za spremembo spremenljivke uporabljeni parametri teoretične porazdelitve za U. Nato nova Z spremenljivka, ki je hibrid med teoretičnim in eksperimentalnim ali normalno porazdelitvijo, ki je tipizirala n (0,1).

Merila za primerjavo

Če z ≤ zα ⇒ Hipoteza NULL H0 je sprejeta

DA Z> Zα ⇒ Hipoteza NULL H0 je zavrnjena

Kritične vrednosti Zα, ki so tipizirane, so odvisne od potrebne stopnje zaupanja, na primer za raven zaupanja α = 0,95 = 95%, kar je najbolj običajno.

Za podatke, prikazane tukaj:

Z = (u - nb / 2) / √ [nb (na + nb + 1) / 12] = -0,73

Ki je pod kritično vrednostjo 1.96.

Potem je končni zaključek, da je ničelna hipoteza sprejeta:

V porabi sode med regijami A in B ni razlike.

Spletni kalkulatorji za u -test od Manna - Whitney

Obstajajo posebni programi za statistične izračune, vključno s SPSS in Minitab, vendar so ti programi plačani in njihova uporaba ni vedno preprosta. To je zato, ker dajejo toliko možnosti, da je njegova uporaba praktično rezervirana za statistične strokovnjake.

Na srečo obstaja več zelo natančnih, brezplačnih in preprostih spletnih programov, ki med drugim omogočajo teste U -Whitney U.

Ti programi so:

-Statistika družboslovja (Socscistatistics.com), ki ima tako u-Whitney u test kot Wilcoxon v primeru uravnoteženih ali seznanjenih vzorcev.

-Statistika terapije z AI (AI-terapija.com), ki ima več običajnih testov opisnih statistik.

-Statistično za uporabo (fizika.CSBSJU.Edu/statistika), eden najstarejših, zato lahko vaš vmesnik izgleda zastarel, čeprav je zelo učinkovit brezplačni program.

Reference

1. Dietrichson. Kvantitativne metode: test razponov. Okrevano od: Bookdown.org
2. Marín J P. Vodnik SPSS: Analiza in postopki v neparametričnih testih. Okreval od: halweb.UC3M.je
3. USAL MOOC. Neparametrični test: U of Mann - Whitney. Obnovil od: YouTube.com
4. Wikipedija. U -test od Manna - Whitney. Okrevano od: je.Wikipedija.com
5. Xlstat. Center pomoči. Mann Test Tutorial - Whitney in Excel. Okrevano od: Pomoč.Xlsat.com