Porazdelitev hi-kvadrat (χ²), kako se izračuna, primeri

Dokaz Chi kvadrat tudi Ji-kvadrat (χ², Kjer je χ grško pismo, imenovano "chi"), se uporablja za določitev vedenja določene spremenljivke in tudi, ko želite vedeti, ali sta dve ali več spremenljivk statistično neodvisni.

Če želite preveriti vedenje spremenljivke, je treba poklicati test Chi kvadratni test prilagoditve. Vedeti, ali sta dve ali več spremenljivk statistično neodvisni od testa Chi kvadrat neodvisnosti, tudi poklican nepredvidljivih dogodkov.

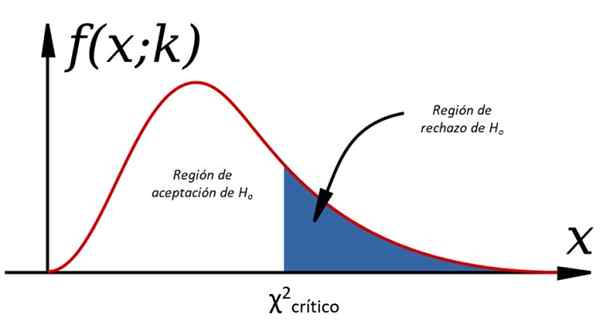
Slika 1. Hipotezni testi prek Chi Cuadrado

Ti dokazi so del statistične teorije odločitev, v kateri se preučuje populacija in sprejemajo odločitve o tem, analizirajo enega ali več vzorcev, ki so iz njega pridobljene. Za to je treba določiti določene predpostavke glede spremenljivk, imenovane hipoteza, ki so lahko ali ne.

Obstaja nekaj testov za kontrast teh domnev in določitev, ki so veljavni, znotraj določene mere zaupanja, vključno s testom Chi-kvadrat, ki ga je mogoče uporabiti za primerjavo dveh in večino populacij.

Kot bomo videli, se običajno upoštevata dve vrsti hipoteze o nekaterih populacijskih parametrah v dveh vzorcih: ničelna hipoteza, imenovana H_tudi (Vzorci so neodvisni) in alternativna hipoteza, označena kot H₁, (Vzorci so povezani), kar je v nasprotju s tem.

[TOC]

Kdaj se uporablja test s kvadratnim testom?

Chi kvadratni test velja za spremenljivke, ki opisujejo lastnosti, kot so spol, civilni status, krvna skupina, barva oči in nastavitve različnih vrst.

Test je zasnovan po želji:

-Preverite, ali je distribucija primerna za opis spremenljivke, ki se imenuje Prilagoditvena dobrota. Skozi test CHI Square lahko veste, ali obstajajo pomembne razlike med izbrano teoretično porazdelitvijo in opaženo frekvenčno porazdelitev.

-Vedite, ali sta dve spremenljivki X in Y neodvisni od statističnega vidika. To je znano kot Test neodvisnosti.

Ker velja za kvalitativne ali kategorične spremenljivke, se test s kvadratom CHI pogosto uporablja v družbenih vedah, administraciji in medicini.

Pogoji za uporabo

Za pravilno uporabo obstajata dve pomembni zahtevi:

Lahko vam služi: kakšen je odnos med območjem Rhombusa in pravokotnikom?

-Podatki morajo biti razvrščeni v frekvence.

-Vzorec mora biti dovolj velik, da bo porazdelitev kvadrata CHI veljavna, sicer je njegova vrednost precenjena in povzroči zavrnitev ničelne hipoteze, kadar ne bi smelo biti tako.

Splošno pravilo je, da če se v združenih podatkih pojavi frekvenca z vrednostjo manj kot 5, se ne uporablja. Če je več kot ena frekvenca manjša od 5.

Chi kvadratna porazdelitev

χ² Gre za nenehno porazdelitev verjetnosti. Obstajajo dejansko različne krivulje, odvisno od parametra k poklical Stopnje svobode naključno.

Njene lastnosti so:

-Območje pod krivuljo je enako 1.

-Vrednosti χ² So pozitivni.

-Porazdelitev je asimetrična, to je pristranskost.

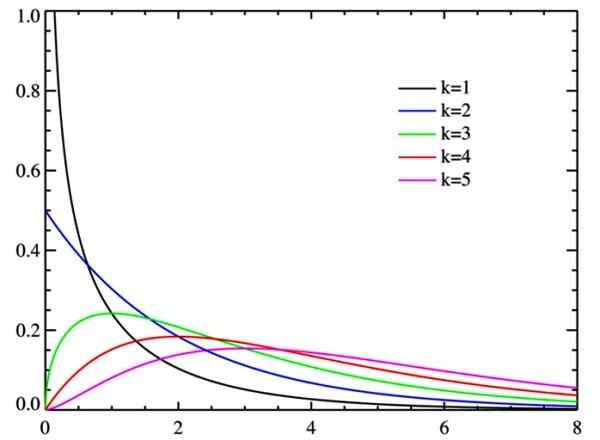Slika 2. Chi kvadratna porazdelitev za WATTS stopnje svobode. Vir: Wikimedia Commons.

Stopnje svobode

Ko se stopnje svobode povečujejo, se porazdelitev hi-kvadrat nagiba k normalni, kot je razvidno iz slike.

Za določeno porazdelitev se stopnje svobode določijo prek Tabela ob nepredvidljivih dogodkih, ki je tabela, v kateri so zabeležene opažene frekvence spremenljivk.

Če ima tabela F Ranke in c stolpci, vrednost k je:

K = (f - 1) ⋅ (c - 1)

Formulacija hipoteze

Ko je test CHI kvadrata nastavitev, se oblikujejo naslednje hipoteze:

-H_tudi: spremenljivka x ima porazdelitev verjetnosti f (x) s specifičnimi parametri in₁, in₂… In_str

-H₁: X ima še eno porazdelitev verjetnosti.

Porazdelitev verjetnosti, ki se domneva v ničelni hipotezi, je lahko na primer dobro znana normalna porazdelitev, parametri pa bi bili povprečni μ in standardni odklon σ.

Poleg tega je ničelna hipoteza ocenjena z določeno stopnjo pomena, to je merilo napake, ki bi bila narejena, ko jo zavračamo.

Na splošno je ta raven vzpostavljena 1 %, 5 % ali 10 % in nižji je rezultat testa, bolj zanesljiv je.

Vam lahko služi: mamica

In če se uporablja Chi kvadratni test nepredvidljivih dogodkov, kar, kot smo rekli, služi za preverjanje neodvisnosti med dvema spremenljivkama x in y, so hipoteze:

-H_tudi: Spremenljivka x in y sta neodvisna.

-H₁: X in y sta odvisna.

Ponovno je treba določiti stopnjo pomembnosti, da se pri odločitvi poznajo merilo napake.

Kako se izračuna statistika hi-kvadrat?

Statistični podatki Chi Square se izračunajo na naslednji način:

Simbol ∑ pomeni "seštevanje", ki ga moramo narediti o navedenem frakcijskem izrazu.

Vsota se izvaja od prvega razreda I = 1 do zadnjega, to je i = k.

Poleg:

-F_tudi To je opažena frekvenca (izvira iz dobljenih podatkov).

-F_in To je pričakovana ali teoretična frekvenca (treba jo je izračunati iz podatkov).

Če želite sprejeti ali zavrniti ničelno hipotezo, se izračuna χ² Za opazovane podatke in primerjamo z imenom, imenovano Chi kritični kvadrat, ki je odvisno od stopenj svobode k in raven pomembnosti α:

χ²_kritično =  χ²_{K, α}

Če na primer test želimo izvesti s stopnjo pomembnosti 1 %, potem α = 0.01, če bo s 5%, potem α = 0.05 in tako naprej. P, porazdelitveni parameter, kot je:

P = 1 - α

Te kritične kvadratne vrednosti so določene s tabelami, ki vsebujejo vrednost nakopičenega območja. Na primer za k = 1, ki predstavlja 1 stopnjo svobode in α = 0.05, enakovredno P = 1-.05 = 0.95, vrednost χ² Je 3.841.

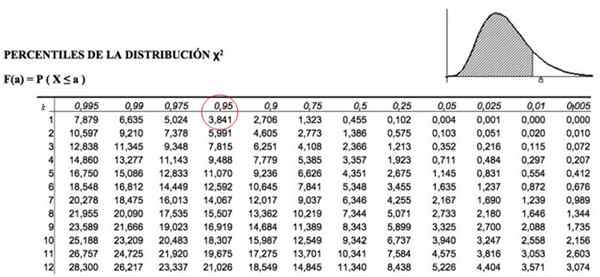Slika 3. Tabela vrednosti kvadratnih distribucijskih vrednosti. Vir: f. Zapata.

Merila za sprejem AC_tudi

Merila za sprejemanje h_tudi je:

-Da χ² < χ²_kritično  H_tudi, v nasprotnem primeru je zavrnjena (glej sliko 1).

Primer izračuna

V naslednji aplikaciji bo test kvadrata CHI uporabljen kot test neodvisnosti.

Predpostavimo, da raziskovalci želijo vedeti, ali je naklonjenost črni kavi povezana z žanrom osebe, in odgovor določiti s stopnjo pomena α = 0.05.

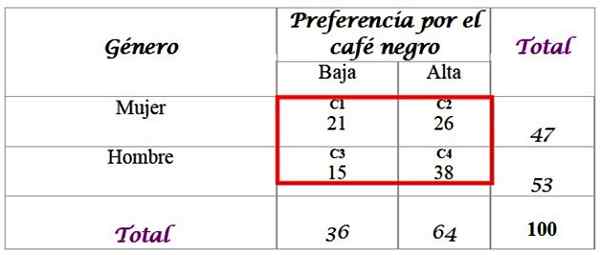
Vam lahko služi: zunanji nadomestni koti: vaje in vaje rešene

Za to je na voljo vzorec 100 anketiranih ljudi in njihovih odgovorov:

Korak 1

Vzpostavite hipoteze:

-H_tudi: spol in prednost črne kave sta neodvisna.
-H₁: Okus po črni kavi je povezan z žanrom osebe.

2. korak

Izračunajte pričakovane frekvence za porazdelitev, za katere so potrebne skupne dodane v zadnji vrstici in v desnem stolpcu. Vsaka celica v rdeči škatli ima pričakovano vrednost F_in, ki se izračuna tako, da se pomnoži skupno vrstico r vrstice F s celotnim stolpcem C, deljeno s skupnim vzorcem n:

F_in = (F x c) /n

Rezultati so naslednji za vsako celico:

-C1: (36 x 47) / 100 = 16.92
-C2: (64 x 47) / 100 = 30.08
-C3: (36 x 53) / 100 = 19.08
-C4: (64 x 53) / 100 = 33.92

Korak 3

Potem morate izračunati statistiko CHI Cuadrado za to porazdelitev v skladu z dano formulo:

χ²= [(21 - 16.92)² ÷ 16. 92] + [(26 - 30.08)² ÷ 30.08] + [(15 - 19.08)² ÷ 19.08]+ [(38 - 33.92)² ÷ 33. 92] = 0.9838 + 0.5534 + 0.8725 + 0.4908 = 2.9005

4. korak

Določite χ²_kritično, Če veste, da so registrirani podatki v F = 2 vrstici in C = 2 stolpci, je torej število stopenj svobode:

K = (2-1) ⋅ (2-1) = 1.

Kar pomeni, da moramo pogledati v tabelo, prikazano nad vrednostjo χ²_{K, α} = χ²_{1; 0.05} , kateri je:

χ²_kritično = 3.841

5. korak

Primerjajte vrednosti in se odločite:

χ² = 2.9005

χ²_kritično = 3.841

Od χ² < χ²_kritično Ničelna hipoteza je sprejeta in sklenjeno je, da naklonjenost črni kavi ni povezana z žanrom osebe, s stopnjo pomembnosti 5%.

Reference

1. Chi kvadratni test za neodvisnost. Okreval od: saylordotorg.GitHub.Io.
2. Med val. Statistični podatki, uporabljeni za zdravstvene vede: Ji-kvadrat test. Okreval od: Medwave.Cl.
3. Verjetnosti in statistike. Shi kvadratni test prilagoditve. Pridobljeno iz: Verjetnosti Andestics.com.
4. Triola, m. 2012. Osnovna statistika. 11. Izdaja. Addison Wesley.
5. Ne. Chi kvadratni test. Okrevano od: svetovalnega.Cuautitlan2.Ne.mx.