Formula in enačbe, primeri, vaja

The Kvazivna ocena, Kvasi varianta ali nezdrava odstopanje je statistično merilo razpršenosti podatkov a vzorec Glede povprečja. Vzorec je sestavljen iz niza podatkov, ki jih vzamejo iz večjega vesolja, imenovanega prebivalstvo.

Označeno je na več načinov, tukaj je bil izbran s_c² In za izračun sledi naslednja formula:

Slika 1. Opredelitev kvazivnosti. Vir: f. Zapata.

Kje:

-s_c ² = Quasiriance ali variance vzorca (varianta vzorca)

-x_Yo = Vsak od vzorčnih podatkov

-n = Število opazovanj

-X = Povprečje vzorca

Ker je enotnost vzorčne kvazivnosti kvadrat enote, v kateri pride vzorec, je v času razlage rezultatov raje sodelovati z kvazi standardni odklon ali standardni odklon vzorca.

To je označeno kot s_c In ga dobimo z ekstrahiranjem kvadratnega korena kvazivariance:

s_c = √ s_c ²

Kvazirianca je podobna varianci s², z edino razliko, ki je v imenovalcu N-1, Medtem ko je v različici, ga razdeli le n. Očitno je, da so, kadar je n zelo velik, vrednosti obeh ponavadi enake.

Ko je znana vrednost kvaziriance, lahko takoj veste, da je varianta.

[TOC]

Primeri kvazivnosti

Želite vedeti značilnosti katere koli populacije: ljudi, živali, rastlin in na splošno kakršne koli vrste predmetov. Toda analiza celotne populacije morda ni lahka naloga, še posebej, če je število elementov zelo veliko.

Nato se odvzamejo vzorci z upanjem, da njihovo vedenje odraža vedenje prebivalstva in tako lahko sklepa o tem, zahvaljujoč optimiziranim virom. To je znano kot statistični sklep.

Tu je nekaj primerov, v katerih kvazirianca in kvazi povezan standardni odklon služita kot statistični kazalnik, tako da poudarimo, da so rezultati, dobljeni v zvezi s povprečjem.

Lahko vam služi: obod kroga: kako ga odpeljati ven in formule, rešene vaje

1.- Direktor marketinga podjetja, ki izdeluje avtomobilske baterije, mora v mesecih oceniti povprečno trajanje baterije.

Če želite to narediti, naključno izberite vzorec 100 baterij, ki jih je kupila blagovna znamka. Podjetje ohrani evidenco podatkov o kupcih in jih lahko intervjuva, da pozna trajanje baterij.

Slika 2. Cuasive ocenjevanje je koristno za sklepanje in nadzor kakovosti. Vir: Pixabay.

2.- Akademsko upravljanje univerzitetne institucije mora oceniti registracijo naslednjega leta in analizirati število študentov, ki naj bi odobrili predmete, ki so trenutno v.

Na primer vsakega od odsekov, ki trenutno preučujejo fizični predmet I, lahko naslov izbere vzorec študentov in analizira njegovo uspešnost v omenjenem stolu. Na ta način lahko sklepate, koliko študentov bo v naslednjem obdobju študiralo fiziko II.

3.- Skupina astronomov osredotoča svojo pozornost na del neba, kjer opazimo določeno število zvezd z določenimi značilnostmi: velikost, masa in temperatura na primer.

Vredno se je vprašati, ali bodo zvezde v drugi podobni regiji imele iste značilnosti, vključno z zvezdami v drugih galaksijah, kot so sosednji oblaki Magallane ali Andromeda.

Zakaj se razdelite med N-1?

V kvaziriranju je razdeljen med N-1 namesto n In zato, ker je kvazirianca a Vztrajal ocenjevalec, Kot je navedeno na začetku.

Zgodi se, da je iz iste populacije mogoče izvleči veliko vzorcev. Tudi odstopanje vsakega od teh vzorcev je mogoče povprečiti, vendar se povprečje teh odstopanj ne izkaže za enako odstopanjem populacije.

Vam lahko služi: relativna vrednost

Pravzaprav povprečje odstopanj vzorca podcenjuje odstopanje populacije, razen če se ne uporablja N-1 V imenovalniku. Preveriti je mogoče, da pričakovana vrednost kvaziznosti e (-e_c²) je natančno s².

Zato je rečeno, da je kvazirianca neobdelana in je boljši ocenjevalec variance populacije s².

Alternativni način izračuna navidezne ocene

Zlahka je dokazati, da lahko kvazirianca izračunamo tudi na naslednji način:

s_c² = [∑x² / (N -1)] - [∑nx² / (N-1)]

Standardni rezultat

Z odstopanjem od vzorca lahko vemo, koliko standardnih odstopanj ima določeno vrednost x, bodisi nad ali pod povprečjem.

Za to se uporablja naslednji dimenzijski izraz:

Standardni rezultat = (x - x) / s_c

Vaja rešena

Izračunajte Quasiriance in kvazi tipično odstopanje naslednjih podatkov, ki so sestavljene iz mesečnih plačil v $, ki jo je zavarovalnica opravila na zasebni kliniki.

863 903 957 1041 1138 1204 1354 1624 1698 1745 1802 1883

a) Uporabite definicijo kvazivnosti, podane na začetku, in rezultat preverite tudi z alternativnim obrazcem, navedenim v prejšnjem razdelku.

b) Izračunajte standardno oceno drugih podatkov, branje od zgoraj navzdol.

Rešitev

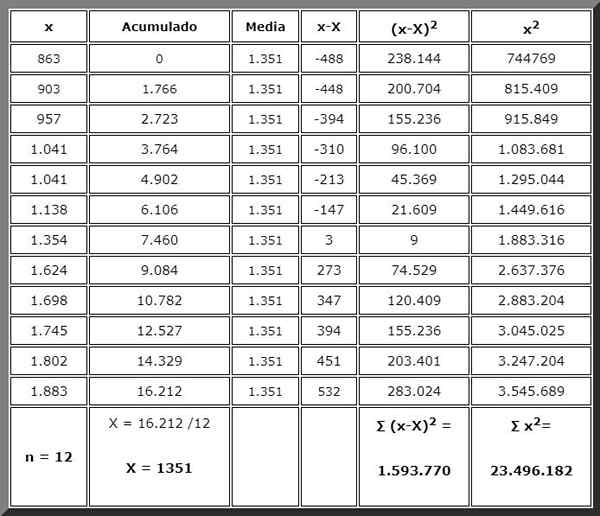
Težavo lahko rešimo ročno s pomočjo preprostega ali znanstvenega kalkulatorja, za katerega moramo nadaljevati po vrstnem redu. In za to ni nič boljšega kot organiziranje podatkov v tabeli, kot je prikazana spodaj:

Zahvaljujoč tabeli, ki ste jo organizirali informacije, in zneske, ki bodo potrebne v formulah, so na koncu ustreznih stolpcev, pripravljeni za takojšnjo uporabo. Povzeti so prikazani krepko.

Vam lahko služi: kakšnih je 7 elementov oboda?

Povprečni stolpec se vedno ponovi, vendar se splača, ker je primerno imeti vrednost na ogled, da zapolnite vsako vrstico tabele.

Končno se uporablja enačba za kvaziričnost na začetku, samo vrednosti se zamenjajo in glede na vsoto že imamo izračunano:

s_c² = 1.593.770 / (12-1) = 1.593.770 /11 = 144.888.2

To je vrednost kvaziriranosti in njene enote so "dolarji na kvadrat", kar nima veliko praktičnega smisla, zato se izračunajo standardni kvazi vzorca, kar ni nič drugega kot kvadratni koren kvazivarijance:

s_c = (√144.888.2) $ = 380,64 $

Takoj je podkrepljeno, da je ta vrednost pridobljena tudi z alternativno obliko kvazivarijanca. Potrebna vsota je na koncu zadnjega stolpca na levi:

s_c² = [∑x² / (N-) - [∑nx² / (N-1)] = [23.496.182/11] - [12 x 1351²/ enajst]

= 2.136.016.55 - 1.991.128,36 = 144.888 dolarjev na kvadrat

Je enaka vrednost, pridobljena s formulo, ki je bila dana na začetku.

Rešitev b

Druga vrednost od zgoraj navzdol je 903, njegova standardna ocena je

Standardni rezultat 903 = (x - x) / s_c = (903 - 1351)/380.64 = -1.177

Reference

1. Canavos, g. 1988. Verjetnost in statistika: aplikacije in metode. McGraw Hill.
2. Devore, j. 2012. Verjetnost in statistika za inženirstvo in znanost. 8. Izdaja. Cengage.
3. Levin, r. 1988. Statistika za skrbnike. 2. mesto. Izdaja. Dvorana Prentice.
4. Ukrepi disperzije. Okreval od: Thales.CICA.je.
5. Walpole, r. 2007. Verjetnost in statistika za inženirstvo in znanost. Pearson.