Kakšen je statistični razpon? (S primeri)

On domet, Ogled ali amplituda v statistiki je razlika (odštevanje) med največjo vrednostjo in najnižjo vrednostjo nabora podatkov iz vzorca ali populacije. Če je razpon s črko r in podatki predstavljen s pomočjo x, Formula za območje je preprosto:

R = x_Max - x_min

 Kjer x_Max Je največja vrednost podatkov in x_min Je minimalno.

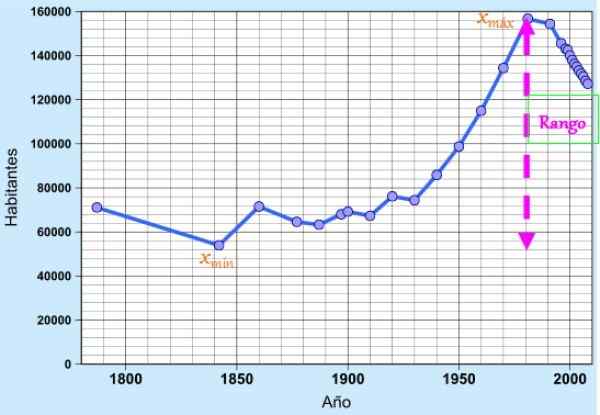
Slika 1. Obseg podatkov, ki ustrezajo prebivalstvu Cádiza v zadnjih dveh stoletjih. Vir: Wikimedia Commons.

Koncept je zelo uporaben kot preprost disperzijski ukrep, da hitro cenite spremenljivost podatkov, saj kaže na razširitev ali dolžino intervala, kjer jih najdemo.

Recimo na primer stas skupine 25 moških študentov prvega leta inženiringa na univerzi. Najvišji študent v skupini Ukrepi 1.93 m in najnižja 1.67 m. To so skrajne vrednosti vzorčnih podatkov, zato je pot le -teh:

R = 1.93 - 1.67 M = 0.26 m ali 26 cm.

Stas študentov te skupine je distribuiran po vsem tem območju.

[TOC]

Prednosti in slabosti

Obseg je, kot smo že rekli, merilo, kako razpršeni so podatki. Majhen razpon kaže, da so podatki bolj ali manj blizu in disperzija je malo. Po drugi strani je večji razpon kaže, da so podatki bolj razpršeni.

Prednosti izračuna območja so očitne: zelo preprosto in hitro je najti, ker je preprosta razlika.

Ima tudi enake enote kot podatki, s katerimi deluje, in koncept je zelo enostavno razlagati za vsakega opazovalca.

V primeru stasa študentov inženiringa, če bi bil doseg 5 cm, bi rekli, da so študenti enake velikosti. Toda z razponom 26 cm takoj domnevamo, da so v vzorcu študenti vseh vmesnih stanj. Ali ta predpostavka vedno v redu?

Lahko vam služi: razlika med krogom in obodom (s primeri)

Slabosti območja kot disperzijski ukrep

Če natančno pogledamo, v našem vzorcu 25 študentov inženirstva le eden od njih meri 1.93 in preostalih 24 ima stature blizu 1.67 m.

In vendar obseg ostaja enak, čeprav je povsem mogoče, da se pojavi nasprotno: da stas večine niha okoli 1.90 m in samo en ukrep 1.67 m.

Vsekakor je porazdelitev podatkov zelo različna.

Slabosti območja kot disperzijskega ukrepa so posledica dejstva, da uporablja le skrajne vrednosti in ignorira vse ostale. Ker je večina informacij izgubljena, ni pojma, kako se vzorčni podatki porazdelijo.

Druga pomembna značilnost je, da se obseg vzorca nikoli ne zmanjšuje. Če dodamo več informacij, to je, upoštevamo več podatkov, se obseg poveča ali ostane enak.

In vsekakor je uporabna le pri delu z majhnimi vzorci, njegova edinstvena uporaba ni priporočljiva kot merilo disperzije v velikih vzorcih.

Kar je treba storiti, je dopolniti z izračunom drugih disperzijskih ukrepov, ki upoštevajo podatke, ki jih zagotavljajo skupni podatki: Pot Interquartilic, odstopanje, standardni odklon in koeficient variacije.

Interquirile poti, kvartili in rešeni primer

Spoznali smo, da je šibkost območja kot disperzijskega ukrepa ta, da uporablja le skrajne vrednosti porazdelitve podatkov, drugim pa izpusti.

Da se izognemo tej nevšečnosti kvartile: tri vrednosti, znane kot Pozicijski ukrepi.

Podatke, ki niso razvrščene v štiri dele (drugi široko uporabljeni položaj, so Decili in odstotek). To so njegove značilnosti:

-Prvi četrti Q₁ Vrednost podatkov je tako, da je 25 % vseh manj kot Q₁.

Vam lahko služi: konstantna sorazmernost: kaj je, izračun, vaje

-Drugi kvartil q₂ Je mediana porazdelitve, kar pomeni, da je polovica (50 %) podatkov manjša od te vrednosti.

-Končno tretji kvartil Q₃ poudarja, da je 75 % podatkov manj kot Q₃.

Nato je interkvotilni razpon ali interkvartilna pot opredeljena kot razlika med tretjim kvartilom Q₃ in prvi kvartil q₁ podatkov:

Interquotile Journey = R_Q = Q₃ - Q₁

Na ta način vrednost ranga r_Q Na to ne vplivajo skrajne vrednosti. Zato je priporočljivo uporabiti, ko gre za pristranske porazdelitve, na primer zelo visoke ali zelo nizke študente, opisane zgoraj.

- Izračun cuartyles

Obstaja več načinov za njihovo izračun, tukaj bomo predlagali enega, vsekakor pa je treba vedeti število naročil »N_tudi", Kar je kraj, ki zavzema ustrezen kvartil v distribuciji.

To je, če na primer izraz, ki ustreza Q₁ je druga, tretja ali četrta in tako na distribuciji.

Prvi kvartil

N_tudi (Q₁) = (N+1) / 4

Drugi kvartil ali mediana

N_tudi (Q₂) = (N+1) / 2

Tretji kvartil

N_tudi (Q₃) = 3 (n+1) / 4

Kjer je n številka podatkov.

Mediana je vrednost, ki je prava sredi distribucije. Če je številka podatkov čudna, ni težav pri iskanju, če pa je celo, potem sta dve osrednji vrednosti v povprečju, da ju spremenita v eno.

Ko je izračunana številka naročila, se upošteva eno od teh treh pravil:

-Če nimate decimalk, se zahtevajo podatki, navedeni v distribuciji, in to bodo četrti iskani.

-Ko je številka naročila na pol poti med dvema, potem so podatki, ki jih prikazuje celoten del z naslednjim dejstvom, povprečno in rezultat je ustrezen četrti.

-V katerem koli drugem primeru je najbližje celo število zaokroženo in to bo četrto mesto.

Vam lahko služi: načelo aditiva

Rešen primer

Na lestvici od 0 do 20 je skupina 16 študentov matematike v delnem izpitu pridobila naslednje ocene (točke):

16, 10, 12, 8, 9, 15, 18, 20, 9, 11, 1, 13, 17, 9, 9, 10, 14

Najti:

a) Podatki ali podatkovna pot.

b) Vrednosti kvartilov q₁ in q₃

c) Interquartil razpon.

Slika 2. Ali kvalifikacije tega izpita za matematiko naredijo toliko spremenljivosti? Vir: Pixabay.

Rešitev

Prva stvar, ki jo je treba najti, je naročiti, da se podatki povečujejo ali zmanjšujejo. Na primer v povečanju vrstnega reda imate:

1, 8, 9, 9, 9, 10, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20

Skozi formulo, podano na začetku: r = x_Max - x_min

R = 20 - 1 točke = 19 točk.

Glede na rezultat imajo te ocene odlično razpršitev.

Rešitev b

N = 16

N_tudi (Q₁) = (N + 1) / 4 = (16 + 1) / 4 = 17/4 = 4.25

To je številka z decimali, katerih celoten del je 4. Nato gremo na distribucijo, podatki, ki zasedajo četrto mesto. Ker sta oba 9, je povprečje tudi 9 in nato:

Q₁ = 9

Zdaj ponovimo postopek za iskanje Q₃:

N_tudi (Q₃) = 3 (n +1) / 4 = 3 (16 +1) / 4 = 12.75

Spet je decimalna, a ker ni na polovici poti, je zaokrožena na 13. Iskani kvartil zaseda trinajsti položaj in je:

Q₃ = 16

Rešitev c

R_Q = Q₃ - Q₁ = 16 - 9 = 7 točk.

To, kot vidimo, je veliko manj od podatkovnega območja, izračunanega v oddelku A), ker je bila najnižja ocena 1 točka, vrednost, ki je veliko dlje od ostalih.

Reference

1. Berenson, m. 1985. Statistični podatki za upravo in ekonomijo. Interameriški s.Do.
2. Canavos, g. 1988. Verjetnost in statistika: aplikacije in metode. McGraw Hill.
3. Devore, j. 2012. Verjetnost in statistika za inženirstvo in znanost. 8. Izdaja. Cengage.
4. Primeri kvartilov. Pridobljeno iz: matematika10.mreža.
5. Levin, r. 1988. Statistika za skrbnike. 2. mesto. Izdaja. Dvorana Prentice.
6. Walpole, r. 2007. Verjetnost in statistika za inženirstvo in znanost. Pearson.