Ukrepi osrednje težnje po združenih formulah podatkov, vaje

The trendni ukrepi osrednje Navajajo vrednost, okoli katere so podatki o distribuciji. Najbolj znano je povprečje ali aritmetično povprečje, ki je sestavljeno pri dodajanju vseh vrednosti in deljenju rezultata s skupnim številom podatkov.

Če pa je porazdelitev sestavljena iz velikega števila vrednosti in ni urejena, ni enostavno izvesti potrebnih izračunov za pridobivanje dragocenih informacij, ki jih vsebujejo.

Slika 1. Ukrepi osrednje tendence za združene podatke so dobro kažejo na splošno vedenje podatkov

Zato so razvrščeni v razrede ali kategorije, da bi izpostavili a porazdelitev Frekvence. Izvedba tega prejšnjega vrstnega reda podatkov je lažje izračunati ukrepe osrednje težnje, med katerimi so:

-Polovica

-Mediana

-Moda

-Geometrijska srednja

-Harmonična srednja

Formule

Spodaj imamo formule osrednjih ukrepov tendenc za združene podatke:

Aritmetično povprečje

Povprečje se najbolj uporablja za karakterizacijo kvantitativnih podatkov (številčne vrednosti), čeprav je precej občutljiv na skrajne vrednosti porazdelitve. Izračuna se:

Z:

-X: povprečna ali povprečna aritmetika

-F_Yo: frekvenca razreda

-m_Yo: Blagovna znamka

-G: Številka razredov

-N: Skupni podatki

Mediana

Če želite izračunati, je treba najti interval, ki vsebuje opazovanje N/2 in interpolar, da določimo numerično vrednost omenjenega opazovanja s pomočjo naslednje formule:

Kje:

-C: intervalna širina, ki ji pripada mediana

-B_M: spodnja meja omenjenega intervala

-F_m: Število opazovanj v intervalu

-N/2: Skupni podatki, deljeni z 2.

-F_Bm: Število opazovanj pred intervalom, ki vsebuje mediano.

Zato je mediana ukrep položaja, to je, da nabor podatkov deli na dva dela. Prav tako jih je mogoče določiti kvartile, Decili in odstotek, ki razdelijo porazdelitev na štiri, deset in sto delov.

Vam lahko služi: Fourierjeva transformacija: lastnosti, aplikacije, primeri

Moda

V združenih podatkih se išče razred ali kategorija, ki vsebuje večino opazovanj. To je Modalni razred. Porazdelitev ima lahko dve ali več mode, v tem primeru se imenuje bimodalni in Multimodalno, oziroma.

Modo lahko izračunate tudi v združenih podatkih po enačbi:

Z:

-L₁: Spodnja meja razreda, kjer je moda

-Δ₁: Ostane med frekvenco modalnega razreda in frekvenco razreda, ki je pred njim.

-Δ₂: odštejte med frekvenco modalnega razreda in frekvenco razreda, ki mu sledi.

-C: interval širine, ki vsebuje modo

Harmonična srednja

Harmonično srednjo vrednost označuje h. Ko imate nabor n vrednosti x₁, x₂, x₃…, Harmonična srednja vrednost je obratna ali vzajemna aritmetična srednja vrednost inverzne vrednosti.

Lažje ga je videti skozi formulo:

In ko ima združene podatke, se izraz spremeni v:

Kje:

-H: harmonično povprečje

-F_Yo: frekvenca razreda

-m_Yo: Razredna znamka

-G: Številka razredov

-N = f₁ + F₂ + F₃ +..

Geometrijska srednja

Če imate n pozitivne številke x₁, x₂, x₃…, Njegova geometrijska srednja vrednost se izračuna z N-EM-om izdelka vseh števil:

V primeru združenih podatkov je mogoče dokazati, da je decimalni logaritem geometrijskega povprečnega dnevnika G podan z:

Kje:

-G: geometrijska srednja vrednost

-F_Yo: frekvenca razreda

-m_Yo: Blagovna znamka

-G: Številka razredov

-N = f₁ + F₂ + F₃ +..

Razmerje med H, G in X

Vedno je res, da:

H ≤ g ≤ x

Najbolj uporabljene definicije

Naslednje definicije so potrebne za iskanje vrednosti, opisanih v prejšnjih formulah:

Frekvenca

Frekvenca je opredeljena kot številokrat ponovitev dejstva.

Domet

Je razlika med glavno in manjšo vrednostjo, ki je prisotna v distribuciji.

Število razredov

Če želite vedeti, koliko razredov razvrstimo v podatke, uporabljamo nekaj meril, na primer naslednje:

Vam lahko služi: 17 utemeljenih težav

Meje

Kličejo se ekstremne vrednosti vsakega razreda ali intervala meje in vsak razred ima lahko dobro določene meje, v tem primeru pa ima spodnjo mejo in eno večjo. Ali ima lahko odprte meje, ko je podan razpon, na primer vrednosti, večje ali nižje od določenega števila.

Blagovna znamka razreda

Preprosto je sestavljen iz sredine intervala in se izračuna v povprečju zgornje meje in spodnje meje.

Interval širina

Podatke je mogoče razvrstiti v razrede enake ali različne velikosti, to je širina ali amplituda. Prva možnost je najbolj uporabljena, saj olajša izračune, čeprav je v nekaterih primerih nujno, da imajo razredi različne širine.

Širina c Iz intervala ga lahko določimo z naslednjo formulo:

C = domet / n_c

Kje_c To je število razredov.

Vaja rešena

Spodaj imamo vrsto meritev hitrosti v km/h, opravljene z radarjem, ki ustrezajo 50 avtomobilih, ki so v določenem mestu šli skozi ulico:

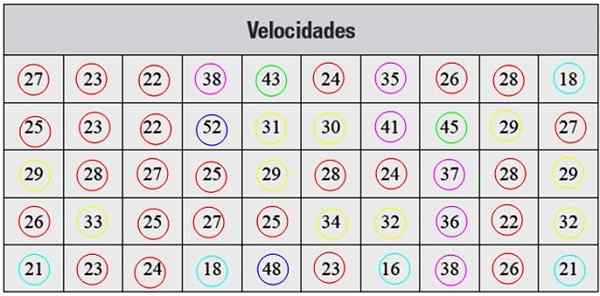Slika 2. Tabela za reševanje vaje. Vir: f. Zapata.

Rešitev

Predstavljeni podatki niso organizirani, zato je prvi korak, da jih razvrstite v razrede.

Koraki za razvrščanje podatkov in izdelavo tabele

Korak 1

Poiščite območje R:

R = (52 - 16) km/h = 36 km/h

2. korak

Izberite število razredov n_c, V skladu z danimi merilomi. Ker je 50 podatkov, lahko izberemo n_c = 6.

Korak 3

Izračunajte širino c intervala:

C = domet /n_c = 36/6 = 6

4. korak

Obrazecni razredi in podatki o skupini na naslednji način: Za prvo mejo razreda A je izbran takoj, ko je v to vrednost C = 6, ki je predhodno izračunana, dodana spodnja vrednost, ki je prisotna v tabeli, in tako dobi zgornjo mejo prvi razred.

Nastane na enak način za izgradnjo preostalih razredov, kot je prikazano v naslednji tabeli:

Vam lahko služi: kaj je številka capicúa? Lastnosti in primeri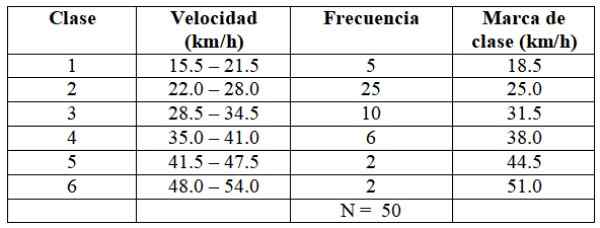

Vsaka frekvenca ustreza barvi na sliki 2.

Povprečni izračun

X = (5 x 18.5 +25 x 25.0 + 10 x 31.5 + 6 x 38.0 + 2 x 44.5 + 2 x 51.0) ÷ 50 = 29.03 km/h

Srednji izračun

Mediana je v razredu 2 tabele, saj obstaja prvih 30 podatkov o distribuciji.

-Intervalna širina, ki ji pripada mediana: c = 6

-Spodnja meja intervala, kjer je mediana: b_M = 22.0 km/h

-Število opazovanj v intervalu F_m = 25

-Skupni podatki, deljeni z 2: 50/2 = 25

-Število opazovanj pred intervalom, ki vsebuje mediano: f_Bm = 5

In operacija je:

Mediana = 22.0 + [(25-5) ÷ 25] × 6 = 26.80 km/h

Moda

Moda najdemo tudi v razredu 2:

-Interval Širina: C = 6

-Spodnja meja razreda, kjer najdemo modo: l₁ = 22.0

-Odštejte med frekvenco modalnega razreda in frekvenco razreda, ki je pred njim: δ₁ = 25-5 = 20

-Odštejte med frekvenco modalnega razreda in frekvenco razreda, ki sledi: δ₂ = 25 - 10 = 15

S temi podatki je operacija:

Moda = 22.0 + [20 ÷ (20 + 15)] x6 = 25.4 km/h

Izračun geometrijske srednje

N = f₁ + F₂ + F₃ +... = 50

dnevnik g = (5 x dnevnik 18.5 + 25 x log 25 + 10 x log 31.5 + 6 x dnevnik 38 + 2 × log 44.5 + 2 x log 51) /50 =

dnevnik g = 1.44916053

G = 28.13 km/h

Harmonični srednji izračun

1/h = (1/50) x [(5/18.5) + (25/25) + (10/31.5) + (6/38) + (2/44.5) + (2/51)] = 0.0366

H = 27.32 km/h

Povzetek ukrepov centralnih tendenc

Enote spremenljivk so KM/H:

-Mediji: 29.03

-Mediana: 26.80

-Moda: 25.40

-Geometrijski mediji: 28.13

-Harmonična srednja: 27.32

Reference

1. Berenson, m. 1985. Statistični podatki za upravo in ekonomijo. Interameriški s.Do.
2. Canavos, g. 1988. Verjetnost in statistika: aplikacije in metode. McGraw Hill.
3. Devore, j. 2012. Verjetnost in statistika za inženirstvo in znanost. 8. Izdaja. Cengage.
4. Levin, r. 1988. Statistika za skrbnike. 2. mesto. Izdaja. Dvorana Prentice.
5. Spiegel, m. 2009. Statistika. Serija Schaum. 4 ta. Izdaja. McGraw Hill.
6. Zdravljenje združenih podatkov. Okreval od: Itchihuahua.Edu.mx.
7. Walpole, r. 2007. Verjetnost in statistika za inženirstvo in znanost. Pearson.