Ohranjanje načela linearne trenutke, primeri, vaje.

The ohranjanje linearnega zagona telesa ugotovi, da je produkt njegove mase s svojo hitrostno vektorjo konstantna količina, ko telo brez interakcije z drugimi telesi in s hitrostjo, izmerjeno glede na fiksni ali neakutni referenčni sistem.

Ko je več teles, ki med seboj delujejo samo, vendar ne z zunanjim okoljem, potem linearni zagon sčasoma ostane tudi konstanten.

Astronavt v vesolju je brez vseh interakcij, zato je njegov linearni trenutek

Linearni trenutek, količina linearnega gibanja ali preprosto zagon, Označeno je s pismom str In to je vektorski znesek:

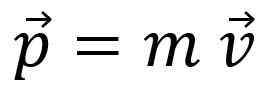
Linearni trenutek ni enak hitrosti, čeprav je razmerje očitno: na primer tovornjak, ki gre na 20 km/h, ima več linearnega časa kot kolo, ki se premika z isto hitrostjo.

Da se linearni trenutek telesa spremeni, je treba, da nanjo deluje neto zunanja sila, sicer ostaja konstantna. Poleg tega linearni trenutek Str sistema, ki ga oblikuje N-telo To je vektorska vsota posameznih trenutkov:

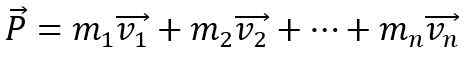
[TOC]

Načelo ohranjanja količine linearnega gibanja

V telesu, brez sil (ali tistega, v katerem so vse sile na njem preklicane), se zgodi, da se linearni trenutek.

Na enak od.

To načelo ohranjanja je navedeno tako:

Skupni linearni trenutek nabora N-telesa, ki medsebojno deluje samo, vendar ne z zunanjim okoljem.

In matematično je izraženo na naslednji način:

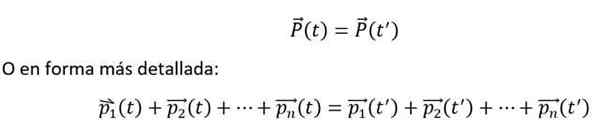
Prejšnja enakost je izpolnjena, če in samo, če n-telesa sodelujejo med seboj, vendar ne z zunanjim okoljem. Poleg tega je treba posamezne trenutke vedno izmeriti glede na inercialni referenčni sistem.

Primeri

Primer 1

Dva astronavta v vesolju se vzameta iz rok in ostaneta v fiksnem položaju glede na ladjo. Vendar se medsebojno potiskajo, začnejo se ločiti v nasprotnih smereh, ko jih vidimo z ladje.

Lahko vam služi: Teorija velikega poka: značilnosti, stopnje, dokazi, problemi

V tem primeru, ker je interakcija med astronavti le med njimi skozi kontaktno silo njihovih rok, skupni linearni trenutek. To pomeni, da je skupni linearni čas 0.

Vendar se je linearni trenutek vsakega astronavta spremenil. Sprva je imela vsak linearni trenutek 0 glede na ladjo, toda po potiskanju enega izide v eno smer in drugega v nasprotni smeri, z ne-null linearnimi trenutki enake velikosti in nasprotnimi naslovi.

Ko se posamezni trenutki dodajo vektorsko, se kot rezultat dobiva začetni skupni linearni zagon, ki je praznina.

Po drugi strani pa ohranjanje linearnega trenutka znesek. Toda rezultat pomnožitve njegove mase s hitrostjo je enak izdelku, pridobljenem z množenjem mase drugega s hitrostjo drugega.

Primer 2

Mladica je na plavajoči ploščadi v jezeru mirnih voda in njegov lastnik ga vidi s pristanišča. Na začetku sta tako platforma kot psička v mirovanju, toda ko se mladič želi približati lastniku, se platforma oddalji od pristanišča.

Pojasnilo tega opazovanja je natančno v načelu ohranjanja linearne zneske. Sistem je sestavljen iz mladička in platforme.

Mladica se lahko sprehodi po ploščadi zahvaljujoč sili trenja med nogami in površino, v tem primeru pa je trenje notranja sila interakcije med njim in platformo.

Set je izoliran sistem, ploščad pa se lahko premika vodoravno na jezeru, brez vsega odpornosti. Po drugi strani pa so v navpični smeri vse sile ravnovesje in kompenzirane, nabor pa v tej smeri nima gibanja.

Zato so v tej situaciji vse hipoteze izpolnjene tako, da se uporablja načelo ohranjanja linearnega zagona.

Primer 3

Eskimo je ujet v središču sladoleda, led je tako gladek, da ne glede na to, koliko preizkusi, Eskimo zdrsne in vedno ostane na istem mestu.

Edini možen način, ki ga Eskimo zapusti jezero, je, da leži v smeri, v nasprotju s katerim težkim predmetom, ki nosi v nahrbtniku (ob predpostavki.

Vam lahko služi: geometrijska optika: katere študije, zakoni, aplikacije, vaje

Prijave

Ladja v vesolju

Ohranitev linearnega trenutka. V tem primeru se impulz ladje doseže z izgonom plinov z veliko hitrostjo, tako da se lahko raketa premika v nasprotni smeri, v katero so jim izgnali.

Če je ladja prvotno v mirovanju, ko gorivo gori in izgnano, se sila izgona zgodi proti sami ladji. To je notranja sila med plini in ladjo. Zunanjih sil ni in zato uporablja ohranjanje linearnega trenutka.

Ker je linearni trenutek plinov enak in v nasprotju z ladjo, uspe zapustiti počitek in z nadaljevanjem izgona plinov povečuje svojo količino gibanja in s tem hitrost.

Vsakodnevno zivljenje

Še en primer za ohranjanje linearnega trenutka.

Lahko bi trdili, da v tem primeru načelo ne velja, ker obstaja zunanja sila: upor, ki ga ponuja les na klinček.

Vendar je v času stika sila, ki jo kladivo natisne na noht.

Celoten linearni trenutek kladiva, ki je zaradi velike mase in hitrosti precej velik, se prenese na žebelj tik po trčenju. Upoštevajte, da se ves trenutek prenese, vendar ne vsa kinetična energija kladiva, saj se del tega pretvori v toplotno energijo v noht in kladivo, ki po udarcu dvignejo temperaturo.

Vaje

Vaja 1

Astronavti Andrew in Berenice sta zunaj vesoljske postaje, vzeta iz obeh rok in v mirovanju glede na postajo. Vožnja si potiskajo roke proti drugim in so izpuščeni. Če Andrew, se 70 kg mase premakne na 1 m/s glede postaje, kar je hitrost Berenice s 49 kg mase?

Rešitev

V tem primeru se jasno uporablja hipoteza o ohranjanju linearnega zagona, saj v zunanjem prostoru ni zunanjih sil. Sila, s katero njihove roke potisnejo oba astronavta, je notranja sila.

Lahko vam služi: valovna difrakcija: koncept in primeri

Recimo, da je Andrejeva masa m_do in to berenice m_b. Podobno so hitrosti obeh po impulzu V_do Za Andrewa in V_b Za Berenice. Nato se ohrani linearni zagon uporablja na naslednji način:

M_do∙0 + M_b∙0 = M_do∙V_do+ M_b∙V_b

Odstranjevanje hitrosti Berenice imate:

V_b = - (m_do / M_b) ∙ V_do

Postavitev številčnih vrednosti:

V_b = - (70/49) ∙ (1m / s) ali = -1,43m/s ali

To pomeni, da se Berenice hitro premika 1,43 m/s v nasprotni smeri Andreja.

Vaja 2

Mladič se sprehodi proti svojemu lastniku na pol premeščene ploščadi. Vir: f. Zapata.

5 kg testo je v mirovanju na 15 kg ploščadi, ki plava, tudi v mirovanju, na mirujočem jezeru. Če mladiček začne hoditi po ploščadi s hitrostjo 0,5 m/s glede tega. Kako hitro bosta mladica in platforma glede fiksnega opazovalca?

Rešitev

Bomlje se kot inercialni referenčni sistem na dok, kjer je lastnik mladička. Sprva tako mladič kot plavajoča ploščad v mirovanju v mirovanju pri pristanišču.

Ko se mladiček odloči hitro stopiti proti lastniku V ' Kar zadeva platformo, se platforma s hitrostjo oddaljuje od pomladi +V. Hitrost mladička glede na dok doseže vektorsko vsoto njene hitrosti glede na platformo in hitrost platforme in jo označuje z:

v = -v' + V

Ker je odpornost vode na gibanje ploščadi praktično ničla zaradi nizke hitrosti, potem je mogoče potrditi, da sistem sestavljen iz Mladič + platforma Gre za osamljen sistem in uporabljeno je načelo ohranjanja linearnega zagona:

0 = m ∙ v + m ∙ V

Če se spomnite, da je v ' + V imate:

0 = -M ∙ V ' + M ∙ V + M ∙ V

To je: m ∙ v '= (m+m) ∙ V

Zato je v = [m/(m + m)] v 'y v = - (m/m) v = - [m/(m + m)] v'

Zamenjava numeričnih vrednosti je:

V = [5/(5 +15)] ∙ 0,5m/s = 0,125 m/s

To je hitrost, s katero se pomladna ploščad premakne.

V = -(15/20) ∙ 0,5m/s = -0,375 m/s

In to je hitrost, s katero se mladiček približa pristanišču.

Reference

1. Univerza Duke. Sistemi delcev. Okrevano od: webhome.Phy.vojvoda.Edu.
2. Rex, a. 2011. Osnove fizike. Pearson.
3. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1. Pearson.
4. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7. Ed. Cengage učenje.
5. Tipler, str. (2006). Fizika za znanost in tehnologijo. 5. izd. Zvezek 1. Uredništvo se je vrtelo.