Končne nastavljene lastnosti, primeri, rešene vaje

Razume ga Končni komplet vsi nastavljeni z omejenim ali računovodskim številom elementov. Primeri končnih kompletov so marmori, ki so v vrečki, naboru domov v soseski ali kompletu Str tvori dvajset (20) naravnih števil:

Str = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,13, 14, 16, 17, 18, 19, 20 20 

Nabor zvezd Universe je zagotovo neizmeren, vendar zagotovo ni znan, ali je končna ali neskončna. Vendar je nabor planetov sončnega sistema končen.

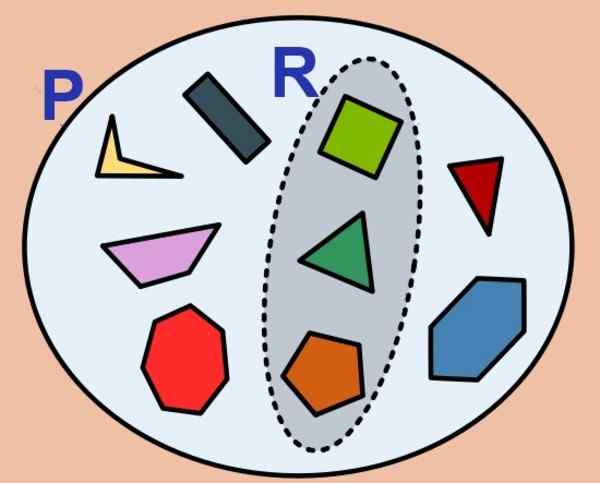
Slika 1. Nabor poligonov je končen in tudi podskupina običajnih. (Wikimedia Commons)

Število elementov končnega niza se imenuje njegova kardinalnost in za komplet Str Tako je označeno kot ta: kartica (Str) bodisi #Str. Prazen komplet ima ničelno kardinalnost in velja za končni komplet.

[TOC]

Lastnosti

Med lastnostmi končnih nizov so naslednje:

1- Zveza končnih nizov ima za posledico nov končni komplet.

2- Če sta prestrežena dva končna kompleta, je nov končni komplet.

3- Podskupina končnega niza je končna, njegova kardinalnost.

4- Prazen komplet je končni komplet.

Primeri

Obstaja veliko primerov končnih sklopov. Med nekaterimi primeri so naslednji:

Set M mesecev v letu, ki jih je mogoče razširiti na naslednji način:

M = Januar, februar, marec, april, maj, junij, julij, avgust, september, november, december, kardinalnost M je 12.

Set S dni v tednu: S = Ponedeljek, torek, sreda, četrtek, petek, sobota, nedelja. Kardinalnost s je 7.

Vam lahko služi: odnosi s sorazmernostjo: koncept, primeri in vaje

Set Ñ Iz črk španske abecede je končni niz, ta komplet po razširitvi je napisan tako:

Ñ = A, B, C, D, E, F, G, H, I, J, K, L, M, N, ñ, O, P, Q, R, S, T, U, V, V, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, X, Y, Z in ITS Kardinalnost je 27.

Set V Od samoglasnikov v španščini je podskupina kompleta:

V ⊂ Ñ Zato je končni komplet.

Končni komplet V Iztegnjen način je napisan tako: V = a, e, i, o, u in njegova kardinalnost je 5.

Nabori je mogoče izraziti z razumevanjem. Set F Primer je sestavljen iz črk besede "končni":

F = x / x je črka besede "končni"

Ta komplet, ki je bil izrazit, bo:

F = f, i, n, t, o, katere kardinalnost je 5, zato je končni niz.

Več primerov

Barve mavrice je še en končni primer, komplet C teh barv je:

C = rdeča, oranžna, rumena, zelena, cian, modra, vijolična in njegova kardinalnost je 7.

Nabor faz F Z lune je še en končni primer:

F = Nova luna, rastoča soba, polna luna, padalna soba Ta komplet ima kardinalnost 4.

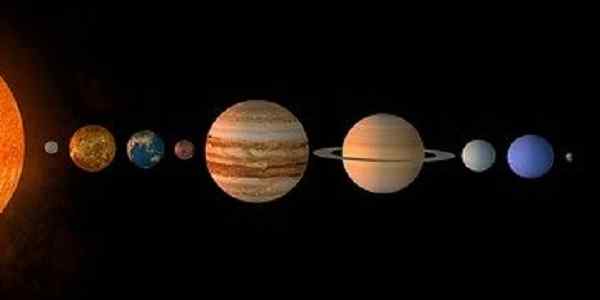Slika 2. Planeti sončnega sistema tvorijo končni komplet. (Pixabay)

Še en končni niz je tisti, ki ga tvorijo planeti sončnega sistema:

P = Merkur, Venera, Zemlja, Mars, Jupiter, Saturn, Uran, Neptun, Pluton kardinalnost 9.

Rešene vaje

Vaja 1

Naslednji niz je podan a = x∊ r / x^3 = 27. Izrazite z besedami in ga napišite po razširitvi, navedite svojo kardinalnost in povejte, ali je končna ali ne.

Vam lahko služi: elipse

Rešitev: Set A je nabor resničnih številk x, tako da je x dvignil na kocko kot rezultat 27.

Enačba x^3 = 27 ima tri rešitve: ki so x1 = 3, x2 = (-3/2 + 3√3/2 i) in x3 = (-3/2-3√3/2 i). Od treh rešitev je samo x1 resničen, druga dva pa zapletena številka.

Ker definicija Set A pravi, da X pripada realnim številom, zato rešitve v zapletenih številkah niso del nabora.

Razširjeni niz je:

A = 3, ki je končni niz kardinalnosti 1.

Vaja 2

Napišite simbolično (z razumevanjem) in obsežno nabor B realnih števil, ki so večje od 0 (nič) in manj ali enake od 0 (nič). Navedite svojo kardinalnost in ali je končna ali ne.

Rešitev: B = x∊ r / 0 < x <= 0

Set B je prazen, ker resnično število X ne more biti hkrati večje in manj kot nič, pa tudi 0 in tudi manj kot 0.

B = in njegova kardinalnost je 0. Prazen komplet je končni komplet.

Vaja 3

Nabor je nabor rešitev določene enačbe. Nabor z razumevanjem je napisan tako:

S = x∊ r / (x -3) (x^2 - 9x + 20) = 0

Ta nabor veliko napišite, navedite svojo kardinalnost in navedite, ali gre za končni niz ali ne.

Rešitev: Prvič, z analizo izraza, ki opisuje niz S, je pridobljeno, da gre za nabor resničnih vrednosti X, ki so rešitve enačbe:

(x -3) (x^2 - 9x + 20) = 0 (*)

Rešitev te enačbe je x = 3, kar je resnično število in zato spada v S. Obstaja pa več rešitev, ki jih je mogoče pridobiti v iskanju rešitev kvadratne enačbe:

Vam lahko služi: porazdelitev F: Značilnosti in vaje rešene

(x^2 - 9x + 20) = 0

Prejšnji izraz lahko upošteva na naslednji način:

(x - 4) (x - 5) = 0

Kar nas vodi do dveh rešitev izvirne (*) enačbe, ki sta x = 4 in x = 5. Skratka, enačba (*) ima rešitve 3, 4 in 5.

S nizom, ki je bil izrazito izražen, je takšen:

S = 3, 4, 5, ki ima kardinalnost 3 in je zato končni niz.

Vaja 4

Obstajata dva niza A = 1, 5, 7, 9, 11 in b = x ∊ n / x je par ^ x x < 10 .

Izrecno napišite set B in poiščite zvezo z nizom a. Poiščite tudi prestrezanje teh dveh sklopov in zaključite.

Rešitev: Set B je sestavljen iz naravnih števil, tako da so enakomerni in so tudi nižji od vrednosti 10, zato je skupaj B široko zapisano na naslednji način:

B = 2, 4, 6, 8

Zveza Set A s setom B je:

A u b = 1, 2, 4, 5, 6, 7, 8, 9, 11

In prestrezanje Set A s setom B je napisano tako:

A ⋂ b = = Ø je prazen niz. 

Treba je opozoriti, da zveza in prestrezanje teh dveh končnih sklopov vodita do novih sklopov, ki so posledično tudi končni.

Reference

1. Viri, a. (2016). Osnovna matematika. Uvod v izračun. Lulu.com.
2. Garo, m. (2014). Matematika: kvadratne enačbe: Kako reševanje kvadratne enačbe. Marilù Garo.
3. Haeussler, npr. F., & Paul, r. S. (2003). Matematika za upravo in ekonomijo. Pearson Education.
4. Jiménez, J., Rodríguez, m., Estrada, r. (2005). Matematika 1 sep. Prag.
5. Dragoceno, c. T. (2005). Tečaj matematike 3o. Uredništvo Progreso.
6. Matematika 10 (2018). "Primeri končnih nizov". Pridobljeno iz: matematika10.mreža
7. Rock, n. M. (2006). Algebra I je enostavna! Tako enostavno. Team Rock Press.
8. Sullivan, J. (2006). Algebra in trigonometrija. Pearson Education.
9. Wikipedija. Končni komplet. Okrevano od: je.Wikipedija.com