Verjetne vrste Aksiomov, razlaga, primeri, vaje

The Aksiomi verjetnost Gre za matematične predloge glede teorije verjetnosti, ki ne zaslužijo demonstracije. Aksiome je leta 1933 ustanovil ruski matematik Andrei Kolmogorov (1903-1987) Osnove teorije verjetnosti in postavil osnovo matematičnega študija verjetnosti.

Pri izvajanju določenega naključnega poskusa ξ je prostor vzorca tisti, ki skupaj z vsemi možnimi rezultati poskusa, imenovan tudi imenovan dogodki. Vsak dogodek je označen kot a in p (a) je verjetnost, da se zgodi. Potem je Kolmogorov ugotovil, da:

Slika 1. Aksiomi verjetnosti omogočajo izračun verjetnosti udarcev na srečo, kot je ruleta. Vir: Pixabay.

-Axiom 1 (brez negativnosti): Verjetnost, da se kateri koli dogodek zgodi, je vedno pozitivna ali nič, P (a) ≥0. Ko je verjetnost dogodka 0, se imenuje Nemogoč dogodek.

-Axiom 2 (gotovost): pod pogojem, da je kakšen dogodek, ki pripada E, njegova verjetnost pojavljanja 1, ki jo lahko izrazimo kot P (e) = 1. Je tisto, kar je znano kot a Varen dogodek, Ker pri izvajanju poskusa obstaja rezultat z vsemi gotovostjo.

-Axiom 3 (dodatek): V primeru dveh ali več nezdružljivih dogodkov dva do dva, poklicana₁, Do₂, Do₃..., verjetnost dogodka₁ več a₂ več a₃ In tako naprej, vsota verjetnosti, da se vsaka zgodi ločeno.

To je izraženo kot: P (a₁ U a₂ U a₃ U ...) = p (a₁) + P (a₂) + P (a₃) +..

Slika 2. Izjemen ruski matematik Andrei Kolmogorov (1903-1987), ki je postavil temelje za aksiomatično verjetnost. Vir: Wikimedia Commons.

[TOC]

Primer

Aksiomi verjetnosti se pogosto uporabljajo v številnih aplikacijah. Na primer:

Klav ali tahuela se vrže v zrak, in ko tla pada, obstaja možnost padca z konico navzgor ali z konico navzdol (d) (ne bomo upoštevali drugih možnosti). Vzorčni prostor tega eksperimenta je sestavljen iz teh dogodkov, potem e = u, d.

Vam lahko služi: revolucijske trdne snovi: volumen, vrste, rešene vajeSlika 3. V poskusu izstrelitve Tachuele obstajata dva dogodka različnih verjetnosti: padec z vrhom ali na tla. Vir: Pixabay.

Z uporabo aksiomov imamo:

P (e) = 1 (Axiom 2)

Ampak P (e) = p (u) + p (d) (Axioma 3), ker so ti dogodki vzajemno nezdružljivi ali ločeni. Hrošč ne pade z vrhom navzgor ali navzdol, hkrati pa je eno ali drugo, vendar ne oboje, saj se upoštevajo druge možnosti. Tako:

P (u) + p (d) = 1

P (u) = 1 - p (d)

Če je enako verjetno padlo z konico navzgor ali navzdol, P (u) = p (d) = ½ (Axiom 1). Lahko pa je, da je zaradi gradnje in zasnove hroščev. Na primer, morda je to P (u) = ¾ medtem P (d) = ¼ (Axiom 1).

Upoštevajte, da v obeh primerih vsota verjetnosti daje 1. Vendar aksiomi ne kažejo, kako dodeliti verjetnosti, vsaj ne v celoti. Vendar potrjujejo, da gre za številke med 0 in 1 in da je, kot se v tem primeru zgodi, vsota vseh 1.

Načine za dodelitev verjetnosti

Aksiomi verjetnosti ne predstavljajo metode dodelitve vrednosti verjetnosti. Za to obstajajo tri možnosti, ki so združljive z aksiomi:

Pravilo Laplace

Vsak dogodek je dodeljen enaka verjetnost, da se zgodi, potem je verjetnost pojava opredeljena kot:

P (a) = število primerov, ki so naklonjeni dogodku A/ število možnih primerov

Na primer, kakšna je verjetnost pridobivanja asa z krova francoskih kartic? Na krovu je 52 kart, 13 od vsake palice in na voljo so 4 palice. Vsaka palica ima 1 kot, tako da je skupno 4 aces:

P (as) = ​​4/52 = 1/13

Pravilo Laplacea je omejeno na končne vzorčne prostore, kjer je vsak dogodek enako verjeten.

Vam lahko služi: diskretna matematika

Relativna frekvenca

Tu mora biti poskus ponovljiv, saj metoda temelji na izvajanju velikega števila ponovitev.

Naredimo ponovitve eksperimenta ξ, od katerih ugotovimo, da je n že tolikokrat, ki se zgodi določen dogodek A, potem je verjetnost, da se bo ta dogodek zgodil:

P (a) = lim_{I → ∞} (Niti)

Kjer je n/i relativna frekvenca dogodka.

Na ta način definirajte P (a) Aksiome Kolmogorov, vendar ima neprijetnosti, da je treba opraviti veliko testov, tako da je verjetnost primerna.

Subjektivna metoda

Oseba ali skupina ljudi se lahko strinja, da bo verjetnost dodelila dogodku z lastnimi presojami. Ta metoda ima pomanjkljivost, da lahko različni ljudje istemu dogodku dodelijo različne verjetnosti.

Vaja rešena

V poskusu hkratnega lansiranja 3 poštenih valut in pridobivanja možnosti za opisane dogodke:

a) 2 obraza in križ.

b) 1 obraz in dva križe

c) 3 križi.

d) vsaj 1 obraz.

Rešitev

Obrazi so označeni s C in križi z x. Vendar obstaja več načinov, kako pridobiti dva obraza in križ. Na primer, prva dva kovanca lahko padeta z obrazom, tretji pa s Cruzom. Ali pa lahko prvi pade obraz, drugi križ in tretji obraz. In končno je prvi lahko križ in preostali obrazi.

Če želite odgovoriti na vprašanja, je treba vedeti vse možnosti, ki so opisane v orodju z imenom Diagram drevesa tudi Drevo verjetnosti:

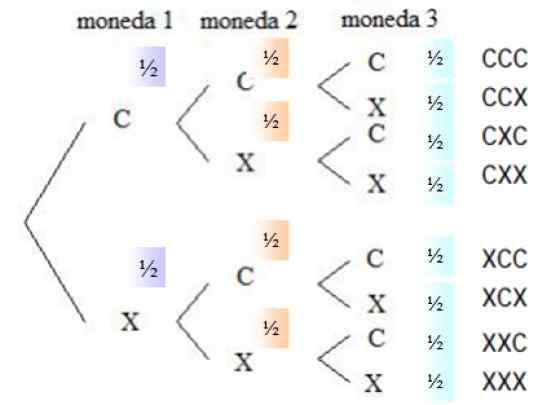Slika 4. Drevesni diagram za hkratno lansiranje treh poštenih kovancev. Vir: f. Zapata.

Verjetnost, da je v kateri koli valuti draga, je ½, enako se zgodi za križe, saj je valuta poštena. V desnem stolpcu so navedene vse možnosti zagona, to je vzorčni prostor.

Vam lahko služi: statistične spremenljivke

Kombinacije, ki se odzovejo na zahtevani dogodek, so izbrane iz vzorčnega prostora, saj vrstni red, v katerem se obrazi pojavljajo, ni pomemben. Obstajajo trije ugodni dogodki: CCX, CXC in XCC. Verjetnost vsakega dogodka je:

P (ccx) = ½. ½ . ½ = 1/8

Enako se zgodi pri dogodkih CXC in XCC, vsak ima 1/8 verjetnost, da se bo zgodilo. Zato je verjetnost pridobitve točno 2 obraza vsota verjetnosti vseh ugodnih dogodkov:

P (2 obraza) = 1/8 + 1/8 + 1/8 = 3/8 = 0.375

Rešitev b

Ugotovitev verjetnosti, da obstajata natanko dva križe, je analogen problem s prejšnjim, iz vzorčnega prostora so vzeti tudi trije ugodni dogodki: CXX, XCX in XXC. Zato:

P (2 križ) = 3/8 = 0.375

Rešitev c

Intuitivno vedo, da je verjetnost pridobivanja 3 križev (ali 3 obrazov) nižja. V tem primeru je iskani dogodek XXX na koncu desnega stolpca, katerega verjetnost je:

P (xxx) = ½. ½. ½ = 1/8 = 0.125.

Rešitev d

Zahteva se, da pridobite vsaj 1 obraz, to pomeni, da lahko zapustijo 3 obraze, 2 obraza ali 1 obraz. Edini dogodek, ki ni združljiv s tem, je tisti, v katerem se pojavijo 3 križi, katerih verjetnost je 0.125. Zato je iskana verjetnost:

P (vsaj 1 obraz) = 1 - 0.125 = 0.875.

Reference

1. Canavos, g. 1988. Verjetnost in statistika: aplikacije in metode. McGraw Hill.
2. Devore, j. 2012. Verjetnost in statistika za inženirstvo in znanost. 8. Izdaja. Cengage.
3. Lipschutz, s. 1991. Serija Schauma: verjetnost. McGraw Hill.
4. Obregón, i. 1989.Teorija verjetnosti. Uredništvo Limusa.
5. Walpole, r. 2007. Verjetnost in statistika za inženirstvo in znanost. Pearson.