Opredelitev curtoze, vrste, formule, za kaj je na primer

The Curtoza ali kurtoza Gre za statistični parameter, ki služi za karakterizacijo verjetnostne porazdelitve naključne spremenljivke, kar kaže na stopnjo koncentracije vrednosti okoli osrednjega ukrepa. To je znano tudi kot "vrhunska ocena".

Izraz izhaja iz grškega "kurtosa", kar pomeni obokano, zato curtoza kaže na stopnjo kazalca ali sploščenja porazdelitve, kot je razvidno iz naslednje slike:

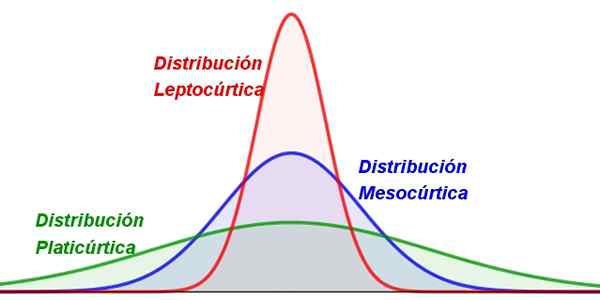Slika 1. Različne vrste curtoze. Vir: f. Zapata.

Skoraj vse vrednosti naključne spremenljivke se ponavadi združijo okoli osrednje vrednosti, kot je povprečje. Toda v nekaterih distribucijah so vrednosti bolj razpršene kot pri drugih, kar ima za posledico bolj sploščene ali bolj vitke krivulje.

[TOC]

Opredelitev

Curtosis je številčna vrednost vsake frekvenčne porazdelitve, ki je glede na koncentracijo vrednosti okoli povprečja razvrščena v tri skupine:

-Leptocuric: v katerem so vrednosti zelo razvrščene okoli povprečja, zato je porazdelitev precej poudarjena in vitka (slika 1, levo).

-Mezocuric: Ima zmerno koncentracijo vrednosti približno v povprečju (slika 1 v središču).

-Filikurično: Ta porazdelitev ima širšo obliko, ker so vrednosti bolj raztresene (slika 1 na desni).

Formule in enačbe

Curtosis ima lahko kakršno koli vrednost, brez omejitev. Njegov izračun se izvaja, odvisno od načina dostave podatkov. Zapis, uporabljen v vsakem primeru, je naslednji:

-Koeficient kortoze: g₂

-Aritmetično povprečje: X ali x s palico

-I-EME: x_Yo

-Standardni odklon: σ

-Število podatkov: N

-Pogostost I-esimo: F_Yo

-Blagovna znamka razreda: mx_Yo

S to notacijo predstavljamo nekaj najpogosteje uporabljenih formul za iskanje curtoze:

Vam lahko služi: vektorski prostor: baza in dimenzija, aksiomi, lastnosti

- Curtoza v skladu s predstavitvijo podatkov

Brez združevanja ali razvrščenih podatkov na frekvencah

Podatki, razvrščeni v presledkih

Presežek curtoze

Tudi poklican Fisherjev koeficient kazalca tudi Fisherjev ukrep, Služi za primerjavo distribucije, ki se preučuje z normalno porazdelitvijo.

Ko je presežna curtoza vredna 0, smo v prisotnosti normalne porazdelitve ali Gauss Bell. Na ta način, dokler se izračuna presežek stroja porazdelitve, ga dejansko primerjamo z normalno porazdelitvijo.

Tako za podatke brez združevanja in za združene podatke je koeficient kazalca Fisherja, označen s K,:

K = g₂ - 3

Vendar je mogoče dokazati, da je curtoza normalne porazdelitve 3, torej če je Fisherjev koeficient kazalca 0 ali blizu 0 in je mezokurična porazdelitev. Če je K> 0 porazdelitev leptokurična in če je K<0 es platicúrtica.

Za kaj je curtoza?

Curtosis je merilo spremenljivosti, ki se uporablja za karakterizacijo morfologije porazdelitve. Na ta način lahko simetrične porazdelitve primerjamo z enakim povprečjem in enako razpršenostjo (ki ga daje standardni odklon).

Ukrepi spremenljivosti zagotavljajo, da so povprečna vrednost zanesljiva in pomaga nadzorovati spremembe distribucije. Kot primer analiziramo ta dva situacija.

3 plače oddelkov

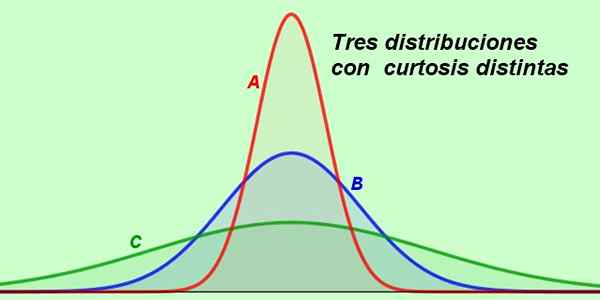
Recimo, da naslednji graf prikazuje porazdelitve v plači 3 oddelkov istega podjetja:

Slika 2. Tri različne porazdelitve ponazarjajo praktične situacije. (Pripravila Fanny Zapata)

Krivulja A je najbolj vitka od vseh, v njegovi obliki.

Vam lahko služi: cele številke

Zaradi dela v oddelku B krivulja plače sledi normalni porazdelitvi, saj je krivulja mezokurična, v kateri domnevamo, da so bile plače naključno porazdeljene.

In končno imamo C krivuljo, ki je zelo sploščena, znak, da je v tem oddelku območje plač veliko širše kot pri drugih.

Rezultati izpita

Recimo, da tri krivulje slike 2 predstavljajo rezultate izpita, ki se uporabljajo za tri skupine študentov istega predmeta.

Skupina, katere kvalifikacije je zastopana z krivuljo do leptokuric, je precej homogena, najbolj dobila povprečno ali tesno oceno.

Možno je tudi, da je bil rezultat posledica dejstva, da so imela izpitna vprašanja bolj ali manj enako stopnjo težav.

Po drugi strani rezultati skupine C kažejo na večjo heterogenost v skupini, ki verjetno vsebuje povprečne študente, še nekaj izjemnih študentov in zagotovo še en manj pozorno.

Ali pa bi lahko pomenilo, da so imela vprašanja testa zelo različne stopnje težav.

Krivulja B je mezokurna, kar kaže na to, da so rezultati testov sledili normalni porazdelitvi. To je običajno najpogostejši primer.

Rešen primer curtoze

Poiščite Fisherjev koeficient za naslednje ocene, pridobljeno v fizičnem izpitu skupini študentov, z lestvico od 1 do 10:

5, 5, 4, 7, 7,7, 9, 8, 9, 4, 3

Rešitev

Naslednji izraz se bo uporabljal za ne -združene podatke, ki so navedeni v prejšnjih razdelkih:

S koeficientom Fisher Point, ki ga daje:

Vam lahko služi: pitagorejske identitete: demonstracija, primer, vaje

K = g₂ - 3

Ta vrednost omogoča poznavanje vrste distribucije.

Za izračun g₂ To je primerno, korak za korakom, saj je treba rešiti več aritmetičnih operacij.

Korak 1

Najprej se izračuna povprečje kvalifikacij. Obstaja n = 11 podatkov.

X = (5+5+4+7+7+7+9+8+9+4+3)/11 = 6.182

2. korak

Najdeno je standardni odklon, za katerega se uporablja ta enačba:

 Z uporabo kalkulatorja s statističnimi funkcijami je rezultat takojšen:

σ = 1.992

Lahko pa sestavite tudi tabelo, ki je potrebna tudi za naslednji korak in v kateri je napisan vsak izraz povzetkov, začenši z (x_Yo - X), potem (x_Yo - X)² In potem (x_Yo - X)⁴ :

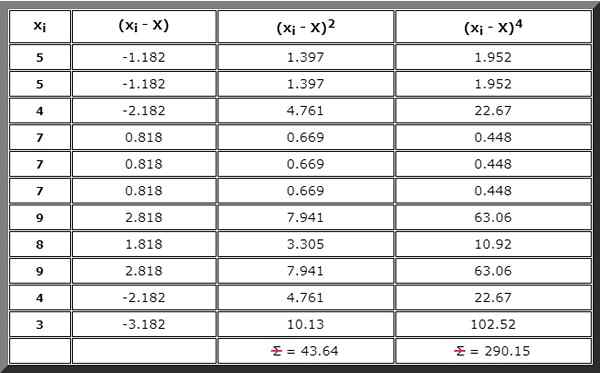
Korak 3

Izvedite vsoto, navedeno v števcu formule za G₂. Za to se uporablja rezultat desnega stolpca prejšnje tabele:

∑ (x_Yo - X)⁴= 290.petnajst

Zato:

g₂ = (1/11) x 290.15 /1.992⁴ = 1.675

Fisherjev koeficient znakov je:

K = g₂ - 3 = 1.675 - 3 = -1.325

Kar zanima, je znak rezultata, ki, kadar negativen, ustreza platoudu različnih stopenj težav.

Uporaba preglednice, kot je Excel, močno olajša ločljivost teh vrst težav in ponuja tudi možnost grafice distribucije.

Reference

1. Levin, r. 1988. Statistika za skrbnike. 2. mesto. Izdaja. Dvorana Prentice.
2. Marco, f. Curtoza. Okrevano od: Economipedia.com.
3. Oliva, J. Asimetrija in curtoza. Pridobljeno iz: StatisticSAUCV.Datoteke.WordPress.com.
4. Spurr, w. 1982. Odločanje v administraciji. Limusa.
5. Wikipedija. Kurtoza. Pridobljeno iz: v.Wikipedija.org.