Podatki niso razvrščeni primeri in rešeni vaja

The Podatki, ki niso združeni To so tisti, ki jih pridobljeni iz študije še niso organizirani po razredih. Kadar gre za obvladljivo število podatkov, običajno 20 ali manj, in malo je različnih podatkov, jih je mogoče obravnavati kot razvrščene in iz njih izvleči dragocene informacije.

Podatki, ki niso združeni, prihajajo iz ankete ali študije, izvedene za njihovo pridobitev, zato nimajo obdelave. Poglejmo nekaj primerov:

Slika 1. Podatki, ki niso združeni, izvirajo neposredno iz katere koli študije in niso bili razvrščeni. Vir: pxhere.

-Rezultati izpita intelektualnega koeficienta na 20 naključnih študentov z univerze. Pridobljeni podatki so bili naslednji:

119, 109, 124, 119, 106, 112, 112, 112, 112, 109, 112, 124, 109, 109, 109, 106, 124, 112, 112,106

-Starost od 20 zaposlenih v zelo priljubljeni kavarni:

24, 20, 22, 19, 18, 27, 25, 19, 27, 18, 21, 22, 23, 19, 22, 27, 29, 23, 20

-Povprečne končne opombe 10 učencev matematičnega razreda:

3.2; 3.1; 2,4; 4.0; 3.5; 3.0; 3.5; 3.8; 4.2; 4.9

[TOC]

Lastnosti podatkov

Obstajajo tri pomembne lastnosti, ki označujejo nabor statističnih podatkov, ki so razvrščene ali ne, ki so:

-Položaj, ki je težnja podatkov, ki jih je treba razvrstiti okoli določenih vrednosti.

-Disperzija, Kaže, kako razpršeni ali razširjeni so podatki o določeni vrednosti.

-Oblika, Se nanaša na način porazdelitve podatkov, kar je razvidno, ko je graf izdelane. Obstajajo zelo simetrične in tudi pristranske krivulje, bodisi na levi bodisi na desni strani določene osrednje vrednosti.

Za vsako od teh lastnosti obstaja več ukrepov, ki jih opisujejo. Ko smo pridobljeni, nam dajo panoramo vedenja podatkov:

-Najbolj uporabljeni položajni ukrepi so aritmetična srednja ali preprosto srednja, srednja in modna.

-V disperziji se območje pogosto uporabljata varianca in standardni odklon, vendar niso edini disperzijski ukrepi.

Vam lahko služi: homotecia

-In za določitev oblike se povprečje in mediana primerjata s pristranskostjo, kot bo kmalu razvidno.

Izračun povprečnega, mediana in mode

-Aritmetična srednja, Znan tudi kot povprečno in označen kot X, izračuna se na naslednji način:

X = (x₁ + x₂ + x₃ +... x_n) / n

Kjer x₁, x₂,.. . x_n, so podatki in n jih je skupno. Če povzamemo vsoto, obstaja:

Tu indeks I predstavlja podatke 1, podatke 2, podatke 3 in tako naprej, dokler ne doseže edinega, ki je zadnji.

-Mediana To je vrednost, ki se pojavi sredi urejenega nasledstva podatkov, zato je za pridobitev podatkov treba najprej naročiti podatke.

Če je število opazovanj čudno, ni težav pri iskanju sredine nabora, če pa imamo par podatkov.

-Moda Je najpogostejša vrednost, ki jo opazimo v naboru podatkov. Ne obstaja vedno, saj je možno, da se nobena vrednost ne ponavlja pogosteje kot druga. Obstajata lahko tudi dva podatkov z enako frekvenco, v tem primeru pa se govori o dvo-modalni porazdelitvi.

Za razliko od prejšnjih dveh ukrepov se moda lahko uporablja s kvalitativnimi podatki.

Poglejmo, kako se izračunajo ti ukrepi položaja s primerom:

Rešen primer

Recimo, da želite določiti aritmetično povprečje, srednje in modo v primeru, predlaganem na začetku: starost od 20 zaposlenih v kavarni:

24, 20, 22, 19, 18, 27, 25, 19, 27, 18, 21, 22, 23, 19, 22, 27, 29, 23, 20

The polovica Izračuna se preprosto z dodajanjem vseh vrednosti in delitvijo z n = 20, kar je skupno število podatkov. Na ta način:

Vam lahko služi: odnosi s sorazmernostjo: koncept, primeri in vaje

X = (24 + 20 + 22 + 19 + 18 + 27+ 25 + 19 + 27 + 18 + 21 + 22 + 23 + 21+ 19 + 22 + 27+ 29 + 23+ 20) / 20 =

= 22.3 leta.

Najti mediana Najprej je treba naročiti nabor podatkov:

18, 18, 19, 19, 19, 20, 20, 21, 21, 22, 22, 22, 23, 23, 24, 25, 27, 27, 27, 29

Kot je nekaj podatkov, se odvzameta dva osrednja podatkov, ki sta izpostavljena krepko, v povprečju. Ker sta oba 22 let, je mediana 22 let.

Končno, moda Dejstvo je, da se najbolj ponavlja ali da je čigava frekvenca večja, saj je ta 22 let.

Razpon, odstopanje, standardni odklon in pristranskost

Obseg je preprosto razlika med glavnimi in najmanj podatki in omogoča, da njihova spremenljivost hitro ceni. Toda razen drugih disperzijskih ukrepov, ki ponujajo več informacij o distribuciji podatkov.

Odstopanje in standardni odklon

Varianta je označena kot S in se izračuna z izrazom:

Pogosto se obdeluje s kvazirianco namesto variance, ki se izračuna na enak način, le razdeljen z N-1, namesto da bi delal med n:

Ker je varianta vsota kvadratov, ima za posledico kvadrat vzorčne enote. Na primer, v študiji starosti zaposlenih v kavarni bi bila varianca prišla čez leta².

Nato je določeno pravilno razlagati rezultate, določeno je standardni odklon, kot je kvadratni koren variance, ali tudi standardna kvazi devijacija, ki je kvadratni koren kvazivariance:

Pristranskost

To je primerjava med povprečnim X in srednjim Med:

-Da med = mediji x: podatki so simetrični.

-Ko x> med: pristransko na desno.

-In če x < Med: los datos sesgan hacia la izquierda.

Vaja rešena

Poiščite povprečno, mediano, modo, rango, odstopanje, standardni odklon in pristranskost za rezultate intelektualnega koeficienta izpita 20 študentov z univerze:

Vam lahko služi: matematične funkcije

119, 109, 124, 119, 106, 112, 112, 112, 112, 109, 112, 124, 109, 109, 109, 106, 124, 112, 112, 106

Rešitev

Naročili bomo podatke, saj bo treba najti mediano.

106, 106, 106, 109, 109, 109, 109, 109, 112, 112, 112, 112, 112, 112, 119, 119, 124, 124, 124

In postavili jih bomo v mizo na naslednji način, da bi olajšali izračune. Drugi stolpec z naslovom "Nabrano" je vsota ustreznih podatkov plus prejšnji.

Ta stolpec bo zlahka našel povprečje in tako delil zadnje nabrano med skupnim številom podatkov, kot je razvidno na koncu stolpca "Akumulirano":

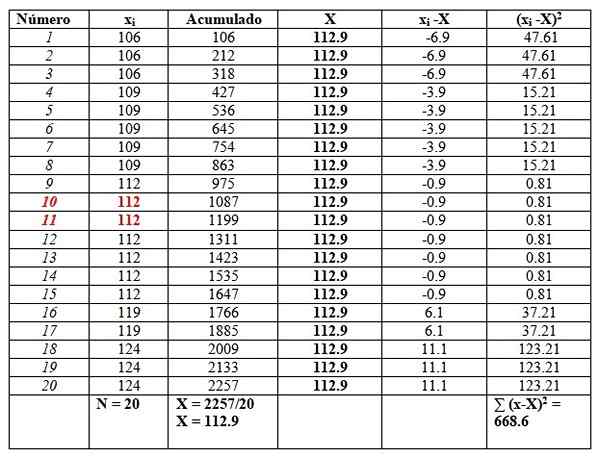
X = 112.9

Mediana je povprečje osrednjih podatkov, poudarjenih v rdeči barvi: številka 10 in številka 11. Kot so enake, je mediana 112.

Končno je moda najbolj ponovljena in je 112, s 7 ponovitvami.

Kar zadeva disperzijske ukrepe, je razpon:

124-106 = 18.

Variance dobimo z deljenjem končnega rezultata desnega stolpca med n:

S = 668.6/20 = 33.42

V tem primeru je standardni odklon kvadratni koren variance: √33.42 = 5.8.

Po drugi strani so vrednosti kvazivarijanstva in kvazi standardnega odklona:

s_c= 668.6/19 = 35.2

Standardna kvazi-devizija = √35.2 = 5.9

Končno je pristranskost rahlo v desno, saj povprečno 112.9 je večji od mediane 112.

Reference

1. Berenson, m. 1985. Statistični podatki za upravo in ekonomijo. Interameriški s.Do.
2. Canavos, g. 1988. Verjetnost in statistika: aplikacije in metode. McGraw Hill.
3. Devore, j. 2012. Verjetnost in statistika za inženirstvo in znanost. 8. Izdaja. Cengage.
4. Levin, r. 1988. Statistika za skrbnike. 2. mesto. Izdaja. Dvorana Prentice.
5. Walpole, r. 2007. Verjetnost in statistika za inženirstvo in znanost. Pearson.