Kotna hitrost Povprečna definicija in formule, rešene vaje

The Povprečna kotna hitrost vrtenja je opredeljen kot kota, ki ga zasukate s položajem vektorske časovne enote točke, ki opisuje krožno gibanje. Rezila stropnega ventilatorja (kot je tisti, prikazan na sliki 1), sledite krožnemu gibanju in njegova povprečna kotna hitrost vrtenja se izračuna tako.

Pravila, ki jim sledi rotacijsko gibanje, so na določen način podobna že sorodnikom translacijskega gibanja. Prevožene razdalje je mogoče izmeriti tudi v metrih, vendar kotne velikosti prevzamejo posebno pomembnost, ker močno olajšajo opis gibanja.

Slika 1. Rezila ventilatorja imajo kotno hitrost. Vir: Pixabay

Grške črke se običajno uporabljajo za kotne velikosti in latinske črke za ustrezne linearne magnitude.

[TOC]

Definicija in formule

Slika 2 predstavlja gibanje točke na krožni poti c. Položaj P točke ustreza trenutnemu t in kotni položaj, ki ustreza temu trenutku, je ϕ. 

Od trenutka, ko preteče obdobje ΔT. V tem obdobju je nov položaj točke P 'in kotni položaj se je povečal kot Δϕ.

Slika 2. Krožno gibanje točke. Vir: Self Made

Povprečna kotna hitrost ω je kot prevožen na enoto časa, tako da bo količnik Δϕ/Δt predstavljal povprečno kotno hitrost med trenutki T in T+ΔT:

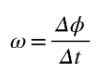
Ker se kot meri v radianih in času v nekaj sekundah, je enotnost povprečne kotne hitrosti rad/s. Če želite izračunati kotna hitrost Ravno takrat t, potem bo treba izračunati količnik Δϕ/Δt, ko bo Δt ➡0.

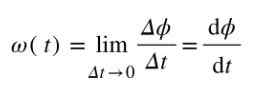Enota merjenja takojšnje kotne hitrosti je tudi rad/s.

Vam lahko služi: 31 vrst sile v fiziki in njihove značilnosti

Enotno vrtenje

Rotacijsko gibanje je enakomerno, če ga kadar koli opazimo, je prevoženi kot enak v istem obdobju. Če je vrtenje enakomerno, potem kotna hitrost kadar koli sovpada s povprečno kotno hitrostjo.

V enotnem rotacijskem gibanju se imenuje čas, v katerem se imenuje popoln zavoj obdobje In je označen s t. 

Poleg tega, ko je prehodni kot poln, je 2π, zato je v enakomerni rotaciji kotna hitrost ω povezana z obdobjem t, po naslednji formuli:

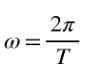
The frekvenca F Enakomerne rotacije, kot je razmerje med številom zavojev in časom, porabljenim za njihovo potovanje, torej v času časov ΔT bo potem frekvenca:

F = n/Δt

Kot krog (n = 1) se prehodi v času t (obdobje), je na voljo naslednje razmerje:

F = 1/t

To pomeni, da je v enotni rotaciji kotna hitrost povezana s frekvenco skozi razmerje:

Ω = 2π ・ f

Razmerje med kotno hitrostjo in linearno hitrostjo

Linearna hitrost v, To je količnik med prevoženo razdaljo in obdobjem, ki se uporablja za potovanje. Na sliki 2 je prevožena razdalja dolžina loka ΔS. 

Lok ΔS je sorazmeren kot prevožen kot Δϕ in radio r, ki izpolnjuje naslednje razmerje:

ΔS = r ・ Δϕ

Kadar koli se meri Δϕ v radianih.

Če razdelimo prejšnji izraz med časovnim obdobjem ΔT, bomo dobili:

(ΔS/ΔT) = r ・ (Δϕ/ΔT)

Prvo razmerje članov je linearna hitrost in količnik drugega člana povprečna kotna hitrost:

Vam lahko postreže: Mount Olympus (Mars)

v = r ・ Ω

Rešene vaje

-Vaja 1

Konice rezil ventilatorja strehe, prikazane na sliki 1, se premikajo s hitrostjo 5 m/s in rezila so 40 cm polmera.

S temi podatki Izračunajte: i) Povprečna kotna hitrost kolesa, ii) Število zavojev, ki jih kolo daje v sekundi, iii) obdobje v sekundah.

Rešitev 

i) linearna hitrost je v = 5 m/s.

Radio je r = 0,40 m.

Iz razmerja med linearno hitrostjo in kotno hitrostjo razčistimo slednje:

v = r ・ ω => ω = v/r = (5 m/s)/(0,40 m) = 12,57 rad/s

ii) ω = 2π ・ f => f = ω / 2π = (12,57 rad / s) / (2π rad) = 2 zavoj / s

iii) t = 1 / f = 1 / (2 zavoj / s) = 0,5 s na krog.

-Vaja 2

Sprehod igrač se premika na krožni progi polmera 2m polmera. Pri 0 je njegov kotni položaj 0 rad, toda po času t je njegov kotni položaj

φ (t) = 2 ・ t .

S temi podatki 

i) Izračunajte povprečno kotno hitrost v naslednjih časovnih intervalih [0S, 0.5s]; [0.5s, 1.0s]; [1.0, 1.5S] in končno v obdobju [0.0, 1.5S]. 

ii) na podlagi rezultatov I), kaj lahko rečemo o gibanju?

iii) Določite povprečno linearno hitrost v istem časovnem obdobju oddelka I)

iv) za vsak trenutek poiščite kotno hitrost in linearno hitrost.

Rešitev 

i) Povprečna kotna hitrost je podana z naslednjo formulo:

Nadaljujemo z izračunom prevoženega kota in obdobje pretečenega v vsakem intervalu.

Interval 1: Δϕ = ϕ (0.5s) - ϕ (0.0S) = 2 (rad/s)*0.5S - 2 (rad/s)*0.0S = 1.0 rad

                   ΔT = 0.5S - 0.0S = 0.5s

Vam lahko služi: BTU (toplotna enota): enakovrednosti, uporabe, primeri

                   Ω = Δϕ/Δt = 1.0rad/0.5s = 2.0 rad/s

Interval 2: Δϕ = ϕ (1.0S) - ϕ (0.5s) = 2 (rad/s)*1.0S - 2 (rad/s)*0.5s = 1.0 rad

                   ΔT = 1.0S - 0.5s = 0.5s

                   Ω = Δϕ/Δt = 1.0rad/0.5s = 2.0 rad/s

Interval 3: Δϕ = ϕ (1.5s) - ϕ (1.0S) = 2 (rad/s)*1.5S - 2 (rad/s)*1.0S = 1.0 rad

                   ΔT = 1.5S - 1.0S = 0.5s

                   Ω = Δϕ/Δt = 1.0rad/0.5s = 2.0 rad/s

Interval 4: Δϕ = ϕ (1.5s) - ϕ (0.0S) = 2 (rad/s)*1.5S - 2 (rad/s)*0.0S = 3.0 rad

                   ΔT = 1.5S - 0.0S = 1.5s

                   Ω = Δϕ/Δt = 3.0rad/1.5s = 2.0 rad/s

ii) Glede na prejšnje rezultate, v katerih je bila v različnih časovnih intervalih izračunana povprečna kotna hitrost, je vedno dosežen isti rezultat. Zdi se, da gre za enotno krožno gibanje. Vendar ti rezultati niso dokončni.

Način, kako zagotoviti zaključek, je izračunati povprečno kotno hitrost za poljubni interval [t, t -t)

                                     ΔT = t ' - t

                                     Ω = Δϕ/Δt = 2*(t'-t)/(t'-t) = 2.0 rad/s

To pomeni, da ima sprehod z igračami konstantno povprečno kotno hitrost 2 rad/s v katerem koli obravnavanem obdobju. Lahko pa greste dlje, če se izračuna takojšnja kotna hitrost:

To se ves čas razlaga kot avtomobil z igračami ima konstantno kotno hitrost = 2 rad/s.

Reference

1. Giancoli, d. Fizika. Načela z aplikacijami. 6. izdaja. Dvorana Prentice. 30-45.
2. Kirkpatrick, l. 2007. Fizika: pogled na svet. 6^ta Skrajšana izdaja. Cengage učenje. 117.
3. Resnick, r. (1999). Fizično. Zvezek 1. Tretja izdaja v španščini. Mehika. Continental uredništvo s.Do. od c.V. 33-52.
4. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7. Izdaja. Mehika. Uredniki učenja Cengage. 32-55.
5. Wikipedija. Kotna hitrost. Okreval od: Wikipedia.com