Relativno gibanje v dimenziji, v dveh dimenzijah

On relativno gibanje delca ali predmeta je tisti, ki ga opazimo glede na določeno referenčno točko, ki jo je izbral opazovalec, ki se lahko fiksira ali premika. Hitrost se vedno nanaša na kakšen koordinatni sistem, ki se uporablja za njegovo opis.

Na primer, Co -pilot premikajočega se avtomobila in ki potuje udobno zaspan na njegovem sedežu, je v mirovanju v mirovanju v zvezi z voznikom, vendar ni za opazovalca, ki stoji na pločniku, ki vidi, da je avtomobil prehoden.

Slika 1. Letala ohranjajo določeno relativno hitrost med njimi pri vadbi akrobacije. Vir: Pixabay.

Potem je gibanje vedno relativno, vendar se zgodi, da je običajno izbran koordinatni ali referenčni sistem, ki ima svoj izvor v zemlji ali tleh, kraj, ki velja za stacionarno mesto. Na ta način se skrb osredotoča na opisovanje gibanja predmeta, ki se preučuje.

Ali je mogoče opisati hitrost spalnega sodelavca glede na potnika, ki potuje v drugem avtomobilu? Odgovor je pritrdilen. Obstaja svoboda izbire vrednosti (x_tudi, in_tudi, z_tudi): Izvor referenčnega sistema. Izbira je poljubna in je odvisna od preferenc opazovalca, pa tudi do enostavnosti, ki jo zagotavljate za reševanje problema.

[TOC]

Relativno gibanje v dimenziji

Ko gibanje prehaja po ravni črti, imajo mobilniki hitrosti v isti smeri ali v nasprotni smeri, oba pa jo vidi opazovalec, ki stoji na kopnem (T). Ali se opazovalec premakne v zvezi z mobilnimi telefoni? Da, z enako hitrostjo, vendar v nasprotni smeri.

Kako se mobilni premik premika glede na drugega? Če želite ugotoviti, se hitrosti dodajo vektor.

Lahko vam služi: Pluton (pritlikavi planet)

-Rešen primer 1

Glede na prikazano sliko navedite relativno hitrost avtomobila 1 glede na avtomobil 2 v vsaki situaciji.

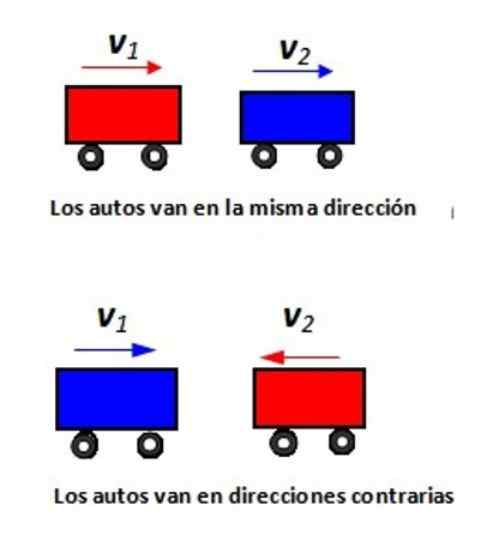Slika 2. Dva avtomobila se odpravita na pravokotno cesto: a) v isti smeri in b) v nasprotni smeri.

Rešitev

Hitrosti bomo dodelili pozitivni znak na desni in negativni znak na levi. Če mobilni telefon gre desno na 80 km/h, potnik v tem mobilnem telefonu vidi opazovalca na tleh, ki se premika na - 80 km/h.

Recimo, da se vse zgodi vzdolž osi x. Na naslednji sliki se rdeči avtomobil premakne na +100 km/h (vidno od T) in se pripravlja na prehod modrega avtomobila, ki potuje na +80 km/h (vidno tudi od T). S kakšno hitrostjo vidite, da potnik pristopi v rdečem avtomobilu v modrem avtomobilu?

Nalepke so: v _1/2 Samodejna 1 hitrost glede na 2, v_1/t Hitrost avtomobila glede na T, v_T/2 Hitrost tabele glede na 2. Dodajanje vektorično:

v_1/2 = v_1/t + v_T/2 = (+100 km/h - 80 km/h) x= 20 km/h x

Lahko brez vektorja. Opomba Naročniki: Pomnoževanje obeh na desni mora pridobiti tisto na levi strani.

In ko so v nasprotni smeri? Zdaj v_1/t = + 80 km/h in V_2/t = -100 km/h, torej v_T/2 = + 100 km/h. Potnik avtomobilske modre bo videl rdeči avtomobil, ki se približuje:

v_{1/2 =} v_1/t + v_T/2 = +80 km/h +100 km/h = 180 km/h

Relativno gibanje v dveh in treh dimenzijah

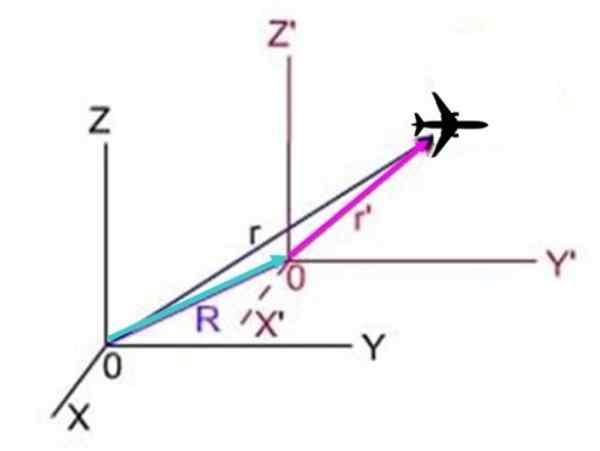
V naslednji shemi, r Je položaj ravnine, ki jo vidimo iz sistema X in z, r'To je položaj iz sistema X in z ' in R To je položaj sistema s premijo glede na sistem brez premije. Trije vektorji tvorijo trikotnik, v katerem R + r'= r, Zato r'= r - r.

Slika 3.- Letalo se premika glede na dva koordinatna sistema, kar se tiče enega od sistemov glede na drugega.

Ker je derivat glede na čas položaja natančno hitrost, rezultati:

Vam lahko služi: parabolični posnetek: značilnosti, formule in enačbe, primeri

v'= v - ali

V tej enačbi v„To je hitrost ravnine glede na sistem X in z ', v je hitrost glede na sistem X in z in ali To je stalna hitrost glavnega sistema glede na sistem brez premij.

-Vaja Rešena 2 

Letalo je v severni smeri s hitrostjo glede na zrak 240 km/h. Kar naenkrat začne pihati veter od zahoda proti vzhodu s hitrostjo 120 km/ po Zemlji.

Poiščite: a) Hitrost ravnine glede na zemljo, b) odstopanje, ki ga je doživel pilot c) popravek, ki ga mora pilot narediti, da lahko usmerite neposredno na sever in novo hitrost glede na kopno, enkrat, enkrat Popravek je bil narejen.

Rešitev

a) Naslednji elementi so: ravnina (a), zemlja (t) in veter (v).

V koordinatnem sistemu, v katerem je sever + in in zahodni vzhod je + x, obstajajo dane hitrosti in njihova nalepka (naročniki):

v _Av = 240 km/h (+in); v _V/t = 120 km/h (+x); v _A/t = ?

Ustrezna vektorska vsota je:

v _A/t = v _Av + v _V/t = 240 km/h (+in) + 120 km/h (+x)

Velikost tega vektorja je: v _A/t = (240 ²+ 120²)^1/2 km/h = 268.3 km/h

b) θ = arctg (v _Av / v _V/t) = ARCTG (240 /120) = 63.4. severno od vzhoda ali 26.6. severovzhod.

c) Če želite nadaljevati na severu s tem vetrom, morate usmeriti lok ravnine na severozahod, tako da ga veter potisne neposredno proti severu. V tem primeru bo hitrost letala, ki jo vidimo od tal, v +in, medtem ko bo hitrost letala glede na veter severozahod (ni nujno 26.6.

Vam lahko služi: teorem Bernoulli

Avtor pitagora teorem:

v _A/t = (240 ²- 120²)^1/2 km/h = 207.8 km/h

α = ARCTG (V _V/t / v _A/t ) = ARCTG (120/207.8) = 30. severozahod

-Vaja rešena 3

Oseba si vzame 2 minuti, da se sprehodi po nepremičnem mehanskem stopnišču. Če stopnišče deluje, si oseba vzame 1 minuto, da se mirno spusti. Kako dolgo se oseba sprehaja in s stopniščem teče?

Rešitev

Upoštevati je treba tri elemente: oseba (p), stopnišče (e) in tla, katerih relativne hitrosti so:

v_P/e : hitrost osebe glede na lestev; v_Je: hitrost stopnišča glede na tla; v_P/s: Hitrost osebe glede na tla.

Kot je od tal razvidno s fiksnim opazovalcem, ima oseba, ki spusti stopnišče (e) _P/s dobiti od:

v _P/s = v_P/e + v_Je

Pozitiven smisel se spušča po stopnicah. Biti t  čas, ki je potreben za hojo in L razdalja. Velikost osebe v _P/s je:

v_P/s = L / t

t₁ Čas je, da se spustite z utrditvijo lestve: V _P/e = L / t₁

In t₂ Tistega, ki vas v gibanju še vedno popelje na stopnišče: V _Je = L / t₂

Kombiniranje izrazov:

L / t = l / t₁ + L / t₂

Zamenjava numeričnih vrednosti in čiščenje t:

1 / t = 1 / t₁ + 1 / t₂ = 1/2 + 1/1 = 1.5

Potem t = 1/1.5 minut = 40 sekund.

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill. 84-88.
2. Figueroa, d. Fizične serije za znanost in inženiring. Zvezek 3. Izdaja. Kinematika. 199-232.
3. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6^th. Ed. Dvorana Prentice. 62-64.
4. Relativno gibanje. Obnovi se od: tečajev.Lumenarning.com
5. Wilson, J. 2011. Fizika 10. Pearson Education. 166-168.