Kaj so vektorji koplanares? (Z rešenimi vajami)

The Koplanares vektorji o Coplanarios so tisti, ki so vsebovani na isti ravnini. Ko imate samo dva vektorja, sta to vedno sklop.

Če imate tri ali več vektorjev, je morda to, da kateri od njih ni v isti ravnini kot drugi, zato jih ne bi mogli šteti za koplanare. Naslednja slika prikazuje nabor koplanares, označenih s krepkimi vektorji Do, B, C in D:

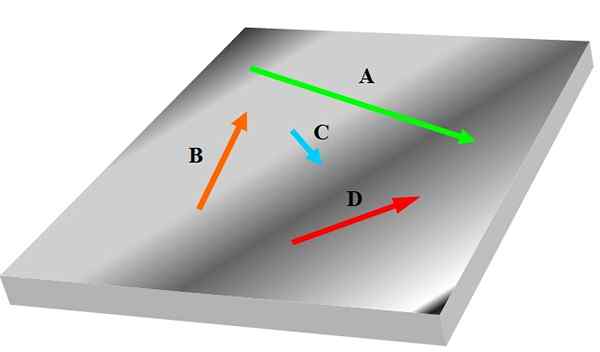Slika 1. Štirje koplanares. Vir: Self Made.

Vektorji so povezani z vedenjem in lastnosti ustreznih fizičnih velikosti v znanosti in inženiringu; na primer hitrost, pospešek in moč.

Sila povzroča različne učinke na predmet, kadar je način uporabe raznolik, na primer spreminjanje intenzivnosti, smeri in pomena. Še vedno spreminjajo enega od teh parametrov, rezultati so bistveno različni.

V mnogih aplikacijah, tako v statični kot dinamiki, so sile, ki delujejo na telesu.

[TOC]

Pogoji, da so vektorji koplanares

Da bi bili trije vektorji koplanares, morajo biti na isti ravnini in to se zgodi, če izpolnjujejo katerega od naslednjih pogojev:

-Vektorji so vzporedni, zato so njihove komponente sorazmerne in so linearno odvisne.

-Vaš mešani izdelek je praznina.

-Če imate tri vektorje in katerega koli od njih lahko zapišete kot linearna kombinacija drugih dveh, so ti vektorji koplanares. Na primer vektor, ki je posledica vsote dveh drugih, so trije v isti ravnini.

Vam lahko služi: voltmeter: značilnosti, delovanje, za kaj je, vrste

Druga možnost je, da se pogoj koplanarnosti določi na naslednji način:

U v w So koplanare, če obstajajo tri številke (skalarji) α, β, γ, tako da αali + βv + γW = 0 Z (α, β, γ), ki se razlikuje od (0, 0, 0)

Mešani izdelek med tremi vektorji

Mešani izdelek med vektorji je definiran s tremi vektorji ali, v in W, kar ima za posledico skalar, ki je posledica izvedbe naslednje operacije:

ali · (v x W) = ali · (v x W)

Najprej je narejen navzkrižni izdelek, ki je v oklepajih: v x W, čigar rezultat je normalen (pravokotni) vektor do ravnine, v kateri so tako v kot W.

Ja ali je na isti ravnini kot v in W, Seveda skalarni izdelek (točkovni izdelek) med U in omenjenim normalnim vektorjem mora biti 0. Na ta način je preverjeno, da so trije vektorji koplanare (ležijo na isti ravnini).

Ko mešani izdelek ni ničen, je njegov rezultat enak volumnu vzporednic, ki ima vektorje ali, v in W kot sosednje strani.

Prijave

Koplanare, sočasne in nekolinealne sile

Prednosti sočasno Vsi so uporabljeni na isti točki. Če so tudi koplanare, jih lahko zamenjate samo z enim, ki se imenuje posledična sila In ima enak učinek kot pri prvotnih silah.

Če je telo v ravnotežju, zahvaljujoč trem koplanarem, sočasnim in ne -kololinealnim (ne -palelskim) silam, imenovanim Do, B in C, on Lamyjev teorem Poudarja, da je odnos med temi silami (magnitudes) naslednji:

A / sin α = b / sen β = c / sen γ

Z α, β in γ kot koti, ki nasprotujejo uporabljenim silam, kot je prikazano na naslednji sliki:

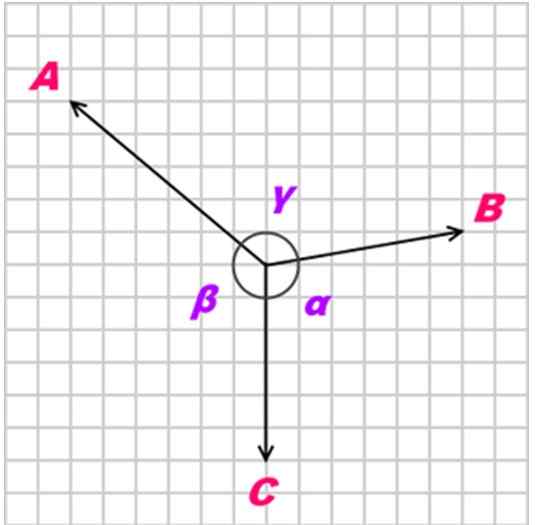Slika 2. Tri sile A, B in C Coplanares delujejo na predmetu. Vir: Kiwakwok v angleški Wikipediji [javna domena]

Rešene vaje

-Vaja 1

Poiščite vrednost K tako, da bodo naslednji vektorji koplanare:

Vam lahko postreže: Carnot Machine

ali =

v =

W =

Rešitev

Ker so sestavni deli vektorjev, se zato uporabljajo kriteriji mešanega izdelka:

ali · (v x W) = 0

Najprej je rešeno v x W. Vektorji bodo izraženi v smislu enotnih vektorjev Yo, J in k ki razlikujejo tri pravokotne smeri v vesolju (široki, visoki in globini):

v= 4 Yo + J + 0 k

W= -1 Yo + 2J -1 k

v x W = -4 (i x i) + 8 (i x j) - 4 (i x k) - (J x i) + 2 (J x J) - 2 (J x k) = 8 k + 4 J + k -2 i = -2 Yo + 4 J + 9 k

Skalarni izdelek je zdaj predlagan med U in vektorjem, ki ima rezultate prejšnjega delovanja, ki ustreza operaciji na 0:

ali · (v x W) = (-3 Yo + k J + 2 k) · (-2 Yo + 4 J + 9 k) = 6 + 4K +18 = 0

24 + 4K = 0

Iskana vrednost je: K = - 6

Tako da vektor ali je:

ali =

-Vaja 2

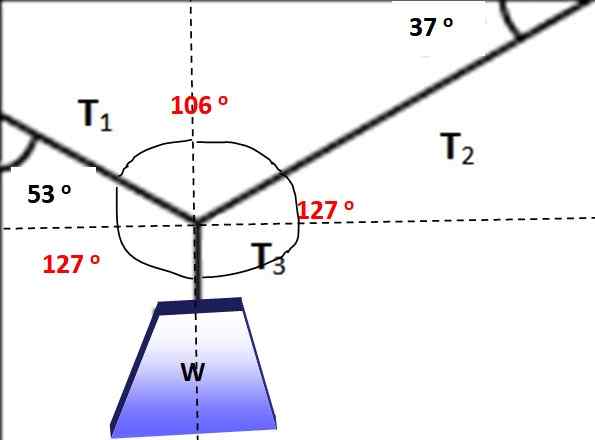
Na sliki je prikazan predmet, katerega teža je w = 600 n, ki visi v ravnovesju, zahvaljujoč kablim, nameščenim v skladu s koti, prikazanimi na sliki 3. Ali je mogoče v tej situaciji uporabiti Lamyjev izrek? V vsakem primeru poiščite veličine T₁, T₂ in T₃ ki omogočajo ravnotežje.

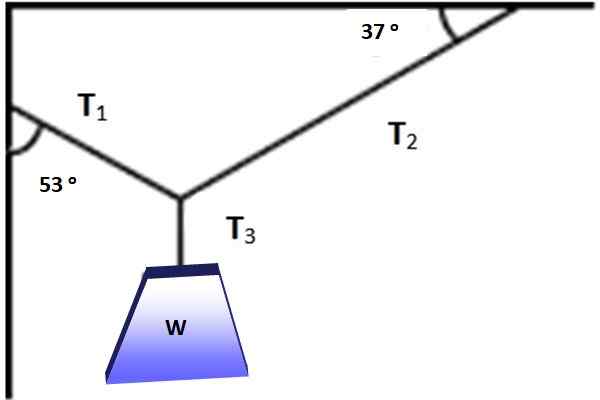Slika 3. Teža visi v ravnovesju pod delovanjem treh prikazanih napetosti. Vir: Self Made.

Rešitev

Lamyjev teorem je v tej situaciji uporaben, če se upošteva vozel, za katerega se uporabljajo tri napetosti, saj predstavljajo sistem koplanarnih sil. Najprej je shemi prostega telesa narejen za obesek, da se določi velikost T_3:

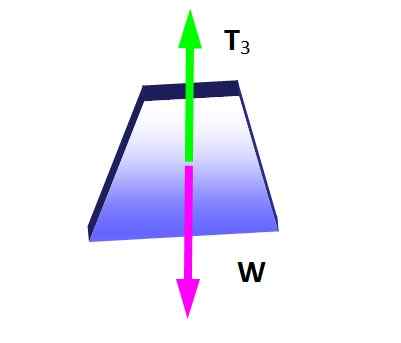Slika 4. Brezplačni karoserijski diagram za visenje teže. Vir: Self Made.

Iz ravnotežnega stanja sledi:

Vam lahko služi: difrakcija zvoka: kaj je, primeri, aplikacije

T₃  = W = 600 n

Koti med silami so na naslednji sliki označeni z rdečo barvo, zlahka preverite, ali je njegova vsota 360 °. Zdaj je mogoče uporabiti Lamyjev izrek, saj je znana ena od sil in trije koti med njimi:

Slika 5.- V rdeči koti za nanašanje lamyjevega izrek. Vir: Self Made.

T₁ / Sen 127 ° = w / sen 106 °

Zato: t₁ = Sen 127 ° (w /sen 106º) = 498.5 n

Spet Lamyjev teorem se uporablja za čiščenje t₂:

T₂ / greh 127 = t₁ / Sen 127 °

T₂ = T₁ = 498.5 n

Reference

1. Figueroa, d. Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika. 31-68.
2. Fizično. Modul 8: Vektorji. Okrevano od: FRTL.UTN.Edu.ar
3. Hibbeler, R. 2006. Mehanika za inženirje. Statična. 6. izdaja. Continental uredništvo.28-66.
4. McLean, w. Serija Schaum. Mehanika za inženirje: statična in dinamična. 3. izdaja. McGraw Hill. 1-15.
5. Wikipedija. Vektor. Okrevano od: je.Wikipedija.org.