Nekoplanarni vektorji Opredelitev, pogoji, vaje

The Ne -koplanares vektorji Oni so tisti, ki nimajo iste ravnine. Dva prosta vektorja in ena točka določata eno samo ravnino. Tretji vektor lahko to letalo ali ne more deliti in če tega ne, so to nekoplanarni vektorji.

Ne -komplet vektorjev ni mogoče predstaviti v dveh vidimenzionalnih prostorih, kot sta deska ali list papirja, ker so nekateri od njih v tretji dimenziji. Če jih želite pravilno predstavljati, morate uporabiti perspektivo.

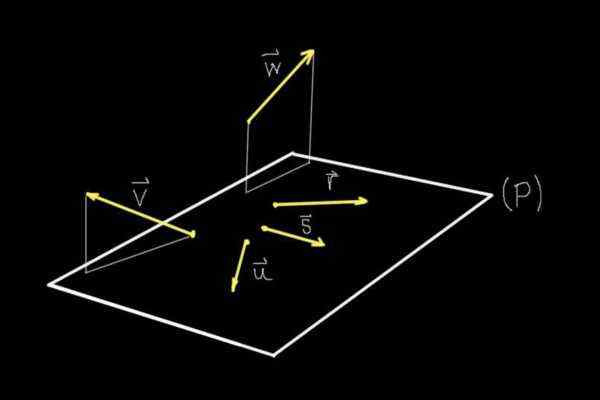Slika 1. Koplanare in vektorje, ki ne spadajo. (Lastna izdelava)

Če opazimo sliko 1, so vsi predmeti, ki so strogo prikazani.

Na tej ravnini (p) so vektorji r, s, ali, medtem ko vektorji v in W  Niso na tem letalu.

Zato vektorji r, s, ali So koplanarioji ali koplanare med seboj, saj imajo isto ravnino (P). Vektorji v in W Ne delijo stanovanja z nobenim od drugih prikazanih vektorjev, zato ne spadajo. 

[TOC]

Vektorji koplanares in ravninske enačbe

Letalo je edinstveno določeno, če so v treh dimenzionalnih prostorih podane tri točke.

Recimo, da so te tri točke bistvo Do, točka B in točka C ki definira ravnino (P). S temi točkami je mogoče zgraditi dva vektorja AB = U in Ac = v ki so z gradnjo z letalom (P).

Vektorski (ali navzkrižni) produkt teh dveh vektorjev povzroči tretji pravokotni (ali normalen) vektor in zato pravokotno na ravnino (P):

n = u X v   => n ⊥ ali  in n ⊥ v   => n ⊥ (P)    

Vam lahko služi: teža (fizična): izračun, enote, primeri, vaje

Katero koli drugo točko, ki spada v letalo (P) mora izpolniti to vektor Aq Bodite pravokotni na vektor n; To je enakovredno temu, da je skalarni izdelek (ali točkovni izdelek) n z Aq Mora biti nič:

n • Aq = 0 (*)

Prejšnji pogoj je enakovreden temu:

Aq • (ali X v) = 0 

Ta enačba zagotavlja, da je točka Q pripadajo letalu (P). 

Kartezijanska enačba letala

Prejšnja enačba je mogoče zapisati na kartezijanski način. Za to napišemo koordinate točk Do, Q in komponente običajnega vektorja n:

A = (a, b, c)

Q = (x, y, z)

n= (NX, NY, NZ)

Tako da so komponente AQ:

Aq= (X-a, y-b, z-c)

Pogoj za vektor Aq vsebovati v ravnini (P) Je pogoj (*), ki je zdaj napisan tako:

(NX, NY, NZ) • (X-A, Y-B, Z-C) = 0

Izračun točkovnega izdelka ostaja:

nx (x-a) + ny (y-b) + nz (z-b) = 0

Če se razvije in preuredi, ostaja:

nx x + ny y + nz z = nx a + ny b + nz c

Prejšnji izraz je kartezijanska enačba ravnine (P), odvisno od sestavnih delov običajnega vektorja (P) in koordinate točke Do ki pripada (P).

Pogoji za tri vektorje, ki niso koplanare

Ker je bil pogoj viden v prejšnjem razdelku Aq • (ali X v) = 0 zagotavlja, da vektor Aq To je Coplanario A ali in v.

Če pokličemo W do vektorja Aq Potem lahko to potrdimo:

W, ali in v So koplanare, da in samo, če W • ( ali X v ) = 0.

Stanje ne-vedenja

Če je trojni (ali mešani izdelek) produkt treh vektorjev drugačen od nič.

Lahko vam služi: Politični postopek: značilnosti, aplikacije in primeri

Ja    W • ( ali X v ) ≠ 0 Nato so vektorji U, V in W ne-kiplanariosi.

Če se kartezijanske komponente U, V, V in W uvedejo, se lahko stanje ne-vedenja zapiše na naslednji način:

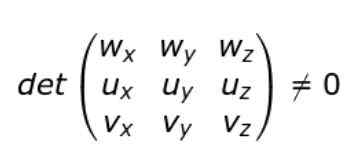To pomeni, da če je determinant matrice (3 × 3), katere vrstice so sestavne dele vektorjev U, V in W, potem vektorji ne.

Trojni izdelek ima geometrijsko razlago in predstavlja glasnost vzporednikov, ki jih ustvarijo trije vektorji, ki niso koplanare.

Slika 2. Trije vektorji, ki ne gredo. (Lastna izdelava)

Razlog je naslednji; Ko se dva vektorje, ki niso povezani, se pomnožijo. 

Potem, ko se ta vektor pomnoži. 

Z drugimi besedami, območje paralelograma, ki ga ustvarita prva dva, pomnožena z višino tretjega vektorja.

Alternativni pogoj nemotenja

Če imate tri vektorje in katerega koli od njih ne morete napisati kot linearna kombinacija drugih dveh, potem so trije vektorji neobjavljeni. To so trije vektorji ali, v in W Če pogoj ne pokrivajo:

α ali + β v + γ W = 0

Izpolnjeno je le, ko je α = 0, β = 0 in γ = 0.

Rešene vaje

-Vaja 1

Imate tri vektorje

ali = (-3, -6, 2);   v = (4, 1, 0) in W = (-1, 2, z)

Upoštevajte, da vektorska komponenta Z W Ni znano.

Poiščite obseg vrednosti, ki jih lahko vzame, tako da je zagotovljeno, da trije vektorji ne delijo iste ravnine.

Vam lahko služi: stabilno ravnovesje: koncept in primeri

Rešitev 

Ponovno uporabimo merilo determinanta matrice, ki ga tvorijo vrsta treh vektorjev, na ta način ostajamo: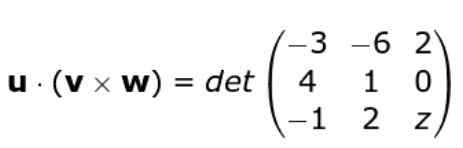Razvijamo determinant

W • ( ali X v ) = -3 (z - 0) + 6 (4 z - 0) + 2 (8 + 1) = -3z + 24Z + 18 = 21z + 18

Ta izraz se ujemamo z ničelno vrednostjo

21 Z + 18 = 0

in razčistimo z

Z = -18/21 = -6/7

Če bi spremenljivka Z vzela vrednost -6/7, bi bili trije vektorji koplanares.

Tako da so vrednosti z, ki zagotavljajo, da so vektorji neporavnani, tiste, ki so v naslednjem intervalu:

Z ∈ (-∞, -6/7) U (-6/7, ∞)

-Vaja 2

Poiščite prostornino paralelepiped, prikazano na naslednji sliki:

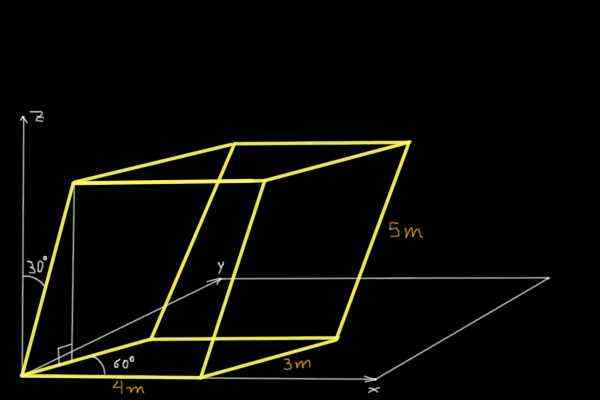
Rešitev 

Če želite najti količino paralelepiped, ki je prikazan na sliki, bodo kartezijanske komponente treh nekonkurtnih ne-sklopnih vektorjev določene v izvoru koordinatnega sistema. Prvi je vektor ali  4m in vzporedno z osi x:

ali= (4, 0, 0) m

Drugi je vektor v V ravnini velikosti XY 3M, ki tvori 60 ° z osi x:

v= (3*cos 60º, 3*sen 60º, 0) = (1.5, 2.6, 0.0) m

In tretji vektor W 5M in katerih projekcija v ravnini XY tvori 60 ° z osi x, poleg tega pa W tvori 30 ° z os z.

W= (5*greh 30 °*cos 60º, 5*sen 30º*greh 60 °, 5*sen 30 °)

Izvedli izračune, ki jih imamo: W= (1.25, 2.17, 2.5m.

Reference

1. Figueroa, d. Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika. 31-68.
2. Fizično. Modul 8: Vektorji. Okrevano od: FRTL.UTN.Edu.ar
3. Hibbeler, R. 2006. Mehanika za inženirje. Statična. 6. izdaja. Continental uredništvo.28-66.
4. McLean, w. Serija Schaum. Mehanika za inženirje: statična in dinamična. 3. izdaja. McGraw Hill. 1-15.
5. Wikipedija. Vektor. Okrevano od: je.Wikipedija.org