Koncept relativne hitrosti, primeri, vaje

The Relativna hitrost predmeta je tisti, ki se meri glede na dani opazovalec, saj lahko drug opazovalec pridobi drugačen ukrep. Hitrost je vedno odvisna od opazovalca, ki ga meri.

Zato bo hitrost predmeta, ki jo meri določena oseba, relativna hitrost glede nanj. Drugi opazovalec lahko pridobi drugačno vrednost za hitrost, še vedno v primeru istega predmeta.

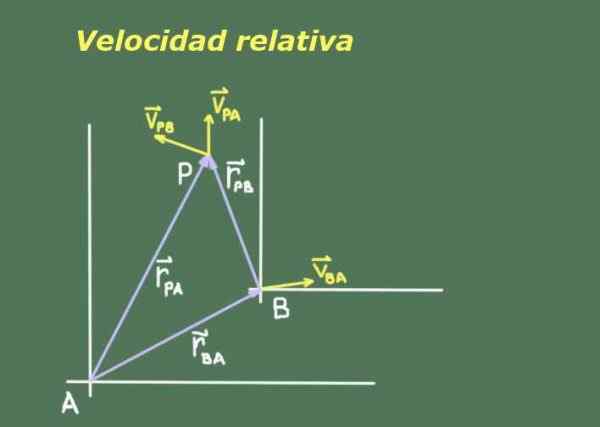
Slika 1. Shema, ki predstavlja točko P v gibanju, ki jo vidimo iz referenčnih sistemov A in B. Vir: Self Made.

Ker imata dva opazovalca A in B, ki se premikata drug od drugega, imata različne ukrepe tretjega P objekta, ki se premika, je treba iskati razmerje med položaji in hitrostmi pogledov P s A in B.

Slika 1 prikazuje dva opazovalca A in B z ustreznimi referenčnimi sistemi, od katerih merita položaj in hitrost predmeta P.

Vsak opazovalec A in B v določenem času meri položaj in hitrost predmeta P t. V klasični relativnosti (ali Galilejci) je čas za opazovalca A enak kot za opazovalca B, ne glede na njegove relativne hitrosti.

Ta članek govori o klasični relativnosti, ki je veljavna in uporabna za večino vsakodnevnih situacij, v katerih imajo predmeti veliko nižje hitrosti kot svetloba.

Položaj opazovalca B glede označevanja kot r_Ba. Ker je položaj vektorski znesek, uporabljamo krepko, da ga označimo. Položaj predmeta P glede na označevanje kot r_Pa in istega predmeta P glede B r_Pb.

[TOC]

Razmerje med položaji in relativnimi hitrostmi

Obstaja vektorsko razmerje med temi tremi stališči, ki jih je mogoče razbrati iz prikazovanja slike 1:

 r_Pa= r_Pb + r_Ba

Če se prejšnji izraz sprejme glede na čas t Dobili bomo razmerje med relativnimi hitrostmi vsakega opazovalca:

Lahko vam služite: Newtonov drugi zakon: aplikacije, poskusi in vaje

V_Pa= V_Pb + V_Ba

V prejšnjem izrazu je relativna hitrost P glede na relativno hitrost P glede na B in relativno hitrost B glede na to.

Podobno lahko relativno hitrost P zapišemo glede na relativno hitrost P glede na A in relativno hitrost B.

V_Pb= V_Pa + V_Ab

Treba je opozoriti, da je relativna hitrost glede na B enaka in v nasprotju s hitrostjo B glede na A:

V_Ab = -V_Ba 

To vidi otrok iz premikajočega se avtomobila

Avto gre po ravni cesti, ki sega od zahoda do tega, hitro od 80 km/h, medtem ko v nasprotni smeri (in na drugem pasu) pride hitro motocikel 100 km/h.

Na zadnjem sedežu avtomobila potuje z otrokom, ki želi vedeti relativno hitrost motocikla, ki se mu približuje. Če želite izvedeti odgovor, bo otrok uporabil odnose, ki ste jih pravkar prebrali v prejšnjem razdelku, in določil vsak koordinatni sistem na naslednji način:

-A je koordinatni sistem opazovalca na cesti in glede nanj so bili izmerjeni rapidi vsakega vozila.

-B je avto in P bo motocikel.

Če želite izračunati hitrost moto p glede na avtomobil B, bo uporabljeno naslednje razmerje:

V_Pb= V_Pa + V_Ab=V_Pa - V_Ba

Kot pozitivno smer, ki jo imate:

V_Pb= (-100 km/h - 80 km/h) Yo = -180 km/h Yo

Ta rezultat se razlaga na naslednji način: Motocikel se premika glede na avtomobil s hitrostjo 180 km/h in smerjo -Yo, to pomeni to na zahodu.

Lahko vam služi: blok algebra: elementi, primeri, rešene vaje

Relativna hitrost med motociklom in avtomobilom

Motocikel in avtomobil sta prečkala vsakega za svoj vozni pas. Fant, ki gre na zadnji sedež avtomobila, vidi motocikel stran in zdaj želi vedeti, kakšno hitrost se oddalji od njega, ob predpostavki.

Če poznate odgovor, otrok uporablja isto razmerje, ki je bil prej uporabljen:

V_Pb= V_Pa + V_Ab=V _Pa - V_Ba

V_Pb= -100 km/h Yo - 80 km/h Yo = -180 km/h Yo

In zdaj se motocikel oddalji od avtomobila z enako relativno hitrostjo, s katero so se približali, preden so prečkali.

Isti motocikel 2. dela se vrne tako, da ohrani enako hitrost 100 km/h, vendar spremeni svoj naslov. To pomeni avtomobil (ki se hitro nadaljuje 80 km/h) in motocikel se premikata v pozitivni smeri.

V nekem trenutku motocikel presega avtomobil in otrok, ki gre na zadnji sedež avtomobila.

Za pridobitev odgovora otrok ponovno uporabi odnose relativnega gibanja:

V_Pb= V_Pa + V_Ab=V_Pa - V_Ba

V_Pb= +100 km/h Yo - 80 km/h Yo = 20 km/h Yo 

Otrok z zadnjega sedeža opazuje, da motocikel napreduje s hitrostjo 20 km/h.

-Vaja rešena

Vaja 1

Motorni čoln prečka reko široko 600 m in teče od severa proti jugu. Hitrost reke je 3 m/s. Hitrost čolna glede na rečno vodo je 4 m/s proti vzhodu.

Vam lahko služi: veje klasične in sodobne fizike

(i) Poiščite hitrost čolna glede na obrežnjo.

(ii) navedite hitrost in smer čolna glede na zemljo.

(iii) Izračunajte čas prehoda.

(iv) Koliko se bo premaknilo proti jugu glede na izhodišče.

Rešitev 

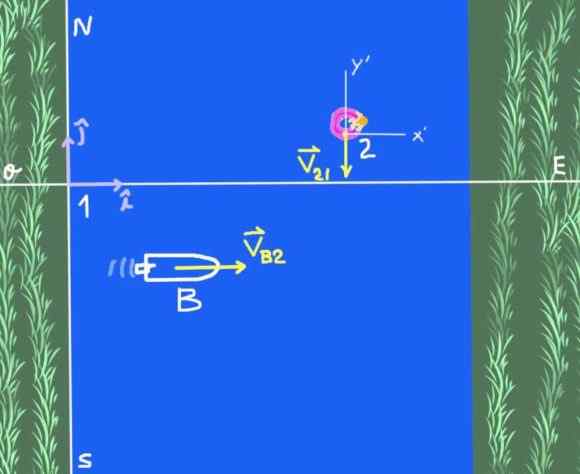Slika 2. Čoln, ki prečka reko (vaja 1). Vir: Self Made.

Obstajata dva referenčna sistema: referenčni sistem solidarnosti na reki, ki ga bomo poklicali 1, in referenčni sistem 2, ki je opazovalec, ki plava na rečni vodi. Predmet študija je čoln B.

Hitrost čolna glede na reko je napisana v vektorski obliki, kot sledi:

VB2 = 4 Yo gospa

Hitrost opazovalca 2 (splav nad reko) glede na opazovalca 1 (na kopnem):

Venaindvajset = -3 J gospa

Želite najti hitrost čolna glede na zemljišče VB1.

VB1 = VB2 + Venaindvajset

Odgovor i

VB1 = (4 Yo - 3 J) gospa   

Hitrost čolna bo prejšnji modul hitrosti:

|VB1| = (42 + (-3) 2) ½ = 5 m/s

Odgovor II

In naslov bo:

θ = Arcan (-¾) = -36,87 ° 

Odgovor III

Čas prehoda čolna je razmerje med širino reke in komponento x hitrosti čolna glede na zemljo.

t = (600m)/(4 m/s) = 150 s 

Odgovor IV

Za izračun premika, ki ga je imel čoln proti jugu, se komponenta in hitrost čolna glede na tla pomnoži s časom prehoda:

d = -3 J m/s * 150 s = -450 J m

Premik proti jugu glede na izhodišče je 450m.

Reference

1. Giancoli, d. Fizika. Načela z aplikacijami. 6. izdaja. Dvorana Prentice. 80-90
2. Resnick, r. (1999). Fizično. Zvezek 1. Tretja izdaja v španščini. Mehika. Continental uredništvo s.Do. od c.V. 100-120.
3. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7. Izdaja. Mehika. Uredniki učenja Cengage. 95-100.
4. Wikipedija. Relativna hitrost. Okreval od: Wikipedia.com
5. Wikipedija. Metoda relativne hitrosti. Okreval od: Wikipedia.com