Vektorji v vesolju, kako graditi, aplikacije, vaje

A vektor v vesolju Vse ga predstavlja koordinatni sistem x, in in z. Skoraj vedno letalo Xy To je ravnina vodoravne površine in os z predstavlja višino (ali globino).

Kartezijanske koordinatne osi, prikazane na sliki 1, razdelite prostor na 8 regij, imenovanih Oktaverji, Analogno s tem, kako seki x - in Letalo razdelite na 4 kvadrante. Nato bomo imeli 1 oktent, 2. ocanto in tako naprej.

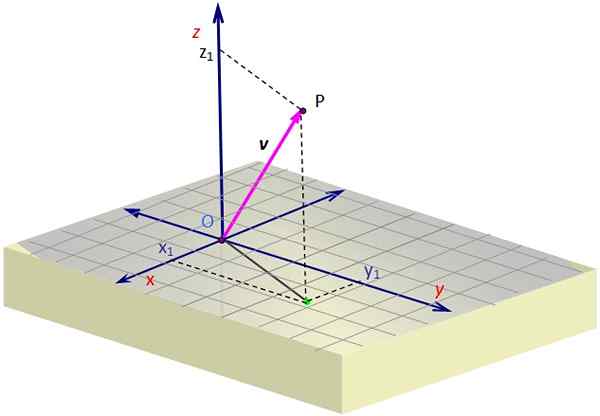
Slika 1. Vektor v vesolju. Vir: Self Made.

Slika 1 vsebuje predstavitev vektorja v v prostoru. Nekatera perspektiva je potrebna za ustvarjanje iluzije treh dimenzij na ravnini zaslona, ​​kar dosežemo z risanjem poševnega pogleda.

Če želite graditi 3D vektor, morate pomagati pikčaste črte, ki določajo koordinate projekcije ali "sence" omrežja v Čez površino X-in. Ta projekcija se začne v O in konča na zeleni točki.

Ko boste tam morali nadaljevati navpično do višine (ali globine), je potrebna glede na vrednost z, Dokler ne pridete do P. Vektor je narisan iz O in konča v P, ki je v primeru v 1. ocantu.

[TOC]

Prijave

Vektorji v vesolju se pogosto uporabljajo v mehaniki in drugih vejah fizike in inženiringa, saj strukture, ki nas obkrožajo, potrebujejo geometrijo v treh dimenzijah.

Vektorji položaja v prostoru se uporabljajo za pozicioniranje predmetov glede na referenčno točko, imenovano izvor Tudi. Zato so tudi potrebna orodja pri navigaciji, vendar to ni vse.

Vam lahko služi: elektromagnetni valovi: Maxwell teorija, vrste, značilnosti

Sile, ki delujejo na strukture, kot so vijaki, nosilci, kabli, oporniki in še več, so vektorska narava in so usmerjene v vesolje. Da bi spoznali njegov učinek, je treba vedeti vaš naslov (in tudi vaše vlogo).

In pogosto je smer sile znana z dvema točkama v vesolju, ki pripada njeni akciji. Na ta način je sila:

F = F ali

Kjer je F velikost ali modul sile in ali Je vektor enote (modul 1), usmerjen vzdolž linije delovanja F. 

3D vektorske zapise in reprezentacije

Preden rešimo nekaj primerov, bo zapis 3D vektorjev na kratko pregledan.

V primeru slike 1 ima vektor V, katerega izvorna točka sovpada z izvorom ali in katerih konec je točka P, koordinate x in z pozitivno, medtem ko koordinira in Je negativno. Te koordinate so: x₁, in₁, z₁, ki so natančno koordinate P.

Če imamo vektor, povezan z izvorom, to je, katerega izhodišče sovpada z O, je zelo enostavno označiti njegove koordinate, ki bodo tiste iz skrajne točke ali P. Za razlikovanje med točko in vektorjem bomo uporabili za najnovejša drzna črka in oklepaje, kot je ta:

v = < x₁, in₁, z₁ >

Medtem ko je točka P označena s oklepaji:

P = (x₁, in₁, z₁)

Druga predstavitev uporablja enotne vektorje Yo, J in k ki določa tri smeri prostora v osi x, in in z oziroma.

Ti vektorji so pravokotni drug na drugega in sestavljajo a Ortonormalna baza (Glej sliko 2). To pomeni, da lahko 3D vektor zapišemo v smislu:

Vam lahko služi: valovito gibanje: značilnosti, vrste valov, primeri

v = v_x Yo + v_in J + v_z k

Koti in režiserice vektorja Ponosa

Slika 2 prikazuje tudi kote režiserjev γ₁, γ₂ in γ₃ kot vektor v oziroma z osi x, in in z. Če poznamo te kote in velikost vektorja, je to popolnoma določeno. Poleg tega kosinus režiserjev izpolnjujejo naslednji odnos:

(cos γ₁)² + (cos γ₂)² + (cos γ₃)² = 1

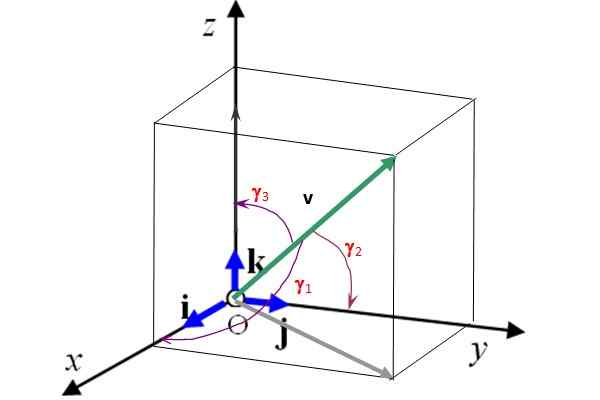Slika 2. Enotni vektorji I, J in K določajo 3 preferencialne smeri prostora. Vir: Self Made.

Rešene vaje

-Vaja 1

Na sliki 2 so γ koti₁, γ₂ in γ₃ kot vektor v OBLIKOV modula 50 z koordinatnimi osi: 75.0 °, 60.0 ° in 34.3. mesto. Poiščite kartezijanske komponente tega vektorja in ga predstavljajte v smislu vektorjev enot Yo, J in k.

Rešitev

Projekcija vektorja v na osi x je v_x = 50 . Cos 75 ° = 12.941. Podobno projekcija v na osi in je v_in = 50 cos 60 ° = 25 in končno na osi z je v_z = 50. cos 34.3. = 41.3. Zdaj v se lahko izrazi kot:

v = 12.9 Yo + 25.0 J + 41.3 k

-Vaja 2 

Poiščite napetosti v vsakem od kablov, ki držijo vedro figure, ki je v ravnotežju, če je teža 30 N.

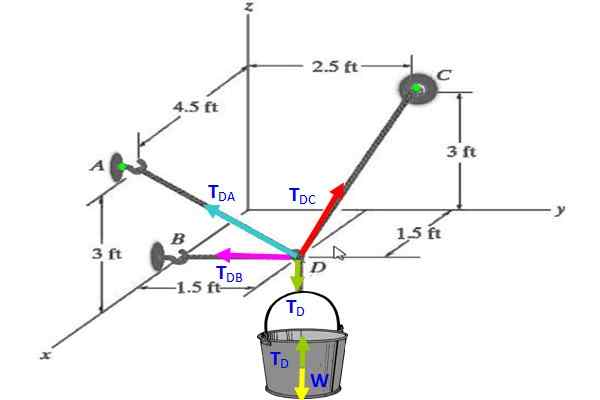Slika 3. Diagram napetosti za vajo 2.

Rešitev

Na vedro shemo prostega telesa kaže na to T_D (zelena) kompenzira težo W (rumena), torej t_D = W = 30 n.

V vozel je vektor T_D  Nato je usmerjena navpično navzdol, nato pa:

T_D = 30 (-k) N.

Če želite vzpostaviti preostale napetosti, morate slediti naslednjim korakom:

1. korak: Poiščite koordinate vseh točk

A = (4.5; 0; 3) (a je na stenski ravnini X-Z)

B = (1.5; 0; 0) (B je na osi x)

Vam lahko služi: naslov (fizično)

C = (0, 2.5, 3) (C je na stenski ravnini in z)

D = (1.5; 1.5; 0) (d je na vodoravni ravnini  X-in)

2. korak: Poiščite vektorje v vsaki smeri, tako da odštejete koordinate konca in začetek

Daje =

DC =

Db =

3. korak: Izračunajte module in vektorje enote

Enotni vektor dobimo z izrazom: ali = r / r, z r (krepko) biti vektor in r (brez krepko) modul omenjenega vektorja.

Da = (3² + (-1.5)² + 3²)^½ = 4.5; Dc = ((-1.5) ² + 1² + 3²)^½ = 3.5

ali_Daje = 4.5 =

ali_DC = 3.5 =

ali_Db =

ali_D =

4. korak: Vse napetosti izražajte kot vektorji

T_Daje = T_Daje ali_Daje = T_Daje

T_DC = T_DC ali_{Dc =}  T_DC

T_Db = T_Db ali_Db = T_Db

 T_D = 30

5. korak: Uporabite stanje statičnega ravnotežja in rešite sistem enačb

Končno se stanje statičnega ravnotežja uporablja za vedro, tako da je vektorska vsota vseh sil na vozlu praznina:

T_Daje + T_DC + T_Db + T_D = 0

Ker so napetosti v prostoru, bo za vsako komponento privedlo do sistema treh enačb (x, in in z) napetosti.

0.67 t_Daje -0.43 t_DC + 0 t_Db = 0

-0.33 t_Daje + 0.29 t_DC - T_Db = 0

0.67 t_Daje + 0.86 t_DC +0 t_Db - 30 = 0

Rešitev je: t_Daje = 14.9 n; T_Daje = 23.3 n; T_Db = 1.82 n

Reference

1. Bedford, 2000. Do. Mehanika za inženiring: statična. Addison Wesley. 38-52.
2. Figueroa, d. Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika.31-68.
3. Fizično. Modul 8: Vektorji. Okrevano od: FRTL.UTN.Edu.ar
4. Hibbeler, R. 2006. Mehanika za inženirje. Statična. 6. izdaja. Continental uredništvo. 15-53.
5. Dodatni kalkulator vektor. Okrevano od: 1728.org